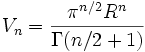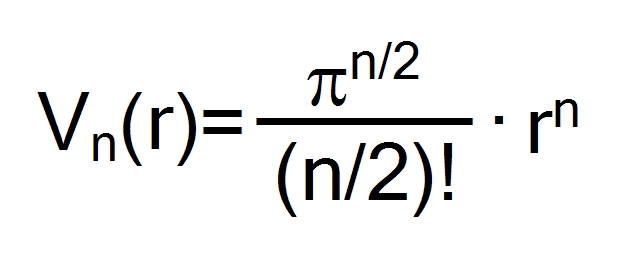canpornpoppy
Diskussionsleiter

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

dabei seit 2007
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Rauminhalt - oder n-dimensionale Volumina!
06.03.2008 um 00:53hi
ich hab mir gerade was überlegt, wo für ich keine antwort weiß (keine sorge, hab die sufu benutzt, sie spuckt auch was aus, allerdings nix was mir hilft)
hmm... wo fang ich an... es geht um volumen bzw. um rauminhalt
das problem welches ich nun habe ist die anzahl der dimensionen im zusammenhang mit dem volumen, denn betrachten wir ein quadrat, dann beträgt das volumen (flächeninhalt) v = a * a = a²
betrachten wir einen hexaeder (würfel), dann beträgt das volumen v = a * a * a = a³
betrachten wir nun ein tesserakt (hyperwürfel), dann v = a4
seht ihr wo das hin führt? für n-dimensionale würfel gilt v = an
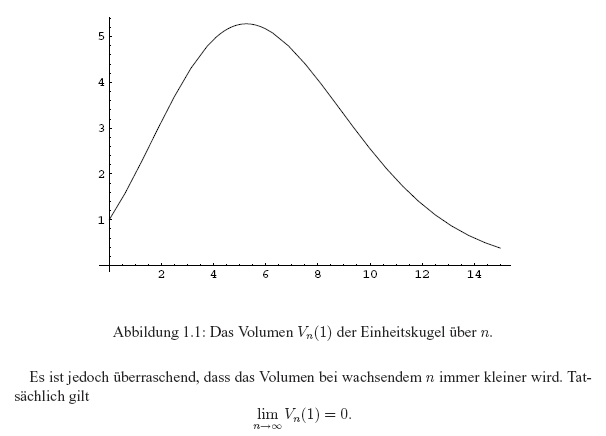
auf gut deutsch, je mehr dimensionen, je mehr "raumangebot" steht zur verfügung, is ja eigentlich logo, ich wird zwar nich meine hand für ins feuer legen aber ich schätze das gilt für so ziemlich alle körper... aber moment! ich hab es zwar heut nich zum ersten mal gelesen, aber dennoch frage ich mich heut, warum! hat die n-dimensionale kugel bei der dimension 5,26 ihren größten rauminhalt... den das volumen strebt bei unendlich vielen dimensionen gegen null!
okay... blabla, gebrochene, unkrumme und 2-stellige dimensionen sind nich wirklich relevant in unserem universum und sind eher mathematischer natur, aber liege ich mit meiner menschlichen vorstellung so falsch? "mehr dimensionen = mehr platz"
ps: ich hätte euch ja nen link gelinkt, allerdings find ich gerad auf die schnelle nix, dachte sowas stand auch mal in der wiki... wenn interesse besteht, ich hab hier noch ein *.pdf rum liegen, da steht auch die formel für das volumen der n-d-kugel drin
hmm... danke ersma im voraus... vllcht is es ja wirklich nur mathematisch, aber ist mit menschlicher logik kaum zu vereinbaren...
ich hab mir gerade was überlegt, wo für ich keine antwort weiß (keine sorge, hab die sufu benutzt, sie spuckt auch was aus, allerdings nix was mir hilft)
hmm... wo fang ich an... es geht um volumen bzw. um rauminhalt
das problem welches ich nun habe ist die anzahl der dimensionen im zusammenhang mit dem volumen, denn betrachten wir ein quadrat, dann beträgt das volumen (flächeninhalt) v = a * a = a²
betrachten wir einen hexaeder (würfel), dann beträgt das volumen v = a * a * a = a³
betrachten wir nun ein tesserakt (hyperwürfel), dann v = a4
seht ihr wo das hin führt? für n-dimensionale würfel gilt v = an
auf gut deutsch, je mehr dimensionen, je mehr "raumangebot" steht zur verfügung, is ja eigentlich logo, ich wird zwar nich meine hand für ins feuer legen aber ich schätze das gilt für so ziemlich alle körper... aber moment! ich hab es zwar heut nich zum ersten mal gelesen, aber dennoch frage ich mich heut, warum! hat die n-dimensionale kugel bei der dimension 5,26 ihren größten rauminhalt... den das volumen strebt bei unendlich vielen dimensionen gegen null!
okay... blabla, gebrochene, unkrumme und 2-stellige dimensionen sind nich wirklich relevant in unserem universum und sind eher mathematischer natur, aber liege ich mit meiner menschlichen vorstellung so falsch? "mehr dimensionen = mehr platz"
ps: ich hätte euch ja nen link gelinkt, allerdings find ich gerad auf die schnelle nix, dachte sowas stand auch mal in der wiki... wenn interesse besteht, ich hab hier noch ein *.pdf rum liegen, da steht auch die formel für das volumen der n-d-kugel drin
hmm... danke ersma im voraus... vllcht is es ja wirklich nur mathematisch, aber ist mit menschlicher logik kaum zu vereinbaren...