Newtonsche Mechanik

Auf Anregungen diverser User hin werde ich die Grundprinzipien der klassischen Physik auf Basis der angewandten Mathematik, speziell der angewandten Analysis, näher erläutern.
Zur besseren Verständlichkeit verzichte ich auf mathematische Beweise und exakte analytische Formulierungen.
Wer überdies Fragen zur reinen Mathematik hat der kann sich gerne an mich wenden.
Ein erstes größeres Ziel ist das Vermitteln der Differential und Integralrechnung anhand physikalischer Beispiele.
Fangen wir an;

Newtonsche Axiome

1. Trägheitsprinzip
Ein Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, solange keine äusseren Einflüsse auf ihn wirken. Die Geschwindigkeit eines solchen sich «frei» bewegenden Körpers ist nach Betrag und Richtung konstant.


2. Beschleunigungsprinzip
Durch einwirkende Kräfte erfährt ein Körper eine Beschleunigung, die der Kraft proportional ist und deren Richtung besitzt: Kraft = Masse * Beschleunigung. (Zu Ehren Newtons wird die Einheit der Kraft 1 N (Newton) ganannt.)


3. Wechselwirkungsprinzip (actio = reactio)
Uebt ein Körper A auf einen Körper B eine Kraft aus (actio), so übt auch B auf A eine Kraft aus, Gegenkraft (reactio) genannt, die entgegengesetzt gleich der ersten Kraft ist.

http://www.bio-chart.com/mm/newton.html

Die Durchschnittsgeschwindigkeit ist die Strecke dividiert durch die Zeit in der die Strecke zurückgelegt wurde; formal: v = s/t

Beispiel: s = 50m, t = 5s
Also v = 50m/(5s) = 10m/s

Aus v=s/t ergibt sich sogleich s = vt;

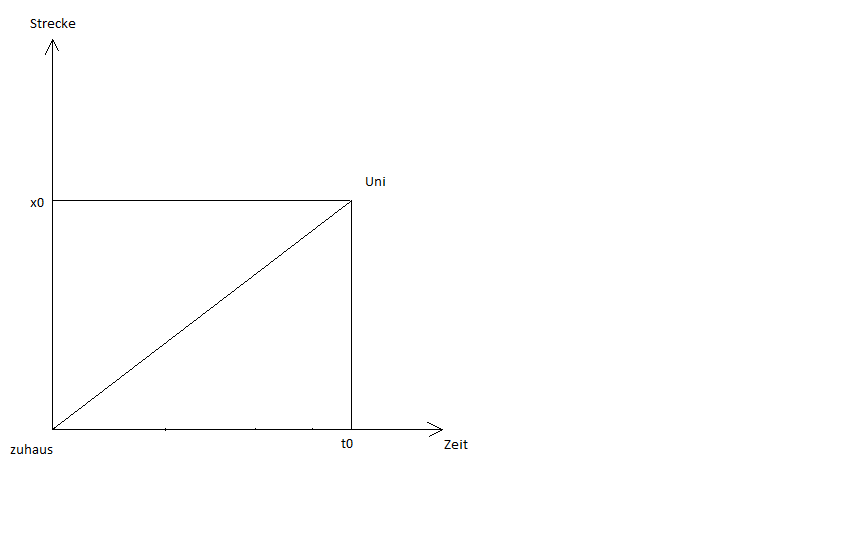
Erfüllt ein Körper die Anforderungen an das erste newtonsche Axiom, so ist Durchschnittsgeschwindigkeit über den betrachteten Zeitraum konstant.
Trägt man das in ein kartesisches Koordinatensystem ein, wobei t die Abszisse (also die horizontale Achse) und s die Ordinate (die vertikale Achsen), ergibt sich eine Gerade.

Wirkt auf einen Körper mit der Masse m eine konstante Kraft F, so gilt: F = m*a. Wobei a hier die Beschleunigung ist. Das ist das zweite newtonsche Axiom.

Was ist eine Beschleunigung ? Eine Beschleunigung ist die Änderung der Geschwindigkeit
v_1-v_0 dividiert durch die Zeit in der diese Änderung stattfand. Also a = (v_1-v_0)/(t_1-t_0)
Also ergibt sich für die Kraft F = m(v_1-v_0)/(t_1-t_0)

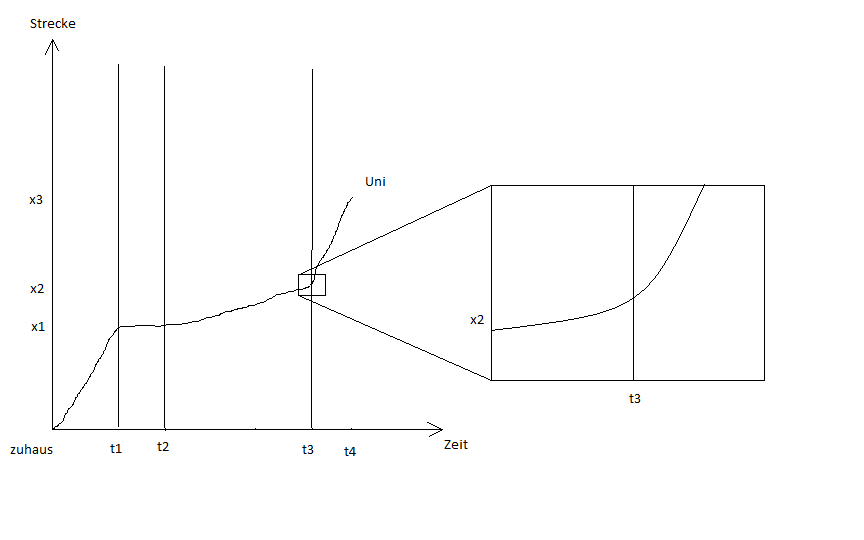
Für Strecken, bei denen v zeitabhängig ist, also es eine Funktion v(t), die zu jedem Zeitpunkt eine Geschwindigkeit zuordnet, gilt s = v*t im Allgemeinen nicht mehr. Es gilt s(t) = 1/2at².

Die Zusammenhänge werden bei der Einführung der eindimensionalen Differentialrechnung klar.

Also beginnen wir mit den Regeln für das differenzieren von Abbildungen der Form f:R->R
R ist hierbei der reelle Zahlenkörper. Was ein Körper genau ist, soll hier außen vor bleiben.

Fangen wir mit der Wiederholung der Ableitungsregeln an;

Seien u(x),v(x) differenzierbare Funktionen mit u:R->R, v:R->R ; V:R->R
Sei µ aus dem reellen Zahlenkörper und x_0 aus dem Intervall [a,b]
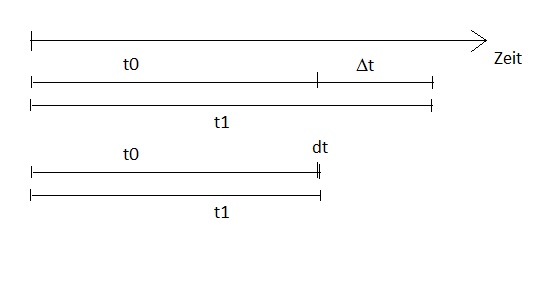
Dann ist die Ableitung definiert als Grenzwert;

lim_[x->x_0]((u(x)-u(x_0)/(x-x_0))

Es gibt noch eine wesentlich "schärfere" Definition; die jedoch eher für die reine Mathematik interessant ist.

d/dx bezeichnet nun die Ableitung von der entsprechenden Funktion nach x.
Statt d/dx kann auch " ' " verwendet werden, also d/dx(f(x)) = f'(x)

d/dx (u(x)+v(x)) = d/dx(u(x)) +d/dx(v(x)), d/dx(µu(x)) = µ d/dx (u(x)) / Summenregel & Linearität
d/dx (u(x)v(x)) = d/dx (u(x)) v(x) + u(x) d/dx(v(x)) / Produktregel
d/dx (V(u(x))) = v(u(x))d/dx(u(x)) / Kettenregel

Es gibt noch weitere Regeln; belassen wir es erstmal dabei...

Beispiel; f(x) = u(v(x))*2x

d/dx (f(x)) = u'(v(x))v'(x)2x+u(v(x))2 = 2(u'(v(x))v'(x)x+u(v(x))

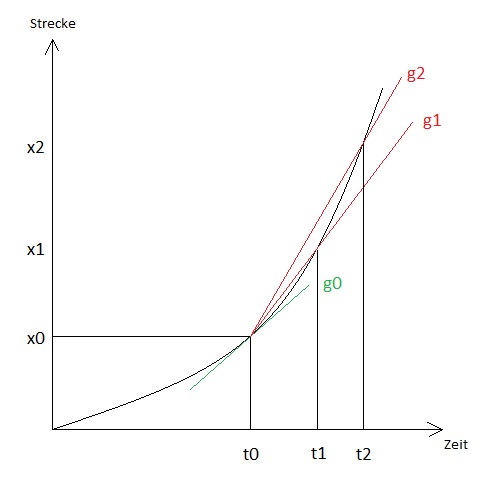
Grafisch ist die Ableitung nach x ausgewertet an der Stelle x_0 die Steigung der Tangente am Punkt P(x_0;f(x_0))

Soweit erstmal...

@mathematiker

Kann Dich nur ermutigen: Mehr davon! Es ist wichtig, dieses Wissen in einer nötigen (mathematischen) Tiefe vermittelt zu bekommen. Ich werde mir dies auch mal näher zu Gemüte führen und nach und nach hoffentlich auch vollends verstehen.

Ob Dein Vorhaben hier im Forum allerdings Erfolg haben wird, weiß ich nicht ... die meisten interessieren sich nur für die "groben" Ergebniße.

@mathematiker
@Mr.Dextar
Ich glaube nicht, dass das irgend eine der angesprochenen Personen versteht - viel zu formal. Kann keiner was mit anfangen. Die Einschränkungend der Schreibweise trägt noch dazu bei.

@mathematiker
Wenn Du es wirklich erklären willst, verzichte auf die Formelsprache und versuche umgangssprachlich zu erklären, was z.B. ne Funktion oder eine Ableitung ist und was sie bedeutet. Geht so nämlich auch :) Ist nur nicht so bequem wie Skriot abschreiben :)

Ich finde diesen Thread auch sehr interessant! Ich persönlich denke aber im Gegensatz zu @Mr.Dextar , das für die Mehrheit eher die Ungereimtheiten interessant sind.
SH. Wer sich in ein Themengebiet einarbeitet kommt irgendwann an Grenzen, oder an Dogmen ZB:

mathematiker schrieb:1. Trägheitsprinzip
Ein Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, solange keine äusseren Einflüsse auf ihn wirken. Die Geschwindigkeit eines solchen sich «frei» bewegenden Körpers ist nach Betrag und Richtung konstant.

Dieses Prinzip ist doch für relativ kurze Distanzen von Interesse und von Gültigkeit!

Und selbst im Mikrokosmos ist es fraglich, ob es Gültigkeit hat!

@Shotokan

Shotokan schrieb:Dieses Prinzip ist doch für relativ kurze Distanzen von Interesse und von Gültigkeit!

Und selbst im Mikrokosmos ist es fraglich, ob es Gültigkeit hat!

mathematiker schrieb:Ein Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, solange keine äusseren Einflüsse auf ihn wirken

Kann man umformulieren zu;

Ein Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, genau dann, wenn keine äusseren Einflüsse auf ihn wirken

Also gilt;
"Ein Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung" => "Es wirken keine äußeren Einflüsse auf den Körper"

"Es wirken keine äußeren Einflüsse auf den Körper" => "Ein Körper beharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung"

Die Aussagen sind äquivalent (bikonditional), womit klar ist, wann es Gültigkeit hat. Unter anderem spielt die Distanz keinerlei Rolle.

@FrankD

FrankD schrieb:Wenn Du es wirklich erklären willst, verzichte auf die Formelsprache und versuche umgangssprachlich zu erklären, was z.B. ne Funktion oder eine Ableitung ist und was sie bedeutet. Geht so nämlich auch :) Ist nur nicht so bequem wie Skriot abschreiben :)

Wenn man es wirklich jemanden erklären will, der es richtig verstehen will, sollte man eigentlich mit mathematischer Logik, axiomatischer Mengenlehre und Kategorientheorie anfangen, also mit Grundlagenmathematik.
Da das auf wenig Freude stoßen würde, vermittelt man eben erst einmal die naive Mengenlehre, auch auf das habe ich hier verzichtet.
Es dreht sich doch nur um angewandte Mathematik, was die Ableitung grafisch bedeutet, habe ich zudem in einfachen Worten, mathematisch unpräzise, erläutert.

mathematiker schrieb:Grafisch ist die Ableitung nach x ausgewertet an der Stelle x_0 die Steigung der Tangente am Punkt P(x_0;f(x_0))

Die Steigung und Tangente kennt man aus der Mittelstufe.

Kommen wir zu einigen formalen Zusammenhängen;

s(t) = 1/2at²; v(t) = at;

Zuvor führen wir noch unbewiesen die Potenzregel ein;

f:R->R,
t sei aus R und n aus dem Körper der natürlichen Zahlen.
hat f(t) die Form; f(t) = t^n
dann gilt f'(t) = nt^(n-1)

Differenziert man s(t) nach dem Argument t, erhält man mit der Produktregel;

d/dt (s(t)) = d/dt (1/2at²) = at = v(t)

Die Ableitung der Strecke nach der Zeit ist also die Geschwindigkeit.
Grafisch ist die Steigung der Tangente am Punkt P(t_0, s(t_0)) also die Momentangeschwindigkeit

Die Ableitung der Momentangeschwindigkeit nach der Zeit ist die Beschleunigung; d/dt (v(t)) = a
Es gilt;

s(t) = 1/2 t s'(t)

Eine solche Gleichung, die die Ableitung(en) einer Funktion mit der Funktion selbst ins Verhältnis setzt, nennt man Differentialgleichung, dazu später mehr.

@FrankD


Ich bin kein Physiker, Ingenieur oder Naturwissenschaftler, wenn Du konkrete Verbesserungsvorschläge hast, nur zu :)

Weiter geht's,

Wir führen nun den Begriff der Folge ein, um später Reihen zu motivieren, die für gewisse physikalische Überlegungen von Nöten sind.

Zuerst definieren wir das Bild einer Abbildung f:X->Y

im(f) := {y e Y; ∃x e X : y = f(x)}

In Worten ist das einfach die Teilmenge der Zahlen aus Y, auf die f die Elemente aus X tatsächlich abbildet.

Unter einer Folge versteht man eine Abbildung der Form f:N ->M, aus den natürlichen Zahlen N in eine Menge M.

Beispiel;
Sei nun n aus N und M die reellen Zahlen R.
f_n = (-1)^n
Also ist das Bild von M die Menge im(f) = {1,-1}

Soweit Fragen ?

@mathematiker
Wen möchtest Du denn mit dem Thread erreichen?

Wenn das ein Einführungsthread für alle sein soll, dann vermute ich, dass Du mit den mathematischen Formulierungen schon zu weit gehst.

Wenn die Formeln unübersichtlich werden könnte man einen Tex-editor im Netz benutzen, wie
http://www.zahlen-kern.de/editor/

Das kann man dann als Bild einfügen, laut Autor sollen die links dauerhaft gespeichert werden


Edit: die Farbe wird in der Formel mit \color{white} geändert

@mathematiker

das was du da vorhast (also den Leuten hier was beibringen) ist sehr löblich wie ich finde.
allerdings denke ich nicht, dass es in dieser Art und Weise Sinn macht.

Für jemanden der wenig Ahnung von der Materie hat ist es zu mühselig zu verstehen was du da schreibst. Die Tatsache, dass es keine Bilder oder schön dargestellte Formeln gibt hilft auch nicht weiter.

Das Thema ist schon trocken genug wenn man es in der Schule versucht zu lernen, wo dir es jemand aktiv versucht zu vermitteln, aber ein Selbststudium ist nochmal trockener.

Die Leute die Interesse haben sich das beizubringen sollten sich passende und gute Bücher ausleihen.
Diese Bücher sind dann auch didaktisch richtig aufgebaut und können durchaus motivierend sein.

@trololol
@Zotteltier


Naja, es ist wahrscheinlich zwecklos. Die Leute wollen lieber über Wurmlöcher, Quanten, Zeitreisen,... etc debattieren, obgleich kaum einer mathematisch argumentiert. Das ist in der Regel zwar sinnloses Geschwafel, aber an sich ganz amüsant.
Genauso gut könnte ein Blinder über Farben reden.

soll nicht blöd klingen, aber ich dachte bisher, dass das Forum hier nur dafür da ist. "Mit gefährlichem Halbwissen Sachen widerlegen die seit 100 Jahren bewiesen sind"

@trololol
Den Eindruck habe ich in letzter Zeit auch immer stärker.

Plus "versuchen, wie viele logische und argumentative Fehler man in einen Beitrag rein bekommen kann".

@mathematiker

mathematiker schrieb:Naja, es ist wahrscheinlich zwecklos.

Nur nicht den Mut verlieren. Die Idee für den Thread finde ich gut. Ich wollte nicht in Frage stellen ob der Thread an sich, sondern ob die Herangehensweise didaktisch sinnvoll sind.

Wenn ich ein breites Publikum damit erreichen will, sollte zunächst weniger die mathematische Strenge, sondern die ausführliche anschauliche Erklärung angestrebt werden, um dann auf dieser Basis auf die mathematisch saubere Formulierung hinzuarbeiten.

Am Beispiel der Ableitung werde ich mal versuchen ob ich das hinbekomme, wie ich mir das vorstelle, könnte aber etwas dauern.

@Zotteltier


Hallo tufkaz,

Ich würde mich freuen, wenn Du dich hier ein wenig einbringst. Mal schauen, ob der Thread mehr Resonanz erhält, wenn man das Thema anders vermittelt. Ich kann das leider nur so.

Und jetzt mal ein reelles Beispiel. :-)
Ein Rennfahrer fährt ein Rennen über zwei Runden.
Am Ende ersten Runde wird eine Durchschnittsgeschwindigkeit von 100 km/h gemessen.
Wie schnell muss er die zweite Runde fahren, damit er am Ende des Rennens eine Durchschnittsgeschwindigkeit von 200 km/h gefahren ist?

Ich werde auf einem relativ niedrigen Level einsteigen, in der Hoffnung möglichst viele dabei mitnehmen zu können.

Also wir wollen uns das Konzept der Ableitung zunächst am Beispiel der Geschwindigkeit verdeutlichen, ähnlich wie @mathematiker da schon angefangen hat.

Zunächst eine kleine Einführung zur Geschwindigkeit ohne Differentialrechnung.

Als Beispiel will ich meinen damaligen Weg zur Uni beschreiben. Das ging eigentlich immer schön geradeaus an einer Hauptstraße entlang, keine Kurven und keine Steigung, es ist also erstmal nur eine Richtung von Belang. Wir müssen uns erstmal nicht darum kümmern, dass Geschwindigkeiten auch eine Richtung haben die man beachten muss.

Eine Geschwindigkeit gibt an wieviel Strecke ich in einer bestimmten Zeit zurücklege.

Für meine Fahrt zur Uni könnte ich also die Strecke von meiner Wohnung zur Uni messen und feststellen wieviel Zeit ich für diese Strecke benötige.

Hierbei steht 't' für die Zeit, die Strecke bezeichne ich mit 'x' (Tensor hat sie mit 's' bezeichnet, ich bleibe aber bei 'x', da ich das so schon in den Bildern bezeichnet habe).

Das sähe dann in einem Diagramm etwa so aus:


Bild 1

Wenn ich meine Wohnung in den Koordinatenursprung lege, dann ist die Geschwindigkeit einfach x0 geteilt durch t0. Das ist aber genauso die steigung der eingezeichneten Geraden.

Die Geschwindigkeit ist also die Steigung einer Kurve im Orts-Zeit-Diagramm.

Genaugenommen muss ich für die Geschwindigkeit eine Differenz der Strecken und Zeiten nehmen, so wie ich für die Messung der Strecke meinen Tachostand vor der Fahrt aufschreibe und meinen Tachostand nach der Fahrt. Dasselbe gilt für die Uhrzeit.

Gleichung 1


'v' ist wie üblich eine Geschwindigkeit. Das Dreieck ist das große griechische Delta, das benutzt man um zu zeigen, dass eine Differenz gebildet wird. Die 'x' sind meine Tachostände und die 't' meine Uhrzeiten.

Wenn ich meinen Tacho auf 0 stelle und eine Stoppuhr benutze, dann werden x_Anfang und t_Anfang 0 und ich rechne so wie oben beschrieben. Damit setze ich dann sozusagen meine Wohnung in den Koordinatnurspung. ;)

Wie ich in der Gleichung schon angedeutet habe ist die Geschwindigkeit nur eine mittlere Geschwindigkeit über den betrachteten Zeitraum, ich werde während der Fahrt sicher nicht durchgehend exakt eine Geschwindigkeit beibehalten.

Eine etwas detailliertere Darstellung habe ich in Bild 2 aufgestellt.


Bild 2

Der Start- und Zielpunkt ist in Bild 2 und Bild 1 der Gleiche allerdings ist in Bild 2 etwas genauer zu sehen, wie die Fahrt aussieht.

Zunächst fahre ich recht schnell los. Meine Geschwindigkeit ist groß also ist die Kurve im Bild relativ steil (im Bild der Abschnitt von 0 bis t1). Dann komme ich an die erste Ampel an der ich normalerweise festhänge, die Geschwindigkeit ist 0 und die Kurve verläuft parallel zur Zeitachse (t1 bis t2). Da ich weiß wie die Ampeln geschaltet sind fahre ich danach eher langsam, die Kurve ist eher flach (t2 bis t3). Wenn ich die zweite Ampel passiert habe trete ich nocheinmal richtig in die Pedale, die Kurve wird wieder steil (t3 bis t4).

Ich könnte jetzt wieder für jeden Teilabschnitt die mittlere Geschwindigkeit mittels Gleichung 1 bestimmen. ich muss dann für die Anfangs- und Endzeiten die 't' und 'x' aus Bild 2 einsetzen. Damit wird meine Beschreibung meiner Fahrt schon wesentlich genauer.

Diese mittlere Geschwindigkeit ist für die Abschnitte selbst schon ganz gut, auf einem geraden Abschnitt kann man eine Geschwindigkeit halten. Interessant werden jetzt die Grenzbereiche. Wenn ich einfach die mittleren Geschwindigkeiten nehme und die dazugehörigen Geraden "aneinanderklebe", dann bekomme ich an der Grenze einen Knick. Das kann so nicht richtig sein, da das bedeuten würde, dass ich in einem Moment z.B. 15 km/h fahre und im nächsten Moment urplötzlich 25 km/h. Erfahrungsgemäß muss ich beschleunigen und das benötigt Zeit.

Graphisch habe ich das in Bild 2 schon mit dem Bildausschnitt dargestellt. Der Übergang von einer Geschwindigkeit zur nächsten muss stetig sein. Aber was ist jetzt die Geschwindigkeit einer solchen Kurve? Oder anders ausgedrückt, da die Geschwindigkeit die Steigung dieser Kurve ist, was ist die Steigung so einer Kurve?

Jetzt kommt endlich Newton (und Leibniz) ins Spiel.

Da dass jetzt schon eine Menge war mach ich erstmal eine kleine Pause bevors eigentlich spannend wird. Ist doch auch ein schöner Cliffhanger :D

Mein letzter Post endete damit, dass ich die Steigung einer gekrümmten Kurve bestimmen wollte.

Wenn man noch einmal auf den kleinen Bildausschnitt in Bild 2 schaut, dann ist die Steigung links von t3 kleiner als bei t3 und rechts davon größer. Wir veranschaulichen das noch etwas anders.


Bild 3

Im Bild 3 soll g0 die Gerade mit der Steigung der Kurve im Punkt (t0,x0) sein. Lege ich jetzt eine Gerade durch die Punkte (t0,x0) und (t2,x2), also g2, dann fällt auf, dass diese noch deutlich steiler als die gesuchte Gerade ist. Mache ich das Ganze mit (t0,x0) und (t1,x1), erhalte also g1, dann ist die Steigung schon deutlich flacher und nähert sich g0 an. Ich benötige ein t, welches noch dichter an t0 liegt. Am besten so dicht wie möglich, ohne dass t1=t0 wird.

Die Differenz zwischen t0 und t1 muss also möglichst klein, also fast aber nicht ganz 0 werden.

Ich habe versucht das in Bild 4 zu verdeutlichen.


Bild 4

Mathematisch sagen wir, wir lassen die Differenz gegen 0 gehen, oder als Formel:



Wie schon in Bild 4 zu sehen, benennen wir das Ganze nicht mehr mit dem großen griechischen Delta sondern mit einem kleinen 'd'.

Wenn also die Differenz sich 0 nähert dann nähert sich die Steigung, und damit die Geschwindigkeit, einem bestimmten Wert. Wir nehmen noch einmal Gleichung 1 und bilden den sogenannten Grenzwert, der mit 'lim' bezeichnet wird. Das steht für 'limes', was das lateinische Wort für Grenzwall ist.

Nochmal in Worten:
Die Geschwindigkeit zum Zeitpunkt t0 ist der Grenzwert der Gleichung 1 wenn wir (t1-t0) gegen 0 gehen lassen. Und als Formel:

Gleichung 2


In Gleichung 2 ist bereits angedeutet, dass der Ort eine Funktion (den Funktionsbegriff werde ich vielleicht später definieren) der Zeit ist, dadurch ausgedrückt, dass dort x(t0) steht (gelesen 'x von t0').

Wenn ich diese Funktion kenne dann kann ich mit Gleichung 2 auch die Geschwindigkeit ausrechnen. Als Beispiel wollen wir x=t² versuchen.

x(t0) bedeutet nun nichts anderes, als dass ich t0 für t einsetze. Man schreibt

x(t0)=t0² und
x(t0+dt)=(t0+dt)²=t0² + 2 t0 dt + dt² (binomische Formel)

Da dt schon sehr sehr klein ist wird sein Quadrat nochmal wesentlich kleiner hat also keinen Einfluss auf das Ergebnis. Das t0² fällt wegen der Differenz heraus und es bleibt

dx=2 t0 dt |/dt (wir teilen durch dt)

und wir erhalten



Wir haben soeben eine Funktion abgeleitet bzw. differenziert, und damit die Momentangeschwindigkeit an einem Beispiel berechnet.

So und jetzt warte ich erstmal auf feedback.

@Zotteltier


Ich finde Deinen Text lesenswert, hoffentlich wird Du eine entsprechende Resonanz von den angesprochenen Personen erhalten. Bis jetzt schein sich das Interesse in Grenzen zu halten, wobei Deine Einführung wirklich jeder verstehen müsste, wer das nicht versteht, hat in der Physik nichts verloren.

-----
Vielleicht war das mit den "Folgen" ein wenig zu hoch gegriffen. Bleiben wir bei der Physik.

Das newtonsche Gravitationsgesetz



F die Gravitationskraft die auf die beiden Massen m_1 und m_2 wirkt.
r der Abstand der Massenmittelpunkte. Man geht davon aus, dass die Körper der Kugelsymmetrie genügen.
G ist die sogenannte Gravitationskonstante, eine universelle Konstante.
Die Gravitationskraft die auf 2 Körper wirkt wird also von Deren Abstand und Masse festgelegt.
Die Formel ist aus zweierlei Gründen nur bedingt korrekt. Zum einem muss explizit eine Kugelsymmetrie vorliegen, zum anderen darf die Raumzeit Krümmung, die die Massen (und allgemein jede Form von Energie) verursachen, nicht allzu signifikant sein.

Auf der Erdoberfläche gilt sogar der noch einfachere Zusammenhang:

F = mg, wobei m die Masse des Objektes und g die Feldstärke der Gravitation ist.

Die beiden Formeln scheinen sich zu widersprechen, mit einer "Reihenentwicklung" der newtonschen Formel kann jedoch gezeigt werden, die wesentlichen Ideen bestehen darin die Formel



umzuschreiben zu



und dann nach kleinen weiteren Umformungen in eine Potenzreihe umzuwandeln

wobei r_0 hier der Radius des kugelsymmetrischen Körpers, in diesem Fall der Erde und h die Höhe über der Erdoberfläche ist.

Gm_1/r_0² ist gerade die Feldstärke g des Gravitationsfeldes, der hintere Term



ist ein Korrekturterm. Für h = 0





Erinnern wir uns, r_0 ist der Radius der Erde, bringen wir nun F = mg und F = m_1m_2G/(r_0)² in Einklang: m = m_1 also; F = m_1g = m_1m_2G/(r_0)²

g ist also gerade m_2G/(r_0)²,



bzw:



Ist ein allgemeinerer Ausdruck, des Gravitationsgesetzes, für den Fall, dass die Feldstärke nicht als homogen angenommen werden kann.

mathematiker schrieb am 11.08.2013:Es gibt noch eine wesentlich "schärfere" Definition; die jedoch eher für die reine Mathematik interessant ist.

d/dx bezeichnet nun die Ableitung von der entsprechenden Funktion nach x.
Statt d/dx kann auch " ' " verwendet werden, also d/dx(f(x)) = f'(x)

d/dx (u(x)+v(x)) = d/dx(u(x)) +d/dx(v(x)), d/dx(µu(x)) = µ d/dx (u(x)) / Summenregel & Linearität
d/dx (u(x)v(x)) = d/dx (u(x)) v(x) + u(x) d/dx(v(x)) / Produktregel
d/dx (V(u(x))) = v(u(x))d/dx(u(x)) / Kettenregel

Es gibt noch weitere Regeln; belassen wir es erstmal dabei.

Puh, da musste ich mich erstmal wieder in die Produktregel und Kettenregel einlesen...
Aber ist ja wie Fahrrad fahren...:D

-> http://produktregel.com/

@mathematiker

ich muss gestehen, ich habe deinen letzten Beitrag nicht verstanden. Also den Sinn nicht.

mir wird nicht klar, was du mit dem Beitrag zeigen willst. Wird hier etwas bewiesen? Wird hier etwas hergeleitet?

Genauere Kritik:

1. Du solltest, bevor du etwas schreibst, eine gewisse Motivation geben, das was jetzt kommt verstehen zu wollen. Beschreibe zum Beispiel was man mit dem Wissen Berechnen könnte oder Welche Zusammenhänge mit dem Wissen verständlich werden.

2. Du schreibst die Formel "F=mg" und "F=G*m_1*m_2/r^2" würden sich widersprechen. Und fängst an die Sache mit Potenzreihen zu erklären??
Warum nicht: für "m_1" die Masse der Erde einsetzen für "G" die Gravitationskonstante und für "r" den Radius der Erde. Wenn man das ausrechnet kommt man auf "F=m_2*9,81m/s^2". Jetzt nennt man "m_2" einfach nur "m" und fürs "9,81m/s^2" gibts auch die Abkürzung "g". Schon hat man "F=m*g"

3. Du benutzt Potenzreihen ohne zu sagen warum und wie man sie überhaupt benutzt.

4. Ich versteh echt nicht was die Ausführung mit den Potenzreihen soll. Du nimmst einen ausdruck, modifizierst ihn (r=r_0+h), machst daraus eine Potenzreihe (ohne zu erklären warum und wie), setzt h=0 nur um wieder das rauszubekommen was du gehabt hättest, wenn du von Anfang an h=0 gesetzt hättest. Dieser Ausdruck ist aus irgendeinem Grund wieder exakt der selbe mit dem du Angefangen hast.

Bitte erkläre dich!!

PS: wie zietiert man in diesem Forum?

@trololol

Vorweg;

Zitieren:

mathematiker schrieb:Text

Links neben den Beitragsfenster findest Du einen kleinen unterstrichenen Text "Zitieren".
Statt "Text " fügst Du den zu zitierenden Text ein.

Zum eigentlichen Thema schreibe ich später oder eher Morgen

@mathematiker

mathematiker schrieb:Links neben den Beitragsfenster findest Du einen kleinen unterstrichenen Text "Zitieren".
Statt "Text " fügst Du den zu zitierenden Text ein.

kann man auch hinzufügen, wen man zitiert hat?

Wie Du siehst geschieht dies automatisch ;)

das ist ja Zauberei!!!