Quantenkommunikation

JokerClz schrieb:Sie werden absorbiert und heizen den Filter auf

Nur zum Teil vielleicht, wenn ich @pluss´s Beitrag zwischen uns richtig verstehe.

@pluss
Ich sag ja, rechnerisch ist es klar, aber eben nicht anschaulich. Wenn zwei hintereinander gestellte Filter kein Licht durchlassen, dann würde ich nicht erwarten, das ein dritter Filter - dazwischen platziert, ohne das bei den zwei ursprünglichen Filtern etwas geändert wird - dafür sorgt, dass durch die nun drei Filter Licht hindurch kommt.

Bei allen anderen Filtern die ich mir vorstellen kann, ist es nicht so. Beispielsweise Farbfilter, oder auch ein Sieb. Dort gilt immer, dass bei Hintereinanderreihung von mehreren Filtern das Ergebnis kleiner oder maximal gleich bleibt, im Vergleich zu wenigeren Filtern.

Abstraktes Beispiel: Zahlenfilter.
Nimm als „Eingabe“ die natürlichen Zahlen.
Filter 1: nur gerade Zahlen
Filter 2: nur durch 5 teilbare Zahlen
Filter 3: nur Zahlen die die Ziffer 7 enthalten

Jeder dieser Filter bewirkt, dass weniger Zahlen durchkommen, egal in welcher Anordnung.
Bei den Polfiltern kommt es aber auf die Reihenfolge an, und es gibt Konstellationen, bei der ein in der Mitte platzierter Filter dazu führt, dass mehr Licht durchkommt, als wenn der Filter fehlen würde.
(Ich hoffe das war einigermaßen verständlich ausgedrückt.)

JokerClz schrieb:Abstraktes Beispiel:

Dein Vergleich hinkt.

Wenn nicht polarisiertes Licht auf einen Polfilter trifft, passiert es vollständig den Filter. Das austretende Licht ist dann lediglich polarisiert, aber es gilt I_0=1. Passiert dieses Licht einen weiteren Polfilter mit \alpha =\not 90°, hat das Licht zwar eine dem Winkel \alpha entsprechend geringere Intensität ( I=I_0 \cdot cos^2 \left (\alpha \right ) ), passiert aber den Polfilter, allerdings mit einer neuen, dem Winkel entsprechende Polarität.

Das lässt sich mit beliebig vielen Polfiltern wiederholen. Solange der folgende Polfilter \alpha =\not 90° hat, nimmt lediglich die Intensität immer weiter ab.

@pluss
Dann nimmst du an, dass ein Polfilter ein Photon verändert, quasi die Polarisation „dreht“?

pluss schrieb:Wenn nicht polarisiertes Licht auf einen Polfilter trifft, passiert es vollständig den Filter. Das austretende Licht ist dann lediglich polarisiert, aber es gilt

I0=1I_0=1I0​=1

Ist das richtig?
oder eher dies:


Passiert unpolarisiertes Licht einen idealen linearen Polarisationsfilter, so halbiert sich seine Intensität.

pluss schrieb:

delta.m schrieb:Ist das richtig?
oder eher dies:

Im Kontext passt die obere Aussage schon. Es ging ja insbesondere um den Verlust an Intensität in Bezug auf den Drehwinkel der Polarisationsfilter. Da macht es Sinn die Intensität des erstmalig Polarisierten Lichts mit I_0=1 zu definieren.
Da hätte ich mich gestern sicherlich genauer ausdrücken sollen, sorry für das stiften der Verwirrung.

Bei unpolarisierten Licht ist das Ergebnis ja, unabhängig vom Drehwinkel des Polfilters, immer I= \frac {I_0}{2} nach dem durchlaufen.

pluss schrieb:Im Kontext passt die obere Aussage schon. Es ging ja insbesondere um den Verlust an Intensität in Bezug auf den Drehwinkel der Polarisationsfilter. Da macht es Sinn die Intensität des erstmalig Polarisierten Lichts mit I0=1I_0=1I0​=1 zu definieren.
Da hätte ich mich gestern sicherlich genauer ausdrücken sollen, sorry für das stiften der Verwirrung.

Bei unpolarisierten Licht ist das Ergebnis ja, unabhängig vom Drehwinkel des Polfilters, immer I=I02I= \frac {I_0}{2}I=2I0​​ nach dem durchlaufen.

Ist aber auch verwirrend, es macht ja den von @JokerClz beschriebenen Eindruck dass die Polarisation geändert wird. Damit komme ich auch noch nicht so klar.

mojorisin schrieb:Überlagerungszustände sind normal nicht stationär, d.h. Sie ändern sich mit der Zeit. Reine Zustände hingegen sind stationär. Ich kann das am Freitag mal genauer erklären, wenn ich wieder zuhause bin.

Ich möchte noch kurz etwas zum Thema Zustand in der Physik sagen. Das Konzept des Zustands ist eines der wichtigsten in der Physik sowohl in der klassischen Physik als auch in der Quantenmechanik. Über das Konzept des Zustandes kann man meiner Meinung nach am einfachsten die Brücke zur QM schlagen und auch die Unterschiede zwischen QM und klassicher Physik am Besten verstehen.

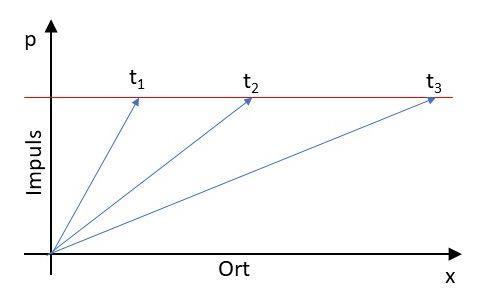
In der klassischen Physik können wir anhand des Zustandes das gesamte betrachtet physikalische System beschreiben. Fangen wir mit etwas ganz einfachem an, einem massebehaftets punktförmiges Modellobjekt das sich nur entlang einer Achse bewegen kann. In der klassischen Physik ist der gesamt Zustand beschrieben mit der Orts- und der Impulsinformation. Der Zustandsvektor gibt uns jetzt zu jedem Zeitpunkt an wo sich das Objekt befindet und mit welcher Geschwindigkeit.



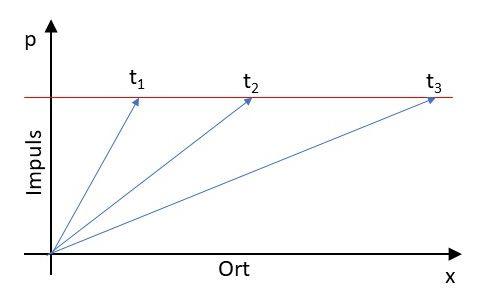
In blau sehen wir den Zustandsvektor zu verschiedenen Zeiten. Der Impuls eines Teilchens bleibt ohne Krafteinwirkung immer gleich und da die Bewegung erhalten bleibt ändert sich der Ort zunehmend. Entscheidend ist hier in der klassischen Physik z.B. das der Ort und der Impuls des Teilchens immer genau messbar sind. In diesem Beipiel sind unendlich viele Zustände möglich, da der Ort sowie Impuls kontinuierlich ist, d.h. es gibt unendlich viele Möglichkeiten wo sich das Teilchen aufhalten kann als auch unendlich viele Möglichkeiten werlchen Impuls das Teilchen haben kann.

Ein anderes Beipiel für einen Zustand der diskret ist, wären die beiden Seiten einer Münze nach dem Wurf. Es gibt dann den Zustand Kopf oder Zahl. Das zugehörige Phasendiagram sieht so aus:



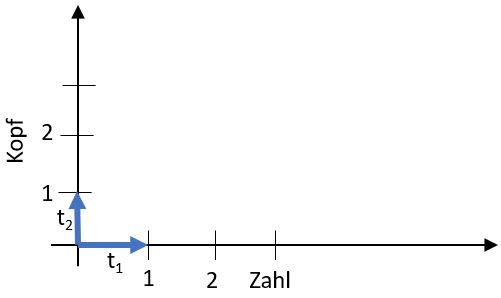
Es gibt nur zwei erlaubte Zustände: 1 Kopf oder 1 Zahl. Es gibt z.B. kein Zustand 2 Kopf oder gar 2 Kopf 1 Zahl. FOlgender Zustand ist also nicht möglich:



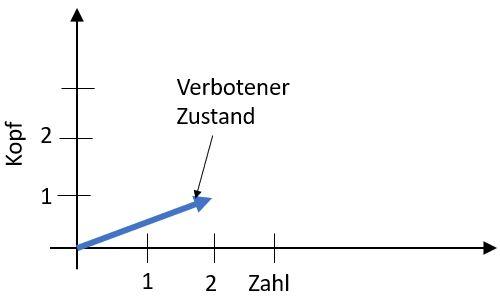
Diesen Zustand gibt es einfach nicht.

In der QM geht es nun genau um solche Zustände. Der Trick is nun das wir nur bestimmte Zustände messen können (Die sogenannten Basiszuständen, in dem Beipiel sind die Basiszustände Kopf und Zahl). Nehmen wir nun nochmal das Münzbeispiel und nehmen wir an das das nun ein quantenmechanisches System sei. Dazu folgendes Bild mit dem blauen Zustandsvektor:




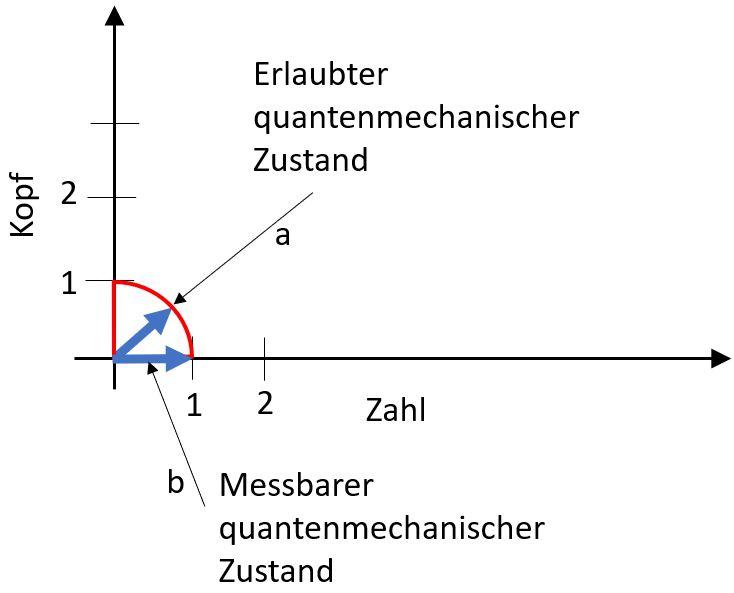
In der QM sind Überlagerungszustände erlaubt, d.h. die Münze kann halb Zahl halb Kopf sein (wie der blaue Vektor von Zustand a im Bild), oder sonst eine Kombination (solange der Zustand normiert ist, sprich der Pfeil die Länge 1 hat.) Wichtig: Messbar sind solche Zustände nicht. Nehmen wir eine Messung vor springt der Zustand entweder auf Kopf oder Zahl, wie der Zustandsvektor b im Bild zeigt.

Bei der Polarisation von Photonen ist es genau dasselbe. Unpolarisierte Photonen sind in einem Übnerlagerungszustand aus den möglichen Basis polarisationszuständen. Passieren sie nun einen Polfilter, findet eine Messung statt und die nehmen einen Baisizustand ein (der berühmte Kollaps der Wellenfunktion). Ist einmal der Basiszsutand erreicht verändert sich dieser nichtmehr (in einem ungestörten System).

Ich hoffe fürs erste helfen diese Erklärungen, aber ich freue mich das auch zu diskutieren.

JokerClz schrieb:Ich sag ja, rechnerisch ist es klar, aber eben nicht anschaulich. Wenn zwei hintereinander gestellte Filter kein Licht durchlassen, dann würde ich nicht erwarten, das ein dritter Filter - dazwischen platziert, ohne das bei den zwei ursprünglichen Filtern etwas geändert wird - dafür sorgt, dass durch die nun drei Filter Licht hindurch kommt.

JokerClz schrieb:Dann nimmst du an, dass ein Polfilter ein Photon verändert, quasi die Polarisation „dreht“?

das wuerde mich auch interessieren, oder ist die frage "so" nicht beantwortbar?

JokerClz schrieb:@pluss
Dann nimmst du an, dass ein Polfilter ein Photon verändert, quasi die Polarisation „dreht“?

Nein.

Wenn das Licht den Polarisator passiert, findet eine quantenmechanische Messung statt. Das Ergebnis der Messung kann aber keinen exakten Wert (Zustandsgröße) enthalten, sondern nur eine Wahrscheinlichkeit, nämlich die, das dass Licht zum Zeitpunkt der Messung senkrecht zu seiner Ausbreitungsrichtung eine "Vorzugsrichtung" besitzt, welche sich durch den verwendeten Polarisator offenbart. Durchläuft das polarisierte Licht einen weiteren Polarisator, findet eine erneute quantenmechanische Messung statt. Die vorherige "Vorzugrichtung" geht dabei verloren.

Wäre dem nicht so, könnte polarisiertes Licht keinen zweiten Polarisator durchlaufen.

@skagerak

skagerak schrieb:Da komme ich jetzt wieder nicht ganz mit.
Ich dachte ein Überlagerungszustand ist eben ein Überlagerungszustand, und nicht "irgendeiner“ von vielen Überlagerungszuständen? 🤔

Hat sich die Frage mit dem letzten Bild in meinem Post geklärt?

@mojorisin


Schöner Beitrag bzw. Erklärung :Y:

Nur folgendes ist mir nicht ganz klar
und zwar das Bild mit den blauen Zustandsvektoren:

mojorisin schrieb:In der klassischen Physik können wir anhand des Zustandes das gesamte betrachtet physikalische System beschreiben. Fangen wir mit etwas ganz einfachem an, einem massebehaftets punktförmiges Modellobjekt das sich nur entlang einer Achse bewegen kann. In der klassischen Physik ist der gesamt Zustand beschrieben mit der Orts- und der Impulsinformation. Der Zustandsvektor gibt uns jetzt zu jedem Zeitpunkt an wo sich das Objekt befindet und mit welcher Geschwindigkeit.

Wieso gehen die immer vom Koordinaten-Ursprung aus
(und werden dabei immer länger)?

mojorisin schrieb:Hat sich die Frage mit dem letzten Bild in meinem Post geklärt?

Ja, ich denke schon. Vielen Dank.
Hab mich auch noch mal nebenbei etwas be-videoniert., also für Laien ;-)

mojorisin schrieb:Hat sich die Frage mit dem letzten Bild in meinem Post geklärt?

Danke ja, ich denke schon. Werde mich bei Zeiten wieder damit beschäftigen.

delta.m schrieb:Wieso gehen die immer vom Koordinaten-Ursprung aus
(und werden dabei immer länger)?

Die blauen Pfeile sind drei zufällig ausgewählte Zustandsvektoren des Systems. Das die Pfeile immer vom Koordinatensystemursprung ausgehen, ist so weil die Vektoren auf den Koordinatensprung bezogen werden. (siehe Ortsvektor).

Die drei Pfeile sind beispielhaft für den Zustand des Systems zu drei verschiedenen Zeitpunkten. Im Diagramm ist jetzt keine Skale aber beoispielsweise könnte der Zustand zum Zeitpunkt t1 folgender sein: Das System hat ein Impuls von p = 5~kg\frac{m}{s} und befindet sich am Ort p = 1~m.

Das ganze kann man jetzt als Vektor schreiben mit dem Zustandsvektor \vec{z}. Dann wäre der Zustand des Systems zur Zeit t = t₁



Wei dsa Beipiel an einem Teilchen ohne äußere Kräfte gemacht wurde, ändert sich der Impuls nicht aber, da das Teiclhen sich bewegt ändert isch der Ort mit der Zeit und somit auch der Zustand. Zum Zeitpunkt t = t₂ befindet sich dsa Teilchen dann z.B. bei x = 5 m. Der Zustand bei t = t₂ wäre dann:

.

Eng mit dem Konzept des Zustandes verknüpft ist der Phasenraum. Das ist ein abstrakter Raum in dem die Menge aller möglichen Zustände eines Systems dargestellt werden können. Eine anschauliche Erklärung findet man hier: https://physik.cosmos-indirekt.de/Physik-Schule/Phasenraum

Für das Verständnis der QM ist das grundlegende Verständnis was Zustände sind und was der Phasenraum ist ausgehende von der klassischen Mechanik unheimlich wichtig. Denn die Wellenfunktion die in der QM beschreiben die Zustände eines quantenmechanischen Systems. Wie man sich aber unter einem Zustand eines physikalischen Systems vorzustellen hat kann man bereits anhand der klassichen Physik anschaulich klarmachen.

@mojorisin

Hatte diese "Ortsvektoren" fälschlicherweise mit "normalen" Vektoren verglichen
und da, wie du schreibst

mojorisin schrieb:Der Impuls eines Teilchens bleibt ohne Krafteinwirkung immer gleich

hatte ich mich gewundert, dass der Vektor immer länger wird und nicht konstant gleich bleibt.

Aber das ist ja nun geklärt - Danke dafür :)