Kleines Rechenprogramm zum Lichtsegler

aja und die Force in der Matrix ist Platzhalter, da gehört die ganze Wurst die die Force ausmacht (siehe Plots oben) reingeschrieben, nicht nur ein numerische Wert. Die Integrationsvariable läuft dann über die Fläche A, 1m^2 wird dann je nach Winkel für weniger gerechnet - bei 45° zB 1/sqrt(2) m^2.

Ok die Formel ist noch viel komplizierter wollt ihr sie wirklich wissen
Ihr könnt es euch vermutlich schon vorstellen. Die schreibt voraussichtlich Gigabyteweise RAM voll wenn man Enter drückt

@yukterez
Wünsche einen guten Morgen.. hallo.

yukterez schrieb:Nein, auch mit exakt 100kg und (200x200)m² kann ich zwar über die Exzentrizität der Erde eine längere Fallstrecke rausholen und damit so ziemlich genau auf 441km/sek (440.37km/sek) kommen, aber am Ende verliere ich nach dem Swing By recht schnell fast 120km/sek und pendle mich dann bei 322km/sek ein.

Nun habe ich mir das nochmal angesehen, zw. 2-3 Sr beschleunigt die ob. genan. Masse auf 501 Km/s.
während sie folgend bis 360 Sr auf 441 Km/s abbaut. Vlt. liegt es ja daran, was bereits in ersten Rechnungen von mir vermutet, der Strahldruck bei 2-3 Sr "könnte" stärker sein als... Was geht in Ihrer letzten Rng. ein bei 2-3 Sr?
MfG

Z: Nun habe ich mir das nochmal angesehen, zw. 2-3 Sr beschleunigt die ob. genan. Masse auf 501 Km/s. während sie folgend bis 360 Sr auf 441 Km/s abbaut. Vlt. liegt es ja daran, was bereits in ersten Rechnungen von mir vermutet, der Strahldruck bei 2-3 Sr "könnte" stärker sein als...

Dazu müssten wir nicht nur die Animation, sondern auch die Herleitung derselben sehen. Ohne die Rechnung dahinter ist es leider nur eine Hausnummer...

Z: Was geht in Ihrer letzten Rng. ein bei 2-3 Sr?

Ich verstehe die Frage nicht, alles was in meine Rechnung eingeht ist ja eh am Screenshot zu sehen !

Aber der Strahldruck kann es in dem Fall nicht sein, die Differenzgeschwindigkeit wird ja in dem Fall schon beim Anflug an die Sonne angesammelt. Die Formel für den Gravity Assist ist aber garantiert richtig, da die als einzige nicht auf meinem Mist gewachsen ist, sondern tatsächlich so gelehrt wird...

@yukterez
Guten Abend... wollte keinesfalls die Kompetenz der Rng. anzweifeln. Das entsprechende Satzgebäude, kommt zudem aus temporärem Mangel an Zeit zustande. Natürlich kann man angefragtes, anhand Ihres ausgezeichneten Beispiels selbst entnehmen. Hatte heute ganze 15-20 Min. und werde in der Nacht die Berechnung nachholen, die zum angefragten führt. Es ging mir um anliegenden Strahldruck bei 2-3Sr.
Ich hatte hierzu geschrieben, bevor Sie sich freundlicher Weise des Themas annahmen..:

Zu berechnende Strahlungleistung der Sonne im Abstand von 3 Sonnenradien: (Zuerst die Kleinigkeiten) Da das 1/r² - Abstandsgesetz der Bestrahlungsstärke nur dann korrekte Werte liefern kann, wenn der Abstand zum Emittenten die tatsächliche Ausdehnung des Emittenten entsprechend übersteigt, werde ich die Strahlleistung mit folgender Begründung mitteln.
Da der Sonnendurchmesser 2 Sr (Sonnenradien) beträgt, und die Entfernung zum Startzeitpunkt 0, nur 3 Sr, sollte man 2 Werte eingehen lassen. Die Strahlleistung im Abstand von 2 Sr und die im Abstand von 3 Sr (anhand Proportionalität der Flächen mit 4*pi*r² berechnet)

Ich will Fakten hören von euch Ufogläubigen! (Seite 106) (Beitrag von Z.)
Beitrag vom 26.12.2012

Vielen Dank für Ihr Verständnis.
MfG Z.

Werter Herr Z,

Sie können um Zeit zu sparen auch meine Vorlage
http://yukterez.ist.org/Solarsail_Yukterez.nb
verwenden, dort habe ich alle Daten die man varrieren kann
(Dichte, Nutzlast, Start- und Endposition)
orange hinterlegt, dann brauchen Sie nur noch Ihre Werte einsetzen,
"Evaluate Notebook" im Menü "Evaluation" wählen und Ihre Geschwindigkeiten abzulesen.
Das dürfte Ihnen bis zu einer halben Stunde Formeleingabe ersparen.

mvH, Yukterez

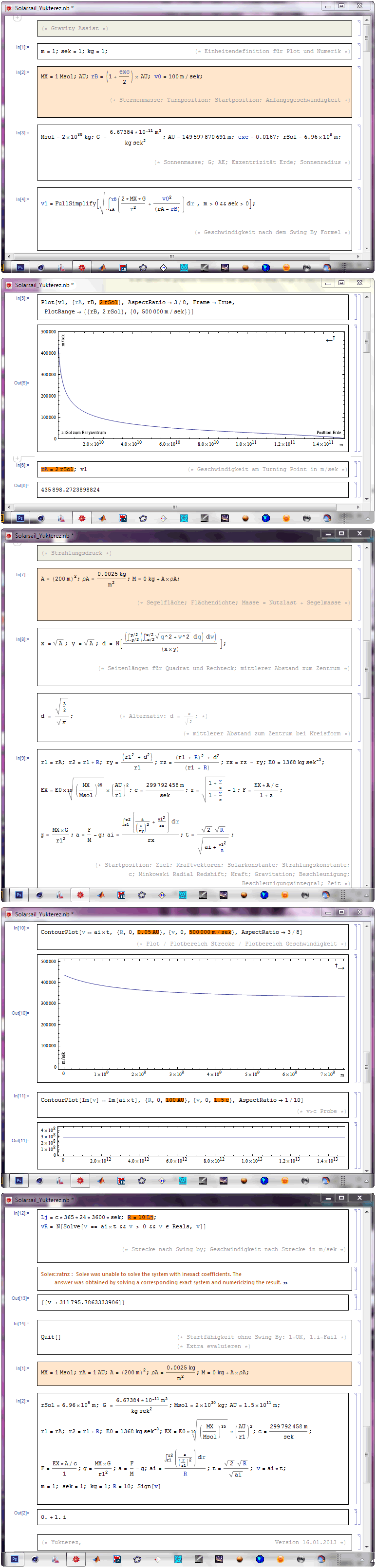
Da noch 3 Schlampigkeitsfehler in der Syntax waren werde ich den Admin bitten den alten zu entfernen. Hier die Korrektur, damit ihr euch nicht selbst durch den Salat wühlen müsst:

@nocheinPoet

Das ist wahrscheinlich die Syntax wenn man nach den verschiedenen Abständen und Winkeln bei einem sehr großen Segel integrieren möchte. Hier Segelquadrat mit 10^9m Seitenlänge, in 25 Teile per Matrix aufgeteilt und auf den Mittelwert integriert. Ich kanns heute nicht proberechnen weil mein Laptop auf 19 Volt läuft und 20 Volt braucht, ich hoffe ich finde morgen ein richtiges Kabel. Bis dahin könnt ihr schaun ob sich eh kein Fehler eingeschlichen hat, auf dem Papier sieht es für mich so aus als müsste es stimmen.

// Mupad Syntax für Segelquadrat 1e9*1e9 m^2 DIGITS := 16: kg := 1: m := 1: sek := 1: Sail := 1e9/5* // Variable matrix(5, 5, [sqrt(8), sqrt(5), (2), sqrt(5), sqrt(8), sqrt(5), sqrt(2), (1), sqrt(2), sqrt(5), (2), (1), (0), (1), (2), sqrt(5), sqrt(2), (1), sqrt(2), sqrt(5), sqrt(8), sqrt(5), (2), sqrt(5), sqrt(8)]): Msol := 2e30*kg: MX := ----*Msol: // Variable rSol := 6.96e8*m: AU := 149597870691*m: exc := 0.0167: rA := ----*rSol: // Variable rB := ----*(1+exc/2)*AU: // Variable v0 := 100*m/sek: // Variable G := 6.67384e-11*m^3/kg/sek^2: v1 := sqrt(int(2*MX*G/r^2+v0^2/(rA-rB), r=rA..rB)); A := 1e9^2*m^2: // Fläche pA := 0.0025*kg: // Dichte M := 100*kg+A*pA: // Masse mit Nutzlast r1 := rA: E0 := 1368*kg/sek^3: EX := E0*(MX/Msol)^3.5*(AU/r1)^2: c := 299792458*m/sek: z := sqrt((1+v/c)/(1-v/c))-1: F := EX*A/c/(1+z): g := MX*G/r1^2: a := F/M-g: r1 := rA: rx := (r2-(r1^2+Sail^2)/r1): // Delta Matrix ry := sqrt(r1^2+Sail^2): // Anfangsdistanz Matrix rz := ((r1+R)^2+Sail^2)/(r1+R): // Enddistanz Matrix ai := int(a/(r/ry)^2+v1^2/rx, r=ry..rz)/rx: t := sqrt(2)*sqrt(rx)/sqrt(ai+v1^2/rx): R := ----*AU: // Entfernung V := mean(mean(solve(-v+ai*t, v)))

Findet noch wer einen Fehler in meiner Herleitung ?

(Man könnte natürlich noch den Stern integrieren nach seinen verschiedenen Abständen, Zentrum und Rand, etc, aber ich weiss nicht ob wir's so genau brauchen :)

Ich sehe gerade bei mupad geht der mean command nicht, das heisst hier offenbar anders. Damit die matrix elementwise gerechnet wird muss man es auch noch anders hinschreiben, ich habe hier die matlab syntax verwendet um einen mupad code zu schreiben. Aber ich denke es sollte soweit klar sein wie es gerechnet gehört. Auch bei ry hat sich ein kleiner fehler eingeschlichen, der hiermit korrigiert wird auf:

ry := (r1^2+Sail^2)/r1: // Anfangsdistanz Matrix

(weil es nicht nur die Distanz, sondern auch der Kraftvektorbetrag ist). Ich wälz mich mal durchs Tutorium um eine passende Input Form zu finden.

Segel > Sonnendurchmesser, Teil 2

Ich hab das mit der Mupad Matrize noch nicht heraussen wegen der elementweisen Potenz (aber einen Thread offen im gomatlab Forum), in Matlab kann ich mittlerweile numerisch ein Ergebnis solven. Zur Probe nehme ich wieder eine Konfiguration die nahe an c führt, damit wir auch sehen, daß es alles brav unter c bleibt. Hier also die Rechnung von oben inputfähig in Matlab Syntax mit Ergebnis:

% Matlab Syntax (Yukterez v.01/2013) syms r v kg m sek positive kg = 1; m = 1; sek = 1; Sail = 1e9/5*m*([sqrt(8),sqrt(5),(2),sqrt(5),sqrt(8);sqrt(5),sqrt(2),(1),sqrt(2),sqrt(5);(2),(1),(0), (1),(2);sqrt(5),sqrt(2),(1), sqrt(2),sqrt(5);sqrt(8),sqrt(5),(2),sqrt(5),sqrt(8);]); Msol = 2e30*kg; MX = 40*Msol; % Variable rSol = 6.96e8*m; AU = 149597870691*m; exc = 0.0167; rA = 10*rSol; % Variable rB = 10*(1+exc/2)*AU; % Variable v0 = 100*m/sek; % Variable G = 6.67384e-11*m^3/kg/sek^2; v1 = vpa(sqrt(int(2*MX*G/r^2+v0^2/(rA-rB), r,rA,rB))) A = 1e9^2*m^2; % Fläche pA = 0.000025*kg; % Dichte M = 10*kg+A*pA; % Masse mit Nutzlast r1 = rA; E0 = 1368*kg/sek^3; EX = E0*(MX/Msol)^3.5*(AU/r1)^2; c = 299792458*m/sek; z = sqrt((1+v/c)/(1-v/c))-1; F = EX*A/c/(1+z); g = MX*G/r1^2; a = F/M-g; R = 100*AU; % Entfernung r1 = rA; ry = mean(mean((r1^2+Sail^2)/r1)); % Anfangsdistanz Matrix rz = mean(mean(((r1+R)^2+Sail^2)/(r1+R))); % Enddistanz Matrix rx = mean(mean(rz-(r1^2+Sail^2)/r1)); % Delta Matrix ai = int(a./(r./ry)^2+v1.^2./rx, r,ry,rz)/rx; t = sqrt(2).*sqrt(rx)./sqrt(ai+v1.^2/rx); V = (solve(-v+ai*t, v)) _____________________________________ v1 = 1 235 774 % m/sek V = 283 571 434 % m/sek

Ich habe den mean Command hier eine Ebene tiefer gesetzt; das spart Rechenleistung. Ich hoffe das ist zulässig, aber nach der Proberechnung unten sollte es das sein:

a = 2.828427124746190 2.236067977499790 2.000000000000000 2.236067977499790 2.828427124746190 2.236067977499790 1.414213562373095 1.000000000000000 1.414213562373095 2.236067977499790 2.000000000000000 1.000000000000000 0 1.000000000000000 2.000000000000000 2.236067977499790 1.414213562373095 1.000000000000000 1.414213562373095 2.236067977499790 2.828427124746190 2.236067977499790 2.000000000000000 2.236067977499790 2.828427124746190 >> mean(mean(sqrt(a))) = 1.324145771252110 >> sqrt(mean(mean(a))) = 1.324145771252110 -> OK

Soweit alles klar nach Pythagoras ?

Zur Illustration meines Rechenganges:

Man kann die Formel wie es aussieht noch weiter vereinfachen (und vielleicht sogar auf die Matrix verzichten) wenn man es schafft, folgendes einzubaun: http://netmathematik.de/forum/index.php?page=Thread&postID=28216#post28216

Ich stell das Update sobald verfügbar auf http://yukterez.ist.org/segelmatrize.txt ⁽*⁾ anschnur.

____

⁽*⁾ ist.org⇄enabled.io

@yukterez
Finde es etwas schade, das dieser hochwertige Thread evtl. im irgendwo untergeht...
Kann Ihre Arbeit am Thema, nun mit dem letzten Post, als abgeschlossen gelten?
Falls ja ist keine Antwort nötig.

Ich werde mich dann die nächsten Tage nochmal mit verschiedenen Betrachtungen zur Arbeit und zum Thema melden.

Hochachtungsvoll Z.
(Ps zu von mir angefragtem liegen bereits erste Audioarbeiten an, es geht voran.)

Meines Erachtens ist es abgeschlossen. In der Zwischenzeit fand ich übrigens heraus, daß mit herkömmlichen Programmen wie Freemat höhere Geschwindigkeiten herauskommen, was einerseits an den auf 100 Intervalle beschränkten Integralen und der Beschränkung auf Computergenauigkeit (16 Gleitkommastellen) sowie der rein numerischen Vorgehensweise dieser Programme zu liegen scheint, und andererseits eine Erklärung für den höheren Wert bei der Simulation unbekannter Herkunft sein könnte. Ich halte deshalb derzeit nur die Notationen für Matlab, Mupad, Maple und Mathematica (siehe .txt file oben) für ausreichend genau, um so viele Integrale und Differentiale befriedigend zu lösen. Auf http://forum.alltopic.de/viewtopic.php?p=20032#p20032 wird nebenbei noch an einer GPL Lösung gearbeitet, aber das ist nur noch eine Frage der Notation, nicht der Formeln.

Ich habe das File

yukterez.ist.org/Solarsail_Yukterez.nb

upgedatet, man kann jetzt auch grössere Segel als Sonnendurchmesser bzw. Abstand haben.
(Es ergibt als .nb File eine schönere Formatierung als wenn man den Quelltext aus dem .txt File kopiert und einsetzt). Nimmt man statt rechteckigen oder quadratischen Segeln runde Segel, ist der mittlere Abstand des Mittelpunktes (d), wenn ich mich nicht irre, der Radius des halben Flächeninhaltes.

Ich hab sie drüben schon gepostet, damit der Thread nicht untergeht hier nochmal die letzte Version wo alles dabei ist in übersichtlicher Schreibweise.

Der Thread ist zwar schon alt, aber zum Glück ist es noch niemandem aufgefallen dass sich ein kleiner Schönheitsfehler in der Rechnung befindet. Dieser hat zwar keine groß bemerkbaren Auswirkungen auf das Ergebnis, aber ein paar Prozent Abweichung gibt es dadurch trotzdem.

Der Hund liegt im Feld In[9] in der letzten Zeile. Dort hatte ich die Beschleunigung auf die Strecke integriert, um Geschwindigkeit und Zeit nach Strecke zu erhalten. Das ist aber nicht die sauberste Lösung. Wenn man das ganze als Differentialgleichung schreibt kann man Beschleunigung, Geschwindigkeit und Position abhängig von der Zeit erhalten.

Dafür muss man die Notation ein bißchen ändern und die Geschwindigkeit als Derivative eingehen lassen. Also streicht man bei In[9] in der vorletzten Zeile alles ab "z=..." heraus und ersetzt ab dort durch

z := Sqrt[(c + P'[t])/(c - P'[t])];
F := (EX*A/c)/z;
g := (MX*G)/r1^2;
a := F/M-g;

s = NDSolve[{P''[t] == a, P'[0] == v1, P[0] == r1}, P, {t, 0, tMax}]

Plot[Evaluate[P''[t] /. s], {t, 0, tMax}] (* Beschleunigung *)
Plot[Evaluate[P'[t] /. s], {t, 0, tMax}] (* Geschwindigkeit *)
Plot[Evaluate[P[t] /. s], {t, 0, tMax}] (* Position *)

wobei tMax die zu evaluierende Flugzeit des Segels im Inertialsystem des ruhenden Beobachters ist. Neu plotten muss man nicht, da die zu erreichende Geschwindigkeit in etwa gleich ist, aber vielleicht modernisier ich den Code demnächst mal so dass man auch die Eigenzeit des beschleunigten Segels dazuerhält.

Korrigierend,

Yukterez

Moin @yukterez ,

Und hast Du modernisiert?


Gruß

neP