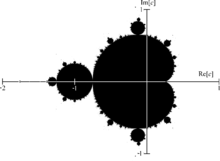
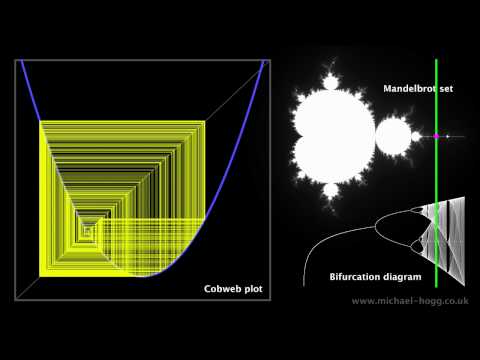
Fraktale? Mandelbrotmenge?

Hi Community,

ich war ebend bisschen in Wikipedia am stöbern über Rastergrafiken und Vektorgrafiken, bin dann zur Seite über Grafikprogramme gestoßen, wo am Ende etwas über Fraktale stand:
"Interessant für die Arbeit von Computergrafikern sind Fraktalgeneratoren zur Erzeugung von Fraktalen."
Jetzt bin ich natürlich auf die Seite zur Beschreibung von Fraktalen gegangen und da hab ich dann einfach garnichts mehr kapiert. Es wird über eine Mandelbrotmenge geredet und über eine Julia-Menge, über eine Hausdorff-Dimension usw...
Das einzige was ich hierbei noch verstehe ist mit den Iterationsstufen. Dennoch klingt das Thema irgendwie interessant. Meine Frage jetzt ob jemand das Thema vielleicht etwas einfacher erklären kann und bisschen mehr dazu sagen kann was es damit auf sich hat und wofür man sowas gebrauchen kann?

Hier der Link: Wikipedia: Fraktal

Mfg ElGreco

Also vorallem diese Zoomfahrt bei der Mandelbrotmenge hier finde ich auch verwirrend:

Wikipedia: Mandelbrot-Menge#Bildergalerie einer Zoomfahrt

Ich glaub ich bin echt zu blöd dafür :(

Hallo @elgreco1 :)

Kannst du ein bisschen Englisch? Wenn ja, dann wir dir auf dieser Seite alles detailliert erklärt, inklusive der Mathematischen Grundlagen und alles wunderschön mit Animationen versehen:

http://acko.net/blog/how-to-fold-a-julia-fractal/

Wirklich eine der genialsten Webseiten im ganzen Internet. Einfach runterscrollen, durchlesen, und die Bildergalerien durchklicken. Danach sollte alles klar sein ;)

Ansonsten ist der Sinn solcher Fraktaler sehr vielfältiger Natur. Einerseits sind ihre Eigenschaften von grundlegendem mathematischen Interesse. Andererseits werden sie gerne in der Computergrafik benutzt, um zum Beispiel prozedurale Texturen zu erzeugen, oder künstliche Landschaftsprofile. Du kannst auch zum Beispiel Raucheffekte damit generieren.

Allgemein kann man sagen, dass die Mandelbrotmenge eine spezielle Menge von komplexen Zahlen ist. Du fängst mit einer Zahl c an. Dann quadierst du sie und addierst die ursprüngliche Zahl c wieder dazu.

z = z²+c

Je nachdem mit welchem c du anfängst beginnt diese Zahlenreihe entweder in der Unendlichkeit zu verschwinden, oder sie bleibt in der Nähe des Urprungs. Alle c's, für die die dazugehörige Folge von Zahlen nicht in die Unendlichkeit abhaut sind dann Teil der Mandelbrotmenge. Und wenn man diese Menge aufzeichnet bekommt man eben dieses Bild:



Das sieht schon interessant aus und es ist auch ganz erstaunlich, dass aus der simplen Formel so eine komplizierte Form entstehen kann. Aber noch verrückter wird es, wenn du nicht die Mandelbrotmenge betrachtest, sondern alle Punkte, die eben schon in die Unendlichkeit verschwinden. Wenn man diese Starpunkte einfärbt, je nach der "Geschwindigkeit" der dazugehörigen Zahlenfolge, dann entstehen diese tollen Bilder.
Das erstaunliche ist jetzt, dass man in diese Figur beliebig tief reinzoomen kann, und trotzdem immer neue Formen sichtbar werden.

Aber wie gesagt, schau dir den Link oben an, der ist Gold wert. Und wenn das nicht reicht hab ich noch viel mehr für dich ;)
Und wenn du Fragen hast, einfach stellen.

Ok danke für die Hilfe @HYPATIA Die seite sieht echt interessant aus und schön gestaltent werd sie mir auf jeden fall angucken :)

http://www.fractalizer.de/
noch eine interessante Seite, sogar auf deutsch ^^

kann mir jemand den (mathematischen) Unterschied der Mandelbrotmenge zur Juliamenge erklären?

@blackbird.
Das ist relativ einfach :)

Grundsätzlich geht es immer um die Folge



Die Parameter a und c sind komplex, deswegen hängt die Folge von vier reellen Parametern an. Es ergibt sich daher eine vierdimensionale Figur, wenn man sich anschaut, für welche Parameter sich eine nichtdivergierende Folge ergibt.

Nun sind 4D-Figuren etwas blöd zu zeichnen, deswegen rendert man in der Regel nur zwei Dimensionen, während man die anderen beiden festhält. Dabei gibt es 6 verschiedene Möglichkeiten, Schnitte durch die 4D-Julia-Menge zu machen.

Ich kann z.B. c auf 0+0i setzen, dann ergibt sich logischerweise ein Kreis beim Rendern über verschiedene a:



Wenn ich stattdessen a auf 0+0i setze und über c rendere ergibt sich das bekannte Mandelbrot-Bild:



Die anderen Möglichkeiten ergeben sich aus dem jeweiligen Nullsetzen von zwei Werten (Real- bzw. Imaginärteil) und dem Rendern über die anderen beiden:




So, die "klassischen" Juliamengen bekommst du jetzt, indem du c auf einen beliebigen Wert setzt (für Null hab ich ihn ja schon oben geposted) und dann über a renderst.


Das ist also genau das Gegenteil wie beim Mandelbrot. Dort wird der Startwer a auf Null gesetzt und dann die verschiedenen Verschiebungen c betrachtet.



Was du jetzt machen kannst, ist ganz viele verschiedene Juliamengen rendern, und dann anhand des verschiedenen Verschiebungen c anordnen. Quasi eine Karte von Juliamengen:



Und da erkennst du dann schon ein interessantes Muster. Es scheint sich nämlich wieder das klassische Mandelbrot abzubilden. Tatsächlich bestehen ganz interessante mathematische Zusammenhänge zwischen dem Mandelbrot und den "klassischen, zweidimensionalen Juliamengen".
Jedenfalls, wenn du diese Julia-Karte detaillierter renderst erhälst du folgendes Bild:



Und das ist jetzt quasi die vierdimensionale Juliamenge herunterprojiziert auf ein zweidimensionales Bild. Du siehst natürlich stark hervorstechend das Mandelbrot, aber es ist auch erkennbar, dass "darüber" und "darunter" (und noch in Richtung der vierten Dimension) weitere Strukturen sind, die man normalerweise nicht sehen kann.

Alternativ kannst du natürlich auch ein 3D-Bild rendern, während du einen einzelnen Parameter festhältst:

Original anzeigen (0,5 MB)

-------

Edit: Julia-Mengen sind natürlich eine bestimmte mathematische Menge, die man aus viele Funktionen bilden kann. Hier gehts jetzt grade wirklich nur um die 4D-Juliamenge, die nach der obigen Folge definiert ist.

@HYPATIA
@blackbird.

Find ich schon höchst interessant. Hab da mal ein Video gefunden was ich mal vor ~3 Jahren gemacht habe.

Schon faszinierend.

https://www.youtube.com/watch?v=CFvTks2RD7c

Archerv schrieb:Schon faszinierend.

Jupp. Vor allem, wenn man sich damit ernsthaft und etwas intensiver auseinandersetzt. Julia-Mengen sind bspw. eng verknüpft mit der Chaostheorie. Und bei der Mandelbrot-Menge zu den Julia-Mengen der quadratischen Familie f_c(z)=z^2+c findet man ebenfalls so einige spektakuläre Zusammenhänge, etwa zur logistischen Gleichung oder zum Feigenbaum-Diagramm. Ganz gut übrigens von Michael Hogg im folgenden Video erklärt:

Mandelbrot set - from order to chaos

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Mir hat es damals jedenfalls mal sehr beim Verständnis der Zusammenhänge zur Chaostheorie geholfen - neben einem Haufen von Literatur und anderen Quellen, versteht sich. :)

Auch das hier ist recht hilfreich, wenn man ein wenig den Zusammenhang zwischen Mandelbrot- und Julia-Menge(n) verstehen will:

Mandelbrot Set: how it is generated

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Hypatia hatte es ja schon angedeutet: Die Mandelbrot-Menge ist im Prinzip eine Art "Landkarte" für Julia-Mengen, und zwar für ganz bestimmte Julia-Mengen, nämlich zusammenhängende Julia-Mengen. Warum die zusammenhängenden Julia-Mengen jetzt so interessant sind, hab' ich grad aber nicht mehr im Kopf. Wahrscheinlich, weil Mathematiker halt so sind und immer alles irgendwie klassifizieren wollen. :)

Sehr, sehr geil fand ich damals das Video von TeamFresh. Die "Kamerafahrt" gut gewählt und der Track passt auch sehr gut. Muss man aber wirklich auf sich wirken lassen (Vollbild+Kopfhörer+immer auf die Mitte starren :) ). Und vielleicht muss man auch ein bisschen Fan davon sein, um es zu mögen. :D

Fractal Zoom (Last Lights On) Mandelbrot (720p 30fps) e228 (2^760)

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Michael Hogg (s.o.) hatte auch mal eins gemacht, das ebenfalls nicht schlecht ist:

2010: A Mandelbrot Odyssey (FractalNet HD)

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Man findet aber natürlich auch noch einen Haufen anderer Videos. Und der Zoom-Rekord von TeamFresh (e228/2^760) wurde mittlerweile natürlich auch längst geknackt.

Und für alle, die sich die Mandelbrot-Menge selbst mal ein bisschen angucken wollen...
http://www.ultrafractal.com/

@HYPATIA
Vielen Dank!! Die Bilder sind klasse! Ich geb zu, ich hab nicht jedes Detail verstanden, aber jetzt ist die Materie mir nicht mehr so rätzelhaft. Ich bin immer wieder begeistert für das Thema. mit den 4 Dimensionen ergibt das jetzt einen Sinn :)

Also kommt es nur mir so vor oder ist die Ausgangsfunktion nicht das bestimmte Integral von f(x)=x ?
Hat das damit was zu tun oder ist das Zulall?

Und ich hab in meiner Urquelle (worüber ich auf das Thema gekommen bin: ein Höhrbuch :) ) gehört, dass die Mandelbrotmege so etwas wie die Summe aller linearen Zahlen ist. Googel will mir nicht helfen: innerhalb der linearen Algebra kann man doch auch Reelle Zahlen beschreiben.
Sind die auch in der Mandelbrotmenge? Muss n eine Natürliche Zahl sein?

@Noumenon
& @Archerv
Danke für das Material!

@blackbird.
Zieh' dir am besten den 3-Teiler hier rein...

Complex Plane Dynamics

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

How Julia set images are generated

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Mandelbrot Set: how it is generated

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

blackbird. schrieb:Also kommt es nur mir so vor oder ist die Ausgangsfunktion nicht das bestimmte Integral von f(x)=x ?
Hat das damit was zu tun oder ist das Zulall?

Und ich hab in meiner Urquelle (worüber ich auf das Thema gekommen bin: ein Höhrbuch :) ) gehört, dass die Mandelbrotmege so etwas wie die Summe aller linearen Zahlen ist. Googel will mir nicht helfen: innerhalb der linearen Algebra kann man doch auch Reelle Zahlen beschreiben.
Sind die auch in der Mandelbrotmenge? Muss n eine Natürliche Zahl sein?

Damit liegst du auf jeden Fall... äh... ganz, ganz falsch. :D

@Noumenon

Okidoki, dan schau ich mir die sache mal an. Und dann kann ich den mist da oben ja löschen. ^^

@blackbird.
Na, mit Löschen wird wohl nix. Das Löschen/Ändern eines Beitrages geht hier nur ca. 5min lang. :D

@blackbird.

blackbird. schrieb:Und ich hab in meiner Urquelle (worüber ich auf das Thema gekommen bin: ein Höhrbuch :) ) gehört, dass die Mandelbrotmege so etwas wie die Summe aller linearen Zahlen ist. Googel will mir nicht helfen: innerhalb der linearen Algebra kann man doch auch Reelle Zahlen beschreiben.
Sind die auch in der Mandelbrotmenge? Muss n eine Natürliche Zahl sein?

Ich kenne schon so einige Zahlen- Räume in der Mathematik, Lineare zahlen sind mir allerdings noch nicht unter gekommen.
Die lineare Algebra befasst sich mit Endomorphismen zwischen Vektorräumen. Reelle Zahlen sind eher das Gebiet der Analysis.

@Noumenon
oh, hast Recht :/

Schön anzusehen sind Fraktale allemal, aber wenn man richtig erfassen will, was eigentlich Sache ist, sollte man sich schon tiefgründig mit der Funktionentheorie auseinander setzen. Nicht mein Ding.

mathematiker schrieb:Die lineare Algebra befasst sich mit Endomorphismen zwischen Vektorräumen. Reelle Zahlen sind eher das Gebiet der Analysis.

Naja, da der Begriff des Endomorphismus eigentlich sehr viel weitreichender ist, sollte man wohl doch wie in wikipedia einschränkend lineare Abbildungen sagen.

@mathematiker

mathematiker schrieb:Schön anzusehen sind Fraktale allemal, aber wenn man richtig erfassen will, was eigentlich Sache ist, sollte man sich schon tiefgründig mit der Funktionentheorie auseinander setzen.

Nö, nicht unbedingt. Funktionentheorie braucht man für das Verständnis der Julia-Mengen, aber nicht für die fraktale Geometrie. Hier findet man eine ziemlich klasse Einführung in die Thematik, welches auch etwas Verständnis in Funktionentheorie voraussetzt:
http://www.ijon.de/mathe/julia/index.html (Archiv-Version vom 27.01.2013)

Für die fraktale Geometrie hingegen sind an dieser Stelle als Voraussetzungen bspw. Analysis II & Lin. Algebra II angegeben:
https://campus.tum.de/tumonline/wbStpModHB.detailPage?pKnotenNr=827964

Etwas Kenntnisse in Topologie wären sicherlich ebenfalls nicht schlecht, sind aber nicht zwingend erforderlich.

Das Niveau der HP dort oben ist noch vergleichsweise niedrig. Die höhere Theorie der Julia-Mengen hat's aber schon derbe in sich. Hatte da mal reingeschnuppert... diverse Literatur, Skripte... die Arbeiten von Douady/Hubbard findet man afaik auch irgendwo im Netz. Das ist schon recht böses Zeugs und war mir dann doch zu viel... :D

mathematiker schrieb:Naja, da der Begriff des Endomorphismus eigentlich sehr viel weitreichender ist, sollte man wohl doch wie in wikipedia einschränkend lineare Abbildungen sagen.

Nö, naja, jede lineare Abbildung f ist ja ein Homomorphismus, und zwar von Vektorräumen, etwa f:V->W. Und bei einem Endomorphismus gilt einfach V=W. Aber die Theorie dahinter ist natürlich ziemlich weitreichend, ja.