Kann Licht schwarzen Löchern entkommen?

Hoffentlich ist deine Einstellung der Natur gegenüber als Physiker eine andere.

Im Weltbild des Unterzeichnenden ist der Beschuldigte dämonisch besetzt und schreibt vermutlich aus der Psychiatrie der Universität Wien, wo er auch hingehört.

Okay, von solchen Erfahrungen sprach ich natürlich nicht :D.

Aber wenn es da schwarz auf weiß steht, dann muss doch was dran sein...

schnell wegduckend

Peter

Uuups, und schon ist Y wieder verschwunden. Jetzt machen die beiden oberen Kommentare auch keinen Sinn mehr :D

Mal sehn, wie schnell der nächste Account gebastelt ist...

@Peter0167
Also der Wärter hat gesagt, ich dürfte noch ein bisschen ins Netz, deshalb nutz ich die Zeit doch einfach mal schamlos aus, hier in der Insel, unweit von Y. ;)
Hinter den Horizont Linien gehts weiter
-------------------------------------------------------------------------
Deswegen erstmal wegen dem Kontext bzgl Reihenfolge zu:
@nocheinPoet

@Z.
Der EH strebt dem Objekt nun entgegen und verschluckt diese bevor Zeitdilatationszone Max erreicht.

Poet schrieb:

nocheinPoet schrieb:Das ist keine Tatsache, sondern Deine Meinung und eben der strittige Punkt mit Y. Oder?
Eben. ;)

Nun das ist kompliziert :)
Ich verwende eine etwas andere Darstellung, als Toms und Dr. Stupid, in meiner Grafik.

Während Toms und Dr Stupid, allgemein auf die.... gesamte Ausdehnung... der Sphäre des EH M abstellen, der sich um den geometrischen Faktor rs m vergrösseren wird.... und dann die Zeit t von rs m berechnen bis rs m im Abstand seines eigenen Radius rs=m auf den sich ausdehnenden EH Rs M + rs m gefallen ist....

...lasse ich den EH nur am Ort des Geschehens auf rs m zustreben und begründe dies mit der ART und zwar EIT.
m würde exakt auf dem EH eine unendliche Energie bekommen, bevor das aber passiert.....


...flukturiert EH M ....

... am Ort des Geschehens zu rs m.

Es bleibt sich insofern gleich was passieren wird. rs m wird noch vor erreichen von exakt ..

vom expandierenden EH M verschluckt.

Deutlicher ist das aber in meiner punktuellen Darstellung zu entnehmen, da die gesamte Ausdehnung/Expansion von EH M a. kaum grafisch darstellbar. b. Ausserdem erklärt mein Ansatz imho schlüssig anhand ART-Faktoren warum EH M am Ort des Geschehens tatsächlich zu rs m flukturiert/expandieren wird. Eben genau deswegen weil der Impuls p von m so nahe EH M zu unendlich tendiert.
Damit stiege die Energie von m ins unendliche* somit auch dessen Energie-Masse-Äquivalenz.
Eben exakt auf....

...wäre das theoretisch der Fall.

Zusatz zum Problem: ;)
Dies ist meiner Meinung aber zu vermeiden* und kann vermieden werden wenn man die ART voll eingehen lässt.
Eben genau dann wird EH M zunächst nicht Global sondern nur punktuell flukturieren und rs m noch bevor es zur unendlichen Energie auf Rs M kommt, von EH M´, M´=Asymptote am EH, verschluckt.
m geht somit mit endlicher Energie in den EH ein. ;)
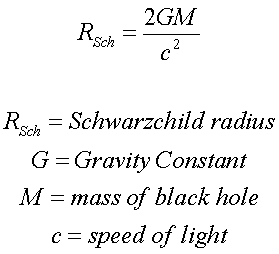
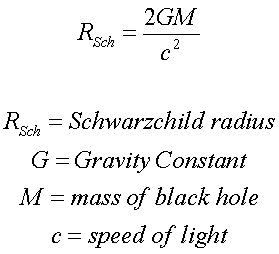
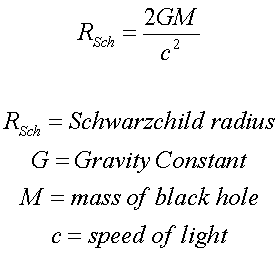
Darüber und über die Hintergründe können wir uns gerne unterhalten. Du hast ja ein gutes Back Up sozusagen ;)
-------------------------------------------------------------------------------------------------------------------------------------

Peter

Peter0167 schrieb:Daher schnell zu meiner Frage oder meinem Problem: Ist es sinnvoll, für die Beschreibung solcher Vorgänge (Sturz eines Objektes in ein SL) nur die Position eines äußeren Beobachters einzunehemen? Offensichtlich sorgen relativistische Effekte dafür, dass die Ergebnisse nicht standortunabhängig sind.

Aus Sicht des äusseren Beobachters bleibt es eben physikalischer. (Innen können wir nicht messen nur vermuten)
Natürlich nur wenn wir auf einen Beobachter nahe EH M abstellen, der zb seine eigene bekannte Masse m Beschleunigen muss=Impuls um seine Position zu halten, somit die Auswirkungen von M und desweiteren tatsächliche Messungen an dortigen asyptotischen Metriken und Gegebenheiten wie seinen Impuls vornehmen/ableiten kann.
Ein Beobachter im unendlichen der in einer flachen M-Metrik weilt und zudem keine Messungen vornehmen kann ist ungeeignet. Dessen Näherungen sind ungenau.

Peter0167 schrieb:Wenn ich z.B. ein Schiff beobachte, welche auf dem Weg nach Amerika ist, dann würde ein Beobachter, der am Strand zurückbleibt, niemals sehen, wie das Schiff dort ankommt, im Gegenteil, aus dieser Position sähe es so aus, als ob das Schiff am Horizont versinkt. Ein Passagier an Board würde eine vollkommen andere Beobachtung machen, für ihn versinkt das Schiff nicht, und er würde irgendwann die Ankunft in Amerika miterleben.

:D Y. hätte imho wahrscheinlich nun mit der Titanic Argumentiert ;)
Die Erklärung hast du ja oben.... warum sich ein naher und ein unendlicher Beobachter qualitativ unterscheiden.
Die Idee die Messungen auf dem Weg ins Loch vorzunehmen ist gut, nur lässt sich das leider nicht mehr wiederholen :D
Aber du hast recht... man sollte somit auf alle möglichen Überlegungen/Blickwinkel zurückgreifen.
Nicht umsonst hat sich Albert selbst auf einem Lichtstrahl reitend vorzustellen versucht.
LG Z.

Es gibt zu diesem Problem der "Event Horizon deformation" eine Ausarbeitung eines Bachelor-Studenten! Hiermit sollten eigentlich alle Fragen geklärt werden:

Die Original-veröffentlichung:
http://journals.aps.org/prd/abstract/10.1103/PhysRevD.84.124015

Das ganze auf ArXiv:
http://arxiv.org/pdf/1007.5387v2.pdf

Die Original-Bachelorarbeoit:
http://web.stanford.edu/~rhamerly/cgi-bin/Academics/ResearchThesis.pdf (Archiv-Version vom 14.07.2015)

Aber ich habe meine Zweifel das das hier anwesende, inklusive mir (da bin ich mir sicher) einfach mal so evaluieren können.

Viel Spaß damit ;-)

@mojorisin

We further show that among the leading-order horizon area increase, half arises from generators that enter the horizon through the caustic, and the rest arises from area increase near the caustic, induced by the gravitational field of the compact object.

Volltreffer...versenkt!
Danke ;)
LG


PS @all
"caustic"
Bitte bei Optik nachschauen.

Z. schrieb:Aus Sicht des äusseren Beobachters bleibt es eben physikalischer.

Naja, bis zum EH bleibt es auch aus Sicht des einfallenden Objektes "physikalisch" :D

Nun hatte ich gerade ein Video gefunden, von dem ich mir des Titels wegen mehr erhofft hatte, aber auch da wird zuerst auf einen äußeren Beobachter zurück gegriffen. Die Bilder sind aber trotzdem interressant :D

https://www.youtube.com/watch?v=TR6VArXZBuA (Video: Reise IN ein Schwarzes Loch)

@all


Ich lasse das innere Photon hier in meiner Grafik (vergrö. Teilausschnitt) nach aussen propagieren.
Photon=Gelbe Spitze aufs Objekt Schwarz rs m zulaufend.
Analog die Form des einfallenden Objektes.
Der EH wir dort imho asymptotisch über Rs M hinaus flukturieren=Graue Linie.

Vergleich Paper:

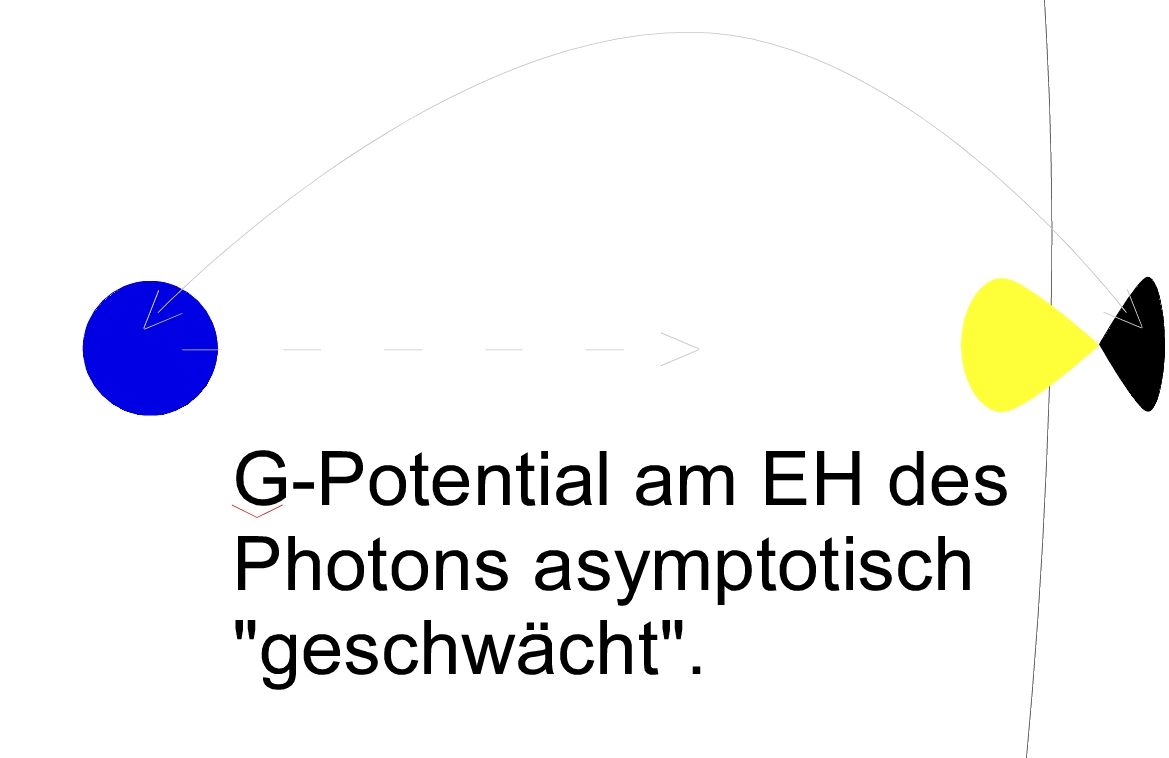
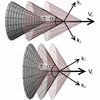
FIG. 6: Viewed as a 2-surface in 3-space, the horizon near
the caustic looks like a cone of angle π − α. This is shown
for a small cone angle (top) and a larger cone angle (bottom),
both cones propagating to the right as time progresses (three
time slices of the horizon are shown in the figures). Like a
Cherenkov cone, the speed Vc > c increases as the cone angle
decreases.

@Peter0167
Hier Peter eine Sicht eben nicht mal vom einfallenden Objekt ..sondern vom EH gesehen ;)
Rumsitzen kann förderlich sein, besonders hier in der Anstalt. :D
NG

Peter0167 schrieb:Wenn man ein Schwarzes Loch auf seine zentrale Singularität beschränkt, kommt das evtl. hin, wobei Singularitäten keine Erfindung der Mathematik sind. Auch physikalisch gesehen hat ein SL der Theorie nach eine zentrale Singularität.

Mathematisch handelt es sich um einen Punkt, so wie ich das verstanden habe. Da Z aber irgendwelche Kerr Lösungen ins spiel bringt ist es halt nun nicht mehr nur ein Punkt. Zudem Rotiert dieser auch noch um seine eigene Achse.

Peter0167 schrieb:Naja, bis zum EH bleibt es auch aus Sicht des einfallenden Objektes "physikalisch" :D

Anderes beispiel. Messung/Beobachtung beisst sich mit der Quantenphysik und trotzdem wird an ihr festgehalten.

@Z.

Interessant dürfte eine noch ausstehende Publikation von Hamerly werden. Zu der von @mojorisin zitierten, die nur für ein statisches Schwarzes Loch gilt, ist eine Arbeit zu einer Kerr-Lösung erarbeitet worden. Zum oben zitierten Paper schreibt der Autor:

These results only apply to mergers of Schwarzschild black holes, however. Since real astrophysical black holes have spin, we are currently working on extending our results to the Kerr case. This is not as easy as it sounds. There is no widespread metric perturbation formalism for Kerr black holes, and even if such a formalism did exist, it would be very, very nasty. Qualitatively different methods must be used if we are to tackle the Kerr case.

One such method takes note of the fact that the event horizon is only substantially affected near the small black hole's trajectory. If we take a local frame enclosing the small black hole (like a Fermi normal frame), the metric becomes nearly flat, and the large black hole becomes akin to a Rindler spacetime. We have been able to extend our results to the Kerr case using this method (at least for the part of the horizon near the small black hole's infall), but the work is not yet ready for publication.

Another plausible but less developed possibility is to abandon our coordinate-dependent approach and look only at coordinate-independent quantities — i.e. the expansion r and the shear s. To find r and s, one must first find y_0 using the Teukolsky Equation. Hopefully, this method too will bear fruit in the future, but only time will tell.

http://web.stanford.edu/~rhamerly/cgi-bin/academics.php

ornis schrieb:Zu der von @mojorisin zitierten, die nur für ein statisches Schwarzes Loch gilt

Was auf die wenigsten SL auch zutrifft. Die meisten von denen Rotieren.

@ornis
Danke für deine Bemühung.
Es ist klar das eine Ableitung bzgl der Lösung der Einstein Gleichung = Schwarzschild Lösung, nicht rotierend.
auch übertragbar ist auf die zweite Lösung = Kerr-Lösung, rotierend
Imho muss es das auch, da siehe beides Lösungen des Einsteinschen Gleichungssystems.

Besonders bemerkenswert betr. des Autors zur Kerr-Lösung ist folgender Satz! (Deines Links)

General relativity is not something that you learn once. Rather, much like field theory, it is something that must be re-learned over and over again. Thus, when I took Caltech's gravitation course (Ph 236ab), I learned many more subtleties that had not stood out in Landau-Lifshitz.

"Ja Albert tolles Drehbuch!"

NG

@fritzchen1

fritzchen1 schrieb:Was auf die wenigsten SL auch zutrifft. Die meisten von denen Rotieren.

Lies mal oben drüber du.... Fritzschen du...... liebstes :)
NG

@ Z.

Was ich an Deinem Beitrag nicht nachvollziehen kann, aber da hilfst Du mir sicher gerne, ist die folgende Aussage:
"Was das Tunneln betrifft, laut ART hätten wir an der EH Sphäre nach draussen eine unendlich Große Potentialbarriere* zu überwinden. Laut ART ist somit auch nichts mit Tunnel."

Warum sollte für ein Quant, eine unendlich hohe Potenzialbarriere ein Hindernis sein?
Das Quant muss diese Barriere nicht überwinden um von drinnen nach draußen zu kommen. Wenn sein Standort nicht 100% klar ist, ist es im extremfall per Zufall eben mal drinnen, mal draußen oder beides gleichzeitig. Es überwindet diese Barriere also nicht, sondern sein Standort ist per Definition nicht zwingend entweder innerhalb oder außerhalb.

Eine Frage noch: Für was steht ART?


Grüße
Marcus

Was für mich an der Kerr-Lösung unklar ist:

Kann sich ein eindimensionales Objekt überhaupt drehen?
Eindimensional bedeutet, dass es nur eine Koordinate, jedoch keine Ausdehnung gibt.
Etwas das keine Ausdehnung besitzt, hat keinen Radius oder Umfang und kann seine Lage in sich nicht verändern. Was sich aus meiner Perspektive drehen kann, ist die Umgebung des Schwarzen Lochs, also alles was sich zwischen der Koordinate, der Singularität, und dem Ereignishorizont befindet.

Daraus wiederum ergibt sich die Frage: Was gehört zum Schwarzen Loch?
Nur die Singularität als solche, oder alles bin hin zum Ereignishorizont?
Für mich ist die Frage im Grunde genommen beantwortet:
Der Ereignishorizont ist letztendlich nur die dreidimensionale Manifestierung der garvitativen Wirkung der Singularität.
Das heißt wenn man zur Singularität den kompletten Bereich innerhalb des EH hinzu zählte, wäre die Sigularität keine solche mehr, da der EH dreidimensional ist.

Somit steht meine Kernfrage: Kann sich ein eindimensionales Objekt überhaupt drehen?


Marcus

@Talax

Eindimensional ist z.B. eine Linie. Ein Schwarzes Loch ist dimensionslos. Zur Frage der Rotation: diese resultiert aus der Drehimpulserhaltung. Das Objekt, welches was zu einem schwarzen Loch kollabiert ist, bringt einen Drehimpuls mit. Jedes weitere Objekt, welches den EH überschreitet trägt mit seinem Drehimpuls ebenfalls zu dem des Schwarzen Loch bei.

Wikipedia: Drehimpuls

ornis schrieb:Das Objekt, welches was zu einem schwarzen Loch kollabiert ist, bringt einen Drehimpuls mit. Jedes weitere Objekt, welches den EH überschreitet trägt mit seinem Drehimpuls ebenfalls zu dem des Schwarzen Loch bei.

Ein Beispiel für so ein Objekt wäre ein Photon, was mit seinem Impuls zum Gesamt Impuls und somit zu m aber nicht M beitragen dürfte, wenn auch nur marginal.

@fritzchen1

Auch ein Elektron wird als punktförmige Ladung betrachtet, die "Größe" wird nur mit "kleiner als ..." angegeben. Das macht es ja auch zu einem Problem, denn die Ladung nimmt mit der Entfernung ab und demnach eben zu, wenn man diese halbiert und sich annähert. Somit strebt die gegen unendlich, je näher man einem Elektron kommt. Darum wird auch normiert und man postuliert virtuelle Positronen, welche als Wolke um das "nackte" Elektron entstehen und dessen Ladung abschirmen.

http://wissenschaft.marcus-haas.de/theorie/elektron.html
http://www-static.etp.physik.uni-muenchen.de/fp-versuch/node16.html
http://www.desy.de/~geiser/Lehre/WS0607/Masse4.pdf (Seite 3)

Je genauer man "hinschaut" und versucht etwas zu beschreiben um so komplexer wird die Beschreibung.

nocheinPoet schrieb:Je genauer man "hinschaut" und versucht etwas zu beschreiben um so komplexer wird die Beschreibung.

Tja und früher hat man immer gedacht es würde immer einfacher. Wenn man nur genau genug hinschauen kann.

Zusammen genommen sind ART und QT nach meinem geschmack viel zu komplex.

@ ornis
Das mit der Linie Stimmt, ist aber für die Singularität, ein gravitativ kollabiertes Objekt, keine zutreffende Beschreibung.
Es kann eigentlich nur ein Punkt ohne Maße, so wie ein Elektron sein.

@nocheinPoet
Durch die plankschen Einheiten, Planck Länge = 10 hoch -35m, ist der Teilbarkeit ein Ende gesetzt.

fritzchen1 schrieb: "Zusammen genommen sind ART und QT nach meinem geschmack viel zu komplex."
Als gelernter Schlosser bin ich geneigt dem zu zu stimmen. Doch was bitte ist ART? ;-)