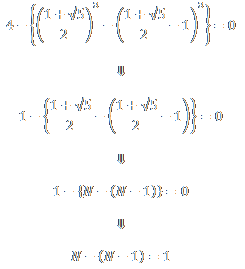@BlackFlame Herzlichen Dank für Deine überaus korrekten Ergänzungen!
Dass ich den positiven Wert von (1+sqrt5)/2 genommen habe, hängt damit zusammen, dass ich eine Verbindung ZUR PHYSIK gesucht habe, möglicherweise die 4-dimensionalität der Raumzeit mit Hilfe der Zahlentheorie - inbegriffen die "Zahl der Schönheit in der Natur", also Phi - etwas mehr als bloss "akzeptabel" erfassen zu können... ((Die Formel von BINET in Zusammenhang mit den Fibonacci-Zahlen "favorisiert" die Zahl 4 überhaupt nicht.))
Die Besonderheit "meiner Formel" sehe ich weiterhin darin, dass es NICHT NUR BEI x^3 "funktioniert", sondern AUCH bei Phi^p (p ist eine beliebige PRIMZAHL) "sehr-sehr häufig" ebenso eine PRIMZAHL erzeugt... Könntest Du mir, bitte, auch diesbezüglich etwas klärendes dazu mitzuteilen? Merci!
((Einige Beispiele dazu: bei p=11 bekommt man 199, bei p=17 dann 3571, bei p=29 dann 1149851=19*19489 um auch ein Gegenbeispiel zu nennen - aber leider wird mein Taschenrechner bei grösserer Primzahlen sehr schnell "müde"...))
Nochmals vielen dank
und herzliche Grüsse: Endre
PS.: Ach ja, fast vergessen! Wie ich die "Definition" von Null als quasi-transzendente Zahl gemeint habe. 1./ Ich weiss (immer noch) so, dass Phi eine transzendente Zahl ist - die einschlägige Literatut (welche ich kenne) vermittelt noch die BEWEISE dazu, dass es nicht so wäre... Vermutungen und triviale Manipulationen ((wie z.B. bei sqrt5-sqrt5=0 etc. "die Irrazionalität verschwindet" - nanà!!! ... etc.)) klingen nicht einmal wenig überzeugend...
FAZIT: Ich wollte DAS zum Ausdruck bringen, dass in "meiner Formel" die Zahlen 3 und 4 und Phi in gemeinsamer Verbindung vorkommen, wobei 3und 4 nicht, aber Phi (m.M.n) doch eine transzendente Zahl ist, so kann man das Resultat Null dieser "Gruppierung" als "quasi-transzendente Zahl" benennen. - Ich will aber keinesfalls "schizophrene Neubildungen" in die Diskussion einführen, also wenn jemand das als nicht-passend findet, kann ruhig vergessen... BLEIBEN WIR BEI DER ZAHLEN! E.