@Izaya Ich habe bereits gesagt nein, aber du musst dran denken, dass du mehr weißt, als der, der neu dazugekommen ist.
Nicht viel mehr. Ich weiß nur, dass es eine Option mit 2/3 WSK gibt. Ich weiß nur einfach nicht, hinter welcher Tür die sich diese Chance versteckt.
Noch ein Vergleich:
Stell Dir vor, Du sollst entscheiden, welches Fußballteam ein wichtiges Spiel bestreiten soll. A, B der C.
Der Trainer sagt Dir, dass nur eine Mannschaft gut ist, die anderen nicht. Er zeigt Dir, dass C Nieten und somit raus aus der Entscheidung sind.
Es bleiben A und B. Du weißt, ein Team davon ist super (höhere WSK), das andere miserabel.
Nun, wie entscheidest Du, ohne die Teams wirklich zu kennen? Nutzt Dir jetzt Dein Wissen, dass die einen doppelt so gut sind wie die anderen, wenn Du nicht weißt, ob das A oder B ist?
Nutzt es Dir, in letzter Sekunde Deine Meinung zu ändern, nur weil Du weißt, dass die einen doppelt so gut sind wie die anderen, Du aber immer noch nicht weißt, ob das jetzt A oder B ist?
Legen wir es jetzt mal wieder auf die Tür um, dann gibt es zwei Möglichkeiten: bei der Entscheidung bleiben oder wechseln.
Wir wirkt sich das aufs Ergebnis aus? Sagen wir, das Auto steht auch praktischerweise hinter Tür A. A ist somit die Tür mit der höheren WSK.
Variante 1: Du hast auf A getippt, wechselst nicht, und gewinnst.
Variante 2: Du hast auf B getippt, wechselst nicht, und verlierst.
Variante 3: Du hast auf B getippt, wechselst, und gewinnst.
Variante 4: Du hast auf A getippt, wechselst, und verlierst.
Ich hoffe, es ist jetzt klar genug, zu sehen, dass ein Wechsel nichts daran ändert, ob Du gewinnen oder verlieren wirst.
Warum gewinnt man also? Weil man die WSK richtig berechnet hat? Oder weil eben rein zufällig, die Tür A die mit der höheren WSK ist? Und weil man rein zufällig auf die Tür mit der höheren WSK getippt hat?
Das Auto hätte auch zufällig hinter Tür B stehen können. Die höhere WSK fürs Auto ändert nichts daran, wo es zufällig steht.
Und der Kandidat muss ja nur den Ort, wo dieses dolle gewinnträchtige Auto stehen könnte, also den Zufall, erraten, nicht die WSK, mit der das Auto hinter der gewählten Tür stehen könnte.
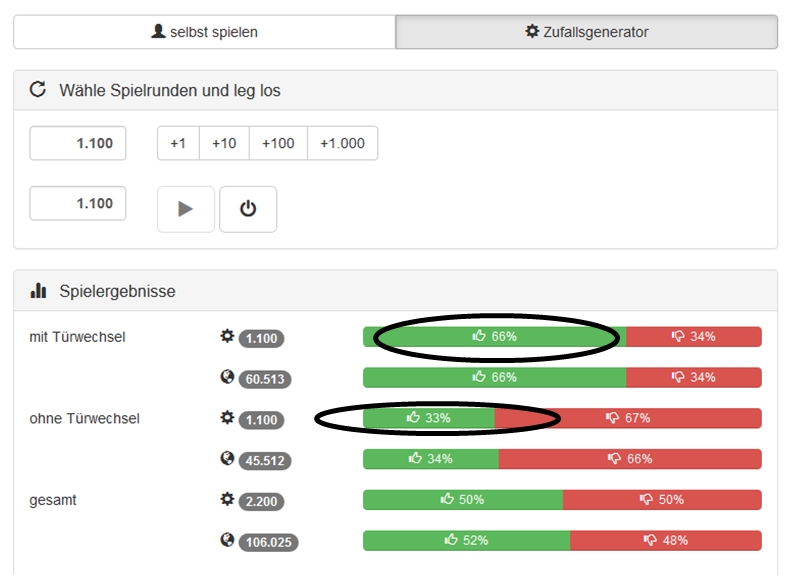
@Issomad Und bei 1000 Durchläufen ist es etwa 50 zu 50 ...
Danke. Das ist der Punkt, auf den ich hinaus will. Wenn ich mich zwischen nur mehr zwei Optionen entscheiden muss, liegt der Zufall, auch die richtige zu treffen, bei 50:50. Selbst, wenn die richtige Option zu 99% richtig ist.
@mojorisin Sonst habe ich nicht die notwendigen INformationen um die Wahrscheinlichkeit zu berechnen.
Die nutzen dir aber ohnedies nichts, weil Du nicht weißt, hinter welcher Tür sich diese erhöhte WSK befindet. Das Wissen darum, dass eine Tür tolle Chancen hat, die andere nicht, hilft nicht bei der Entscheidung, welche es denn wäre.
Deine Chance, die richtige Tür erwischen zu können, ist gestiegen, aber nicht durch den Wechsel Deiner Meinung. Ein Wechsel ist daher nicht besser als ein Bleiben.
Selbst, wenn Du wüsstest, dass eine Tür eine 99% Chance hat, die andere nur 1%, hättest Du keine Möglichkeit, im Vorfeld heraus zu finden, welche die mit der höheren WSK wäre.
Wie denn auch? Nur, weil Du die WSK ausgerechnet hast, springt das Auto doch nicht einfach genau hinter die Tür, die Du letztendlich wählst.