Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
574 Beiträge ▪ Schlüsselwörter:
Psychologie, Ziegenproblem, Wahrscheinlichkeiten ▪ Abonnieren: Feed E-Mail
mojorisin
Diskussionsleiter

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

dabei seit 2011
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 21:46Ich habe ein anderes Problem im Kopf welches allerdings mathematische ist und großes Kopfzerbrechen bereiten kann wenn man sich darauf einlässt. Man kann aber auch viel dabei lernen.kleinundgrün schrieb:Wie wäre es mit der Schildkröte als nächstes? Auch wenn das schon mal angerissen wurde. Es zeigt aber recht schön, wie ein kleiner Denkfehler ein Problem generieren kann.
Das Problem ist bekannt als Bertrand-Paradoxon, und ich bediene mich hier mal schamlos der Wikipedia:
Die Fragestellung ist folgende:
Wir betrachten einen Kreis und ein einbeschriebenes gleichseitiges Dreieck. Eine Kreissehne wird zufällig ausgewählt. Wie hoch ist die Wahrscheinlichkeit, dass die Sehne länger ist als eine Seite des Dreiecks?Wikipedia: Bertrand-Paradoxon (Wahrscheinlichkeitstheorie)
Ich hatte am Anfang Probleme das eigentlich Problem zu verstehen aber mit ein bisschen reinfuchsen geht es.
Hierzu jeztzt aber ein einfaches Bild:
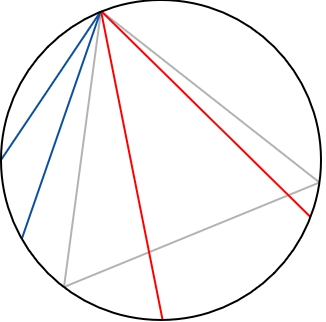
Die grauen Linien das Dreieck. Rot sind die Sehnen die länger sind als eine Seite vom Dreieck und Blau sind die die kürzer sind.
Jetzt kommt die eigentliche Frage: Wieviel Prozent aller Möglichen Sehnen sind länger als eine Seite vom Dreieck?
Wenn wir das obere Bild anschauen kommt Bertrand zu folgender Methode das Problem zu lösen:
Methode 1: zufällige EndpunkteOhne Frage klingt diese Antort schlüssig.
Zwei Punkte auf dem Kreisumfang werden zur Sehne verbunden. Um die Wahrscheinlichkeit zu berechnen, stellt man sich das Dreieck so gedreht vor, dass ein Eckpunkt mit einem der Endpunkte zusammenfällt. Liegt nun der andere Endpunkt der Sehne auf dem Segment des Umfangs, der zwischen den anderen beiden Eckpunkten des Dreiecks liegt, so ist die Sehne länger als die Dreiecksseite. Die Länge dieses Segments beträgt ein Drittel des Kreisumfangs, also ist die Wahrscheinlichkeit, dass die Sehne länger ist als die Dreiecksseite, gleich 1/3.
Allerdings gibt es eine weitere Möglichkeit die Fragestellung zu lösen:
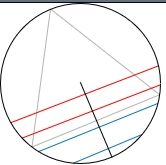
Methode 2: zufälliger RadiusEs gibt noch weitere Ansätze aber diese zwei sollen hier mal genügen.
Ein Radius und ein zufälliger Punkt auf dem Radius werden gewählt und die Sehne orthogonal zum Radius durch den Punkt gezogen. Um die Wahrscheinlichkeit zu berechnen, stellt man sich das Dreieck so gedreht vor, dass eine Seite orthogonal zum gewählten Radius liegt. Die Sehne ist länger als die Dreiecksseite, wenn der zufällig gewählte Punkt näher am Mittelpunkt des Kreises liegt als der Schnittpunkt der Dreiecksseite mit dem Radius. Die Dreiecksseite halbiert den Radius, also ist die Wahrscheinlichkeit, dass die Sehne länger ist als die Dreiecksseite, gleich 1/2.
ALso jetzt die Frage welches ist die richtige Lösung 1/3 oder 1/2? Beides kann ja nicht richtig sein?
perttivalkonen

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2012
dabei seit 2012
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 21:47Ja, das merk ich immer wieder beim Wahrscheinlichkeitsschätzen hiesiger User (vor allem neuer) in Sachen außerirdisches Leben. Vielen reicht ja schon das riesige Universum mitsamt den unzähligen Welten, daß außerirdisches Leben nicht nur ne Wahrscheinlichkeit, sondern recht eigentlich schon ne Gewißheit wäre. Andere schauen auf die Drake-Gleichung, sehen fünf Terme, und meinen dann ebenfalls, daß die Wahrscheinlichkeit doch nur hoch liegen könne, angesichts 100...400 Milliarden Sternen in unserer Galaxie.mojorisin schrieb:Bei Wahrscheinlichkeiten liegen wir aber oft extrem falsch obwohl wir überzeugt davon sind richtig zu liegen.
Natürlich bestehen die Terme in der Drakegleichung mehrheitlich aus zusammengefaßten Faktoren, deren Zahl deutlich höher als fünf liegt. Aber selbst fünfunddreißig Faktoren - für Lebensentstehung nicht grad hochgegriffen - kommen vielen so wenig vor, daß sie sich nicht vorstellen können, wie dadurch ne Wahrscheinlichkeit für Exoleben im gesamten sichtbaren Universum gegen Null gedrückt werden kann.
In Fällen wie diesen wird deutlich, daß das, was für "Intuition" gehalten wird, letztlich ideologischer Natur ist. Das, was ich gern hätte als Realität, das kommtmir plausibel vor, und das lenkt meine Einschätzung seiner Existenzwahrscheinlichkeit in die Höhe. Wenn ich etwas nicht glaube, dann schätze ich Wahrscheinlichkeiten hierfür natürlich auch eher nach unten ein. Rein "intuitiv".
Aber das ist nochmal was anderes als das menschliche Scheitern daran "sich Zahlen vorzustellen". Dürfte dennoch zum Thema passen.
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 21:58Nur weil es lediglich 2 Möglichkeiten gibt, ist die Chance nicht automatisch 50:50. Wirklich nicht.
Wenn man in 99% der Fälle draufgeht, dann ist die Chance daß man überlebt, eben nicht 50:50, sondern 1 in 100 oder 1:99.
Beispiel: der nächste Meteor kann Dir auf den Kopf fallen oder er kann Dir nicht auf den Kopf fallen. Dir fällt aber nicht jeder zweite Meteor auf den Kopf. Nicht 50:50
Wenn man in 99% der Fälle draufgeht, dann ist die Chance daß man überlebt, eben nicht 50:50, sondern 1 in 100 oder 1:99.
Beispiel: der nächste Meteor kann Dir auf den Kopf fallen oder er kann Dir nicht auf den Kopf fallen. Dir fällt aber nicht jeder zweite Meteor auf den Kopf. Nicht 50:50
perttivalkonen

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2012
dabei seit 2012
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
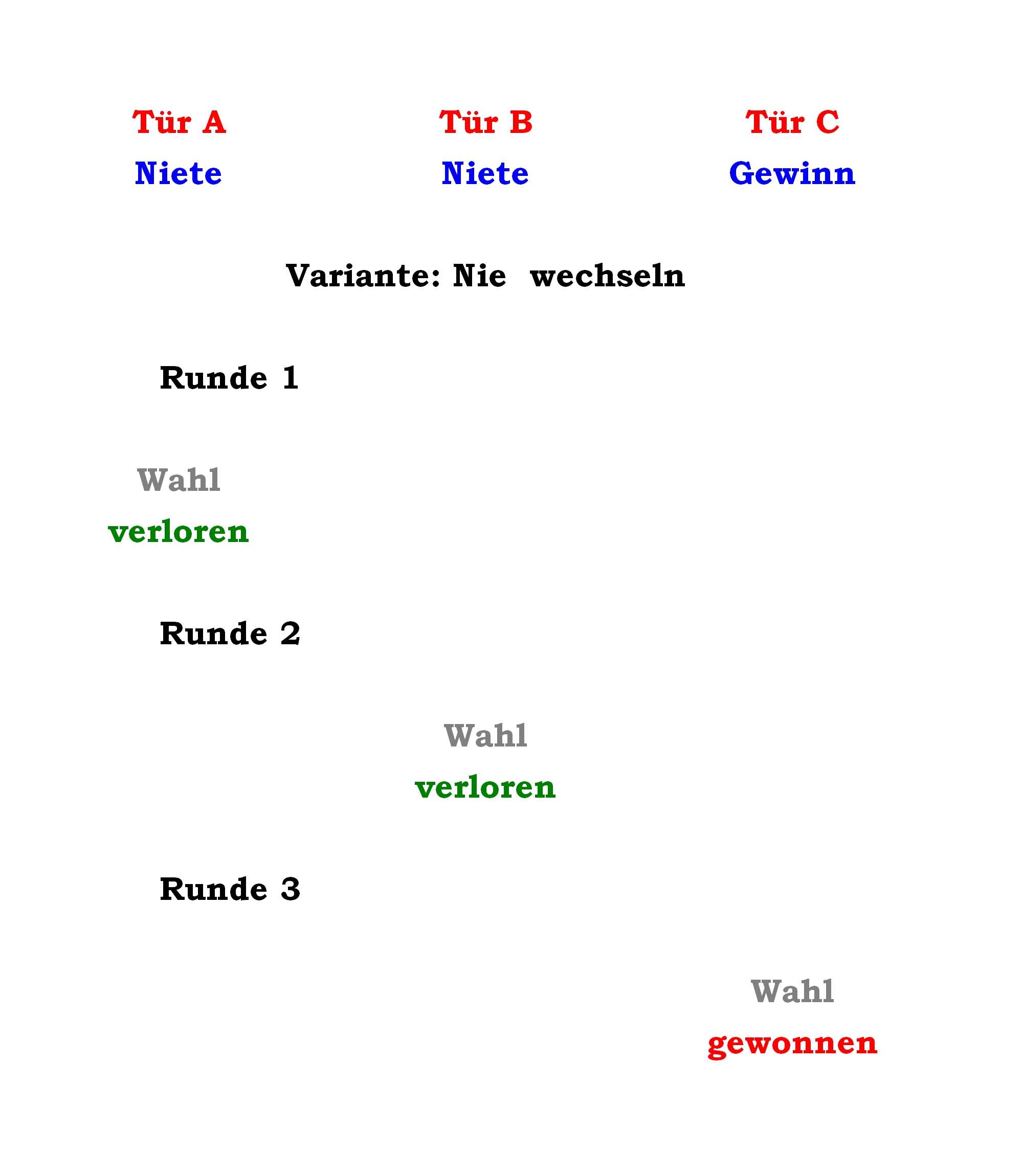
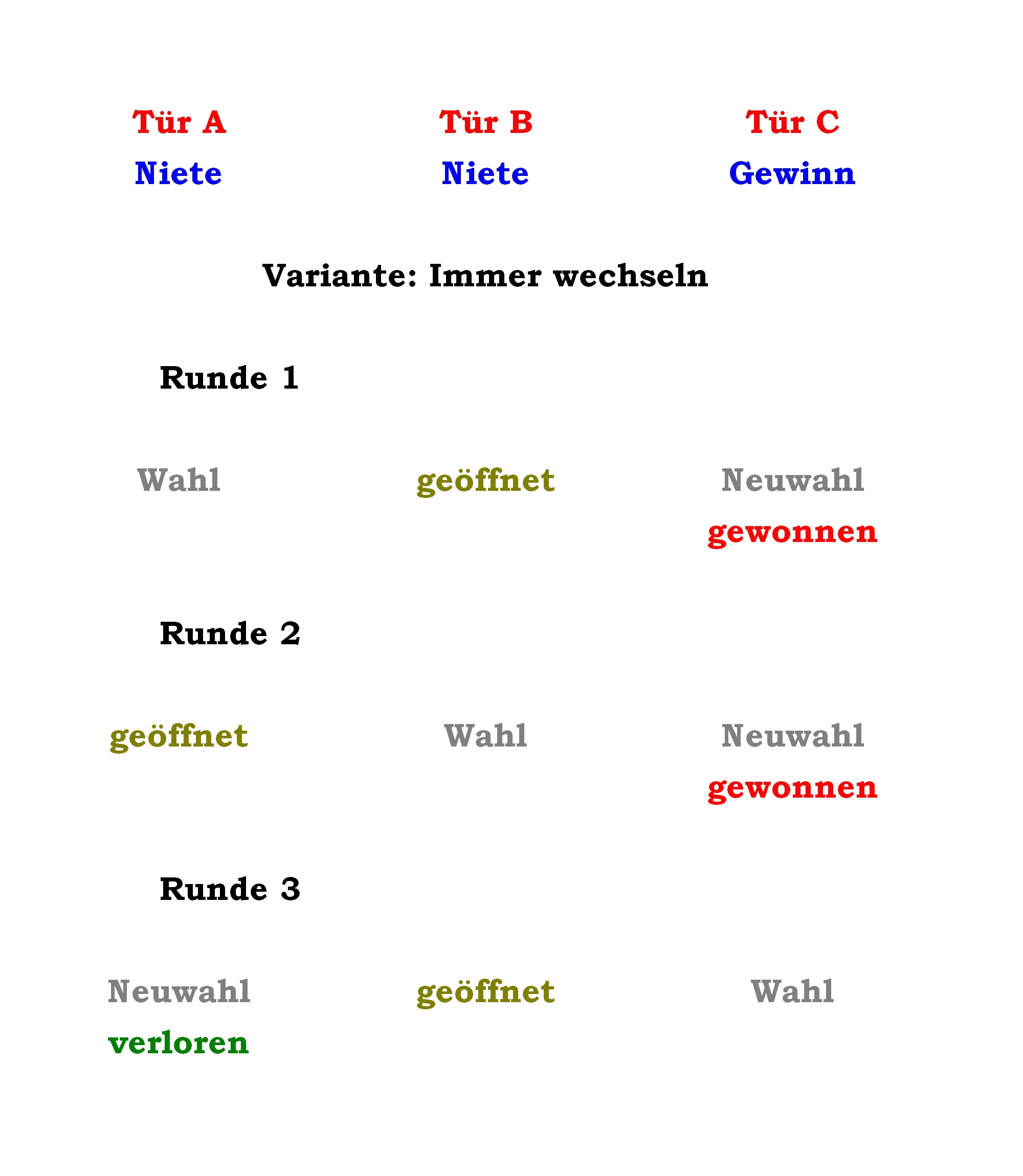
28.09.2018 um 22:18Weil sie nicht wegfällt. Als Du Dich entscheiden mußtest, war sie schließlich für Dich vorhanden. Deine Entscheidung fiel nun mal unter drei Türen.off-peak schrieb:Und im Übrigen fällt mir da gerade noch eine Betrachtung ein: Warum bitte, soll sich die Wahrscheinlichkeit erhöhen, dass das Auto getroffen wird, nur weil die dritte Option weg fällt?
Gerade wenn Du Dich von vornherein entscheidest, nicht zu wechseln, wird es deutlich. Wenn Du unbeirrbar bei Deiner ersten Wahl bleibst, dann ist es doch egal, ob der Showmaster nachträglich nochmal eine Tür öffnet oder nicht. Und wenn er keine Tür öffnet, dann leuchtet es doch selbst Dir ein, wieso Deine Gewinnchance nur 1:3 ist, oder?
Wenn Deine Gewinnchance dennoch immer bei 1:3 liegt, dann bleibt die Chance, mit beiden anderen Toren zusammen zu gewinnen (wenn man zwei Türen wählen dürfte), doch ebenfalls stets 2:3 hoch, oder?
Nun zeigt Dir der Showmaster aber freiwillig, daß hinter einer der beiden Türen nix ist. Wälke dennoch beide Türen, nimm also die 2:3-Wahrscheinlichkeit, und gib die offene Tür wieder ab, die mit der Wahrscheinlichkeit 0 (0:3). Wieviel Gewinnwahrscheinlichkeit also bleibt Dir?
Sieh es mal so. Du spielst drei mal. Du weißt jetzt schon, in zwei Spielen wirst Du verlieren mit Deiner Anfangswahl, und in einem Spiel wirst Du gewinnen. Richtig?
In den zwei Spielen, in denen Du mit der Erstwahl eine Nietentür gezogen hast, weißt Du, daß eine der verbleibenden Türen eine Niete verbirgt und eine den Hauptgewinn. In diesen beiden Fällen muß hinter der vom Showmaster nicht geöffneter Tür der Gewinn liegen. Nur in dem einen Fall, in dem Du die richtige Tür gewählt hast, weißt Du, daß hinter beiden anderen Türen nix ist, egal, welche der Spielleiter aufmacht.
Du weißt also, daß Du in zwei Fällen garantiert die Gewinntür erhältst, wenn Du wechselst, und nur in einem Falle nur ne Nietentür.
perttivalkonen

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2012
dabei seit 2012
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 23:00Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 23:07Ich bin kein Mathematiker (habe also eigentlich keine Ahnung), aber steht im Wikipedia-Artikel nicht:mojorisin schrieb:ALso jetzt die Frage welches ist die richtige Lösung 1/3 oder 1/2? Beides kann ja nicht richtig sein?
Das Bertrand-Paradoxon, benannt nach Joseph Bertrand (1822–1900),[1] in der Stochastik besagt, dass Wahrscheinlichkeiten nicht wohldefiniert sein müssen, wenn der zugrunde liegende Wahrscheinlichkeitsraum bzw. die Methode, die die Zufallsvariable von Interesse produziert, nicht eindeutig definiert ist.Wikipedia: Bertrand-Paradoxon (Wahrscheinlichkeitstheorie)
Das heißt doch, dass die Wahrscheinlichkeit nicht eindeutig sein muss (solange es die zugrunde liegende Methode, die Zufallsvariable zu bestimmen auch ist, was hier ja gegeben ist. Russel gibt ja mehrere Methoden vor).
Der Sinn des Paradoxons ist es also, keine Auflösung zu geben.
In der englischen Wikipedia steht noch ein wenig mehr. Edwin Jaynes behauptete (1973) wohl von sich, eine Lösung gefunden zu haben. Hierbei sagt er zunächst, dass man von nichts ausgehen darf, was nicht gegeben ist. Wir kennen also weder die Größe noch die Position des Kreises. Die Lösung muss also, sowohl bei Skalierung, also der Änderung der Größe, als auch bei der Translation, der Änderung der Position, unverändert bleiben. Das erfüllt nach Jaynes nur Methode 2. Wobei diese Argumentation wiederum in einem Artikel von 2015 angefochten wurde. Du hast dir also scheinbar ein aktuelles Problem aus dem Forschungsbereich ausgesucht... O_O
Die Sache ist, dass der Zufall nicht mehr wirklich gegeben ist, wenn ich das richtig verstanden habe. Wir haben ja diese Abbildungen, die sich ergeben, wenn man mit der respektiven Methode Sehnen findet:



Und das da scheinbar immer voneinander unterschiedliche Muster rauskommen, legt doch einen gewissen Determinismus, der jeder Methode innewohnt, nahe, oder?
Jedenfalls ein interessantes Problem von der Sorte, einfach zu verstehen, schwer zu lösen.
Es geht um den Gewinn!!!Peter0167 schrieb:Meiner Meinung nach gibt es 4 mögliche Scenarien, und nicht nur die 3.
Also, versessen auf das Auto, interessiert uns nur, wo das Auto steht.
- Hinter Tür 1
- Hinter Tür 2
- Hinter Tür 3
Das wars. Welche Tür unser Herr Moderator öffnet, ist uns ja eigentlich Schnuppe. Es geht uns darum, ob wir durch den Wechsel gewinnen oder verlieren.
Wir haben 1 gewählt.
Ist das Auto hinter 1 -> Wechsel ist ne Niete (Egal, welche Tür uns gezeigt wird)
Ist das Auto hinter 2 -> Wechsel ist ein Gewinn
Ist das Auto hinter 3 -> Wechsel ist ein Gewinn
Du hast recht, es gibt 4 Szenarien. Aber uns interessiert ja die Wahrscheinlichkeit, ein Auto zu bekommen, nicht die Wahrscheinlichkeit, ein Szenario zu bekommen. Wir schauen uns also an, wo ist ein Auto hinter und evaluieren, kriegen wir das beim Wechsel.
Und während ich hier vor mich hin tippe, wie eine Schildkröte, hat @perttivalkonen auch schon zwei Tabellen gebastelt, die vllt. mehr helfen, als meine Erkärung :D
perttivalkonen

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2012
dabei seit 2012
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 23:19Aber es ist doch einfach zu durchschauen.Peter0167 schrieb:Naja, wenn es so einfach zu durchschauen wäre, dann wäre es wohl kaum ein "Phänomen".
Schon seit Jahren - ach was, seit Jahrzehnten - vermute ich, daß manche Menschen Schwierigkeiten haben, sich mathematische Aufgabenstellungen visualisieren zu können. Das hier dürfte so ein Fall sein, wieso manche das als einfach zu durchschauen empfinden und manche nicht.
perttivalkonen

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2012
dabei seit 2012
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 23:35Auch das ist m.E: eine Frage des Visualisierens von mathematischen Aufgabenstellungen.
Drei alte Freunde aus Studienzeiten treffen sich mal wieder. Sie gehen in ein Restaurant und bestellen ne Flasche Sekt. Als die Kellnerin diese bringt, bezahlen sie sofort: 30 Euro. Jeder legt nen Zehner auf den Tisch. Die Chefin siehts und sagt der Kellnerin "Die trinken sicher noch was danach, bring denen mal 5€ als Rabatt zurück". Die Kellnerin tuts. Sie legt den dreien fünf einzelne Euronen auf den Tisch. Jeder nimmt eins, bleiben zwei über. "Was solls", sagen sich die drei, und überlassen die zwei Münzen der Kellnerin. Während diese zurückgeht, denkt sie "Jetzt haben alle drei 10€ bezahlt und 1€ zurückbekommen; das sind 27€ Bezahlung. Ich hab nochmals 2€, macht 29. Wo ist der dreißigste Euro?"
Drei alte Freunde aus Studienzeiten treffen sich mal wieder. Sie gehen in ein Restaurant und bestellen ne Flasche Sekt. Als die Kellnerin diese bringt, bezahlen sie sofort: 30 Euro. Jeder legt nen Zehner auf den Tisch. Die Chefin siehts und sagt der Kellnerin "Die trinken sicher noch was danach, bring denen mal 5€ als Rabatt zurück". Die Kellnerin tuts. Sie legt den dreien fünf einzelne Euronen auf den Tisch. Jeder nimmt eins, bleiben zwei über. "Was solls", sagen sich die drei, und überlassen die zwei Münzen der Kellnerin. Während diese zurückgeht, denkt sie "Jetzt haben alle drei 10€ bezahlt und 1€ zurückbekommen; das sind 27€ Bezahlung. Ich hab nochmals 2€, macht 29. Wo ist der dreißigste Euro?"
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
28.09.2018 um 23:52Das glaube ich auch. Es muss an unterschiedlichen (nicht richtigen oder falschen!) Denkweisen liegen, sonst wären die Diskussionen darüber nicht so ellenlang.perttivalkonen schrieb:Schon seit Jahren - ach was, seit Jahrzehnten - vermute ich, daß manche Menschen Schwierigkeiten haben, sich mathematische Aufgabenstellungen visualisieren zu können. Das hier dürfte so ein Fall sein, wieso manche das als einfach zu durchschauen empfinden und manche nicht.
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 00:14Kleiner Nachtrag zu Bertrands Paradox. ( @mojorisin )
Habe ich glatt den Wikipedia-Artikel nicht fertig gelesen. Gibt noch einen Abschnitt "Recent developement".
Darin wird ein Paper von 2014 erwähnt, das einen neuen Ansatz hat. Erstmal möchte man die Frage wohldefiniert (well-posed*) haben, um sie dann vernünftig angehen zu können. Das erste woran man dabei denkt ist das "zufällig", welches erstmal definiert werden müsste. Das sehen die Autoren jedoch nicht als Quelle der Ungenauigkeit, sondern die undefinierte Natur des "Dings", dass man auswählt. Ist es eine Gerade, zwei Punkte oder ein Punkt und eine Gerade? Mit all dem ließe sich eine Sehne formen:
Dann hat man ein wohldefiniertes Problem und kann wohldefinierte Wahrscheinlichkeiten berechnen. Nun, was ist dabei die Problemstellung? Jetzt kommt das zufällig ins Spiel. Wie genau wählt man eigentlich die Sehne? Das macht das ganze dann ja irgendwie aus. Also berechnet man am Ende nicht irgendein Durchschnitt aller möglichen Sehnen, sondern aller möglichen Verfahren, eine Sehne festzulegen. Die Autoren nennen das "universal average", also universeller Durchschnitt.
Um das dann genauer zu erklären, müsste ich die Mathematik dahinter verstehen, was ich nicht tue. Also hört meine Erklärung hier auf. Wer neben der magischen 42 noch andere unverständliche Antworten haben möchte:
Mit der ersten Definition ist die Antwort: 1/2
Im zweiten Fall: 1/3
Mit der dritten Definition: 1/4
(Was alle Lösungen sind, die Bertrand errechnet hat. Was ein Zufall)
Wobei der Sinn des Paradoxons, zu veranschaulichen, dass ein nicht wohldefiniertes Problem keine eindeutige Lösung hat, durch die Aufteilung in mehrere wohldefinierte Probleme nicht mehr wirklich gegeben ist. Irgendwo schade. Tja.
Habe ich glatt den Wikipedia-Artikel nicht fertig gelesen. Gibt noch einen Abschnitt "Recent developement".
Darin wird ein Paper von 2014 erwähnt, das einen neuen Ansatz hat. Erstmal möchte man die Frage wohldefiniert (well-posed*) haben, um sie dann vernünftig angehen zu können. Das erste woran man dabei denkt ist das "zufällig", welches erstmal definiert werden müsste. Das sehen die Autoren jedoch nicht als Quelle der Ungenauigkeit, sondern die undefinierte Natur des "Dings", dass man auswählt. Ist es eine Gerade, zwei Punkte oder ein Punkt und eine Gerade? Mit all dem ließe sich eine Sehne formen:
- Gerade -> Sehne
- Zwei Punkte -> Gerade durch zeichnen -> Sehne
- Punkt und Gerade -> Gerade mit dem Punkt als Mittelpunkt -> Sehne
Dann hat man ein wohldefiniertes Problem und kann wohldefinierte Wahrscheinlichkeiten berechnen. Nun, was ist dabei die Problemstellung? Jetzt kommt das zufällig ins Spiel. Wie genau wählt man eigentlich die Sehne? Das macht das ganze dann ja irgendwie aus. Also berechnet man am Ende nicht irgendein Durchschnitt aller möglichen Sehnen, sondern aller möglichen Verfahren, eine Sehne festzulegen. Die Autoren nennen das "universal average", also universeller Durchschnitt.
Um das dann genauer zu erklären, müsste ich die Mathematik dahinter verstehen, was ich nicht tue. Also hört meine Erklärung hier auf. Wer neben der magischen 42 noch andere unverständliche Antworten haben möchte:
Mit der ersten Definition ist die Antwort: 1/2
Im zweiten Fall: 1/3
Mit der dritten Definition: 1/4
(Was alle Lösungen sind, die Bertrand errechnet hat. Was ein Zufall)
Wobei der Sinn des Paradoxons, zu veranschaulichen, dass ein nicht wohldefiniertes Problem keine eindeutige Lösung hat, durch die Aufteilung in mehrere wohldefinierte Probleme nicht mehr wirklich gegeben ist. Irgendwo schade. Tja.
Korrektur: Bertrand hat es vorgegeben. Nicht Bertrand Russel, sondern Joseph Bertrand! Mein Fehler! Ist zu spät :DIzaya schrieb:Russel
mojorisin
Diskussionsleiter

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

dabei seit 2011
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 10:03@Izaya
Die Frage war ja:
Das Problem ist die Größe der einzelnen Mengen zu bestimmen. Da die Menge aller Sehnen unendlich ist und ebenso die Menge aller Längeren Sehnen hat man es mit zwei unendlichen Mengen zu tun.
Das Paradoxon für die unterschiedlichen Methoden taucht auf weil wir in die obere Formel jeweils nur Teilmengen der Möglichen Sehnen eintragen.
Leider ist das Paradoxon etwas abstrakt und mathematisch dennoch mag ich es denn es zeigt wie einfach man zu vermeintlich richtigen Lösungen kommen kann ohne das diese auch richtig sein müssen
Danke für den Link. ICh werde es mir mal in Ruhe durchlesen. Der Punkt in dem Paradoxon, den ich interessant finde ist der das man zu einer Lösung eines Problems gelangen kann über eine Methode, die absolut fundiert und richtig erscheint und man daher auch überzeugt ist das man richtig gerechnet hat, aber dann doch falsch sein muss.Izaya schrieb:Wobei der Sinn des Paradoxons, zu veranschaulichen, dass ein nicht wohldefiniertes Problem keine eindeutige Lösung hat, durch die Aufteilung in mehrere wohldefinierte Probleme nicht mehr wirklich gegeben ist. Irgendwo schade. Tja.
Die Frage war ja:
We draw at random a chord onto a circle. What is the probability that it is longer than the side of the inscribed equilateral triangle?Und diese Frage scheint so simpel das sie auch beantwortbar sein muss. Das Problem ist hier also tatsächlich nicht die finale Lösung zu berechnen was ganz einfach wäre:
P = \frac{Menge~aller~längeren~Sehnen}{Menge~aller~Sehnen}
Das Problem ist die Größe der einzelnen Mengen zu bestimmen. Da die Menge aller Sehnen unendlich ist und ebenso die Menge aller Längeren Sehnen hat man es mit zwei unendlichen Mengen zu tun.
Das Paradoxon für die unterschiedlichen Methoden taucht auf weil wir in die obere Formel jeweils nur Teilmengen der Möglichen Sehnen eintragen.
Leider ist das Paradoxon etwas abstrakt und mathematisch dennoch mag ich es denn es zeigt wie einfach man zu vermeintlich richtigen Lösungen kommen kann ohne das diese auch richtig sein müssen
mojorisin
Diskussionsleiter

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

dabei seit 2011
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 10:09Nun ein kleines Rätsel das ich selbst erst heute morgen aufgeschnappt habe:
Angenommen es gibt gleich viele Mädchen wie Jungen. Mit diesem Wissen ausgestattet treffen wir eines Tages eine Vater mit seinem Sohn auf der Straße und er erzählt uns das er zwei Kinder hat.
Wie groß ist die Wahrscheinlichkeit das er zwei Söhne hat?
Angenommen es gibt gleich viele Mädchen wie Jungen. Mit diesem Wissen ausgestattet treffen wir eines Tages eine Vater mit seinem Sohn auf der Straße und er erzählt uns das er zwei Kinder hat.
Wie groß ist die Wahrscheinlichkeit das er zwei Söhne hat?
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:05Auskombiniert ergeben sich vier Möglichkeiten; da er aber mit einem Sohn unterwegs ist, scheidet eine (zwei Töchter) schon mal prinzipiell aus.
Bleiben noch drei Möglichkeiten, also ist die Wahrscheinlichkeit 1/3.
Bleiben noch drei Möglichkeiten, also ist die Wahrscheinlichkeit 1/3.
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:12Ich kenne das sehr gut von Sportwetten, nehmen wir an ich mache eine 5er Kombi in der alle 5 Tpps richtig sein müssen um zu gewinnen. Sagen wir die höchste Quote beträgt 2.0, die andere 1.80, zwei 1.50 und die niedrigste 1.10.
Die niedrigste nehm ich deswegen rein weil ich mir bei dieser zu 100% sicher bin das sie auch kommt und um den Gewinn zu steigern.
Nun sind es aber komischerweise oftmals solche Tipps die nach hinten los gehen da auch bei dieser 1.10 Quote trotzdem noch eine hohe wahrscheinlichkeit besteht das diese nicht aufgeht, daher lasst solchen Unsinn wie Lotto Spielen oder Glückspiele. Die lachenden sind nämlich am Ende die Anbieter die seit Jahren wie Pilze aus dem Boden sprießen weil jeder von sich behauptet er könne Hellsehen oder Wahrscheinlichkeiten bestimmen...
Die niedrigste nehm ich deswegen rein weil ich mir bei dieser zu 100% sicher bin das sie auch kommt und um den Gewinn zu steigern.
Nun sind es aber komischerweise oftmals solche Tipps die nach hinten los gehen da auch bei dieser 1.10 Quote trotzdem noch eine hohe wahrscheinlichkeit besteht das diese nicht aufgeht, daher lasst solchen Unsinn wie Lotto Spielen oder Glückspiele. Die lachenden sind nämlich am Ende die Anbieter die seit Jahren wie Pilze aus dem Boden sprießen weil jeder von sich behauptet er könne Hellsehen oder Wahrscheinlichkeiten bestimmen...
perttivalkonen

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2012
dabei seit 2012
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:25Nicht ganz 1:3.mojorisin schrieb:Wie groß ist die Wahrscheinlichkeit das er zwei Söhne hat?
1/3, weil es
a) nur vier Kombinationen bei zwei Kindern gibt: MM, MF, FM, FF, ferner weil
b) bei gleich viel M wie F jede Kombination gleich häufig vorkommen kann, und
c) weil die Gruppe FF ausfällt,
aber etwas weniger als 1:3, weil
d) der Vater ein Mann ist und damit die Menge der als Söhne in Frage kommenden männlichen Wesen um eins kleiner ist als die Menge der Frauen.
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:25Wir können ja mal einen heutigen Test machen, ich gebe 5 Spiele vor wo jeweils ein Favorit dabei ist, und jeder gibt mal seinen Tipp dazu ab, zur Auswahl stehen die Option Heimsieg (1) Unentschieden (X) und Auswärtssieg (2). Hier nun die Spiele:
Schalke - Mainz 1
Arsenal - Watford 1
Huddersfield - Tottenham 2
Juventus - Napoli 1
Real Madrid - Atletico Madrid X
Laut den Namen/Martkwert her müssten eigentlich alle Tipps so kommen wie ich Ausgewählt habe. Ich sage aber das wird nicht so Passieren!
Schalke - Mainz 1
Arsenal - Watford 1
Huddersfield - Tottenham 2
Juventus - Napoli 1
Real Madrid - Atletico Madrid X
Laut den Namen/Martkwert her müssten eigentlich alle Tipps so kommen wie ich Ausgewählt habe. Ich sage aber das wird nicht so Passieren!
mojorisin
Diskussionsleiter

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

dabei seit 2011
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:29@perttivalkonen
Ok die Logik kann ich nicht ganz nachvollziehen. Was wenn ich denselben Sohn abends mit seiner Mutter treffe. Ist dann die Wahrscheinlichkeit der Geschlechter der Kinder etwas größer 1/3?perttivalkonen schrieb:aber etwas weniger als 1:3, weil
d) der Vater ein Mann ist und damit die Menge der als Söhne in Frage kommenden männlichen Wesen um eins kleiner ist als die Menge der Frauen
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:32Nur wenn der Vater sein eigener Bruder ist, dann sollte man aber dringend mal mit der Mutter reden.mojorisin schrieb:Ok die Logik kann ich nicht ganz nachvollziehen. Was wenn ich denselben Sohn abends mit seiner Mutter treffe. Ist dann die Wahrscheinlichkeit der Geschlechter der Kinder etwas größer 1/3?
Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel
29.09.2018 um 11:33... oder gar sein eigener Sohn, dann müsste Oma Rede und Antwort stehen.towel_42 schrieb:Nur wenn der Vater sein eigener Bruder ist, dann sollte man aber dringend mal mit der Mutter reden.
Ähnliche Diskussionen
Das "Ziegenparadoxon" - anschauliche, einfache Lösung:
Transpersonale Psychologie u. ihre Begründer
Könntest du den Avatar des Users über dir in echt freimütig küssen?
Manipulieren Parasiten die Psyche eines Menschen?
In wie fern ist in der Neurologie die Pansexualität genau erklärbar?
Vollständige Heilung der Psyche möglich?
Aphantasie: fehlendes visuelles Vorstellungsvermögen