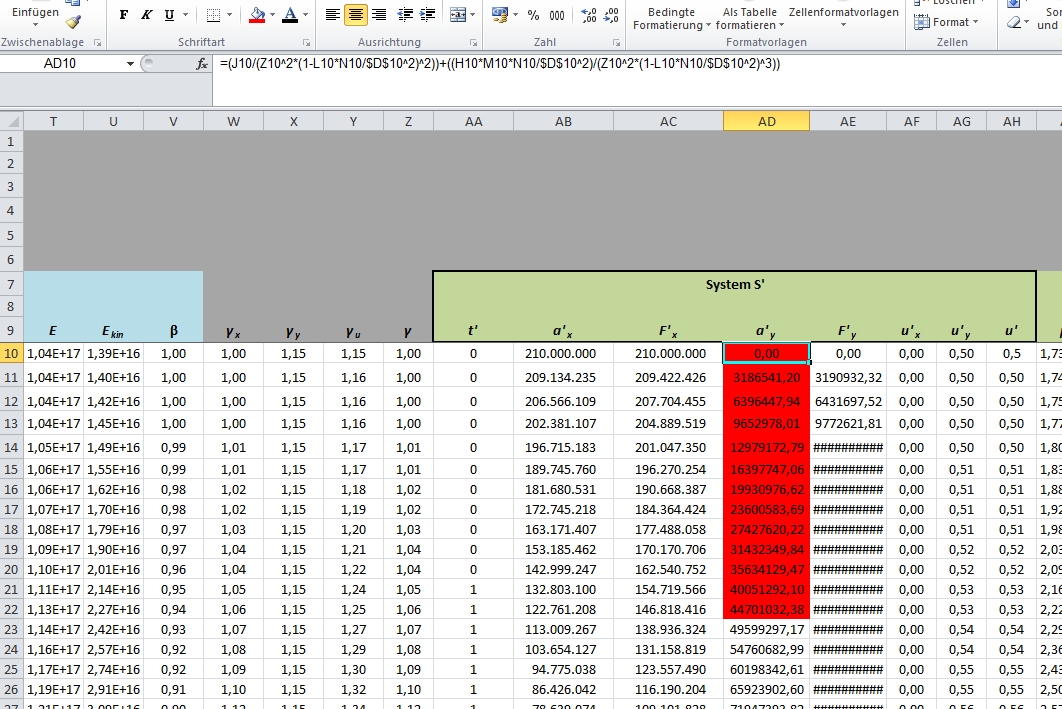
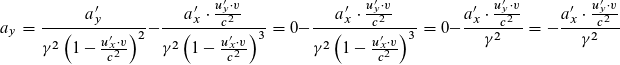mojorisin schrieb am 20.01.2018:Also während deine Werte aus den Spalten AH und AA ein extreme Beschleunigung ergeben setzt du a'y einfach = 0. DAs ist es was ich zuerst mal kritisiere.
mojorisin schrieb am 20.01.2018:Also während deine Werte aus den Spalten AH und AA ein extreme Beschleunigung ergeben setzt du a'y einfach = 0. DAs ist es was ich zuerst mal kritisiere.
Ok, und was ist mit der Tatsache das das auch bei deiner Excel-Tabelle der Fall ist?
Das einzige was du festgestellt hast ist, das meine Ergebnisse nicht mit deinen Erwartungen übereinstimmen. Die Schlussfolgerung daraus kann nur lauten;
Entweder sind meine Ergebnisse, oder aber deine Erwartungen fehlerbehaftet.Du erweckst aber den Eindruck, als könnte für dich nur der erste Halbsatz zutreffen.
 mojorisin schrieb am 20.01.2018:WEnn du recht hättest das a'y = 0 wäre, dann würde sich auch u'y nicht ändern denn nur dann ergäbe obige Formel:
mojorisin schrieb am 20.01.2018:WEnn du recht hättest das a'y = 0 wäre, dann würde sich auch u'y nicht ändern denn nur dann ergäbe obige Formel:
Mir ist ehrlich gesagt nicht ganz klar worauf du hinaus willst. Möchtest du zum Ausdruck bringen das das Konzept "Geschwindigkeiten sind relativ" nicht zutreffend ist?
Wenn du feststellen möchtest ob sich die Geschwindigkeit der Kugel verändert, sollte man zunächst andere mögliche variablen aus deiner Gleichung eliminieren. In unserem Fall wäre es der Lorentzfaktor, der ja ansteigt weil auf der
x-Achse eine Beschleunigung stattfindet und die
x-Achse als Relativgeschwindigkeit definiert wurde.
Wir sind uns einig das auf der
y-Achse keine Längenkontraktion erfolgt, es also gilt
y'=y ?
Wir sind uns auch einig das
t'= \frac t \gamma gilt ?
Wenn dem so sein sollte, was wird dann aus deiner Gleichung
\Delta {u_y'}=AG35-AG34 ?
Etwa nicht:
\Delta {u_y'}= \frac {AG35} {\gamma \left ( =W35 \right )}- \frac {AG34} {\gamma \left ( =W34 \right )}= \frac {0{,}609} {1{,}217}- \frac {0{,}602} {1,204}=0
Dann schauen wir doch mal wie du fortfährst:
 mojorisin schrieb am 20.01.2018:WEnn du recht hättest das a'y = 0 wäre, dann würde sich auch u'y nicht ändern denn nur dann ergäbe obige Formel:
mojorisin schrieb am 20.01.2018:WEnn du recht hättest das a'y = 0 wäre, dann würde sich auch u'y nicht ändern denn nur dann ergäbe obige Formel:
a_y'= \frac {\Delta u_y'} {\Delta t'}= \frac {0} {\Delta t'}=0
\Delta u_y' ist bei dir aber nicht null da sich u'y ändert.
Wie oben nachvollziehbar belegt, ist bei mir
a_y'=0 obwohl sich
u_y' ändert. Eben weil Geschwindigkeiten relativ, Beschleunigungen (in der SRT) jedoch absolut sind. Deshalb stehen meine Ergebnisse auch nicht im Widerspruch, sondern im Einklang mit der SRT.
Oder eben wenn die Kugel mit
u_y=0{,}5c die Strecke zwischen den Dedektoren
y=0{,}5Ls bei einer Relativgeschwindigkeit
v_{rel}=0{,}7c durchlaufen hat:
t= \frac {y} {u_y}= \frac {0{,}5Ls} {0{,}5c}=1s
u_y= \frac y t= \frac {0{,}5Ls} {1s}=0{,}5c
und für das gestrichene System gilt:
y'=y=0{,}5Ls
\gamma = \frac {1} {\sqrt {1- \frac {v_{rel}^2} {c^2}}}= \frac {1} {\sqrt {1- \frac {0{,}7c^2} {1c^2}}}=1{,}4
t'= \frac {t} {\gamma}= \frac {1s} {1{,}4}=0{,}714s
u_y'= \frac {y'} {t'}= \frac {0{,}5Ls} {0{,}714s}=0{,}7c
Oder eben über die Lorentz-Transformation:
u_y'=\frac {\sqrt {1- \left ( \frac {v^2} {c^2} \right )}u_y} {1- \frac {v} {c^2}u_x}=\frac {\sqrt {1- \left ( \frac {0{,}7c^2} {1^2} \right )}0{,}5c} {1- \frac {0{,}7c} {1^2}0{,}7c}=0{,}7c
nocheinPoet schrieb:Totaler Schwachsinn was Du hier weiter fabulierst.