Schwarze Löcher

mojorisin schrieb:Wenn jetzt hier die Masse gegen 0 geht dan nerhählt man die flache Minkowski Metrik.

Das heißt die flache Minkowski Raumzeit erhählt man genau dann wen keine Masse vorhanden ist, bzw m --> 0 geht.

Danke für die Erläuterungen! :)

Genau genommen ist es sogar noch strenger, wenn ich mich recht erinnere: Die Vakuumlösungen gelten im Fall von Kerr- und Schwarzschild-Metrik eigentlich nur dann, wenn das Schwarze Loch das einzige Objekt im gesamten Universum ist...

hawak schrieb:Kurz gesagt ging es mir darum, darauf hinzuweisen, dass die Vakuumlösungen allesamt Konstruktionen sind, die in der Realität nicht anzutreffen sind und daher meines Erachtens wenig geeignet sind, ein Gebilde wie ein SL (das ist hier das Thema) zutreffend zu beschreiben.

Ok, wenn das gemeint ist... Da gebe ich dir bzgl. Vakuumlösung natürlich recht. Siehe auch meine Antwort an mojorisin. Es ging ja aber auch ganz allgemein darum, ob die Feldgleichungen Lokalität zulassen.

hawak schrieb:Ebenso sind die Annahmen von Punktladungen (oder -Massen) eine Vereinfachung, die genauso wie die angenommene Flachheit der Raumzeit in hinreichend kleinen (lokalen) Gebieten sicherlich für bestimmte Betrachtungen ihre Berechtigung haben, aber im Umfeld eines SL‘s vollkommen fehl am Platze sind.

Die Argumentation, dass die Raumzeit doch "eigentlich" nicht flach ist schwingt hier bei einigen mit. Und das trifft es eben nicht.

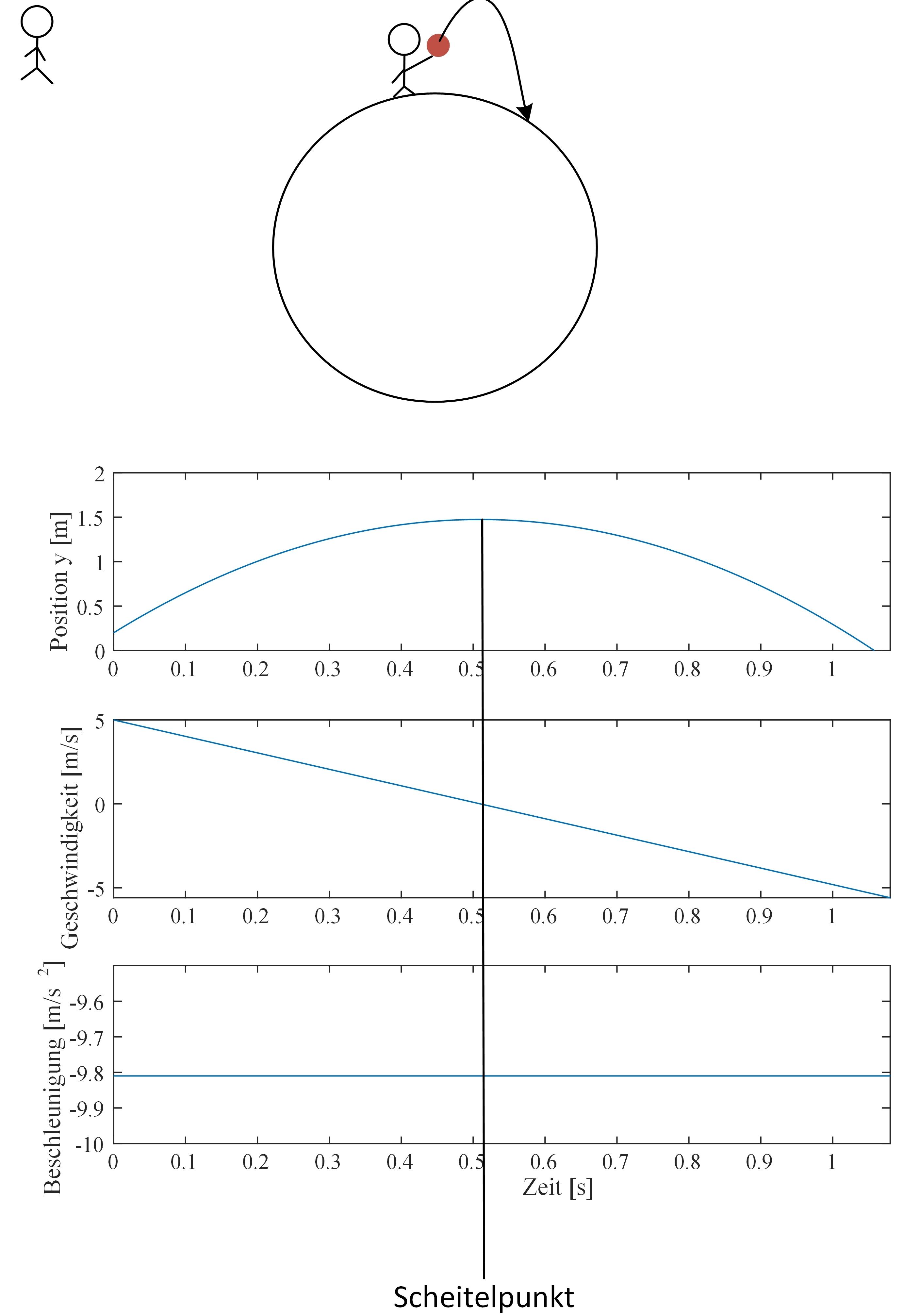
Noch mal zum Scheitelpunkt des Balls: Es gibt ein Bezugssystem im freien Fall (d.h. im Sinne der ART ein Inertialsystem), das äquivalent zum Bezugsystems des Balls am Scheitelpunkt ist. Das sagt doch eigentlich schon alles, die Raumzeit muss hier aufgrund des Äquivalenzprinzips flach sein. Und ein solches Bezugssystem wirst du z.B. auch vor dem Ereignishorizont eines Schwarzen Lochs finden. Nur dass die Fläche, in der die Raumzeit flach ist, hier sicher irgendwo auf Staubkorn-Niveau ist...

Vielleicht noch mal zwei andere Beispiele:

Sobald elektromagnetischen Wellen eine Rotverschiebung von z = sehr groß (z.B. 10.000 oder noch größer) erreichen, sind sie weg. Auch wenn sie rein theoretisch nie weg sind.

Ich glaube auch kaum, dass irgendjemand das Universum warm nennen würde, nur weil wir eine kosmische Mikrowellenhintergrundstrahlung mit einer Temperatur von ca. 2,3 K und z = ca. 1000 messen.

Wie gesagt: Es riecht wie ein Apfel, es schmeckt wie ein Apfel, es sieht aus wie ein Apfel - was ist es? Ein Apfel.

hawak schrieb:Das beobachtbare Universum ist weder exakt flach noch ist es von einander unabhängigen Punktladungen bevölkert.

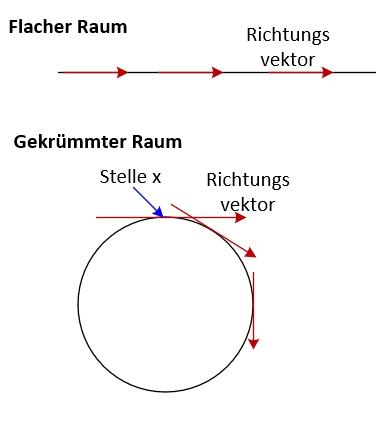
Das Universum könnte leicht gekrümmt sein. Wobei die Flachheit des Universums jetzt ja nicht direkt etwas damit zu tun hat, ob die Raumzeit lokal flach sein kann oder nicht...

PS.: Sorry, dass ich bzgl. der Frage "Wie definierst du lokal?" kurz die Nicks durcheinander geworfen hatte... ;)

@Arrakai

Arrakai schrieb:Noch mal zum Scheitelpunkt des Balls: Es gibt ein Bezugssystem im freien Fall (d.h. im Sinne der ART ein Inertialsystem), das äquivalent zum Bezugsystems des Balls am Scheitelpunkt ist. Das sagt doch eigentlich schon alles, die Raumzeit muss hier aufgrund des Äquivalenzprinzips flach sein.

Ich verstehe nicht was am Scheitelpunkt ausgezeichnet sein soll: Ein Beobachter der in einer BlackBox eingeschlossen die sich im Parabelflug befindet, kann nicht unterscheiden ob er sich im freien Fall befindet oder in der flachen Raumzeit (Gezeitenkräfte aufggrund inhomogner Felder mal außen vor). Insbesondere merkt er aber während des freien Falls keinen Unterschied ob er sich am Anfang, am Scheitelpunkt oder am Ende der FLugbahn befindet. Was also mach deiner Anischt nach den Scheitelpunkt der Flugbahn so ausgezeichnet?

Meiner Meinung nach ist für ihn in seiner BlackBox die Raumzeit solange quasi flach, solange er sich im freien Fall befindet.

mojorisin schrieb:Ein Beobachter der in einer BlackBox eingeschlossen die sich im Parabelflug befindet, kann nicht unterscheiden ob er sich im freien Fall befindet oder in der flachen Raumzeit (Gezeitenkräfte aufggrund inhomogner Felder mal außen vor).

Beim Parabelflug wird der Beobachter im Sinne der Klassischen Mechanik schwerelos, weil Zentripetal- und Schwerkraft sich genau aufheben. Im Fall der ART befindet er sich einfach im freien Fall, die Raumzeit ist für ihn lokal flach. Das gilt aber nicht für den ganzen Flug, sondern nur für eine gewisse Zeit.

Daher ist das vergleichbar mir dem Ball. Dort ist es...

mojorisin schrieb:Was also mach deiner Anischt nach den Scheitelpunkt der Flugbahn so ausgezeichnet?

… der Scheitelpunkt, an dem sich der Ball für einen kurzen Moment im freien Fall befindet. Daher ist dieser Punkt für den Ball ein ausgezeichneter Punkt.

mojorisin schrieb:Meiner Meinung nach ist für ihn in seiner BlackBox die Raumzeit solange quasi flach, solange er sich im freien Fall befindet.

Solange er sich selbst im freien Fall ist, sehe ich das genauso. Ist er natürlich nicht die ganze Zeit...

@Arrakai

Arrakai schrieb:Das gilt aber nicht für den ganzen Flug, sondern nur für eine gewisse Zeit.

Doch das gilt für den ganzen Flug. Solange keine Kräfte wirken, befindet man sich auf der Geodäte.

Arrakai schrieb:… der Scheitelpunkt, an dem sich der Ball für einen kurzen Moment im freien Fall befindet. Daher ist dieser Punkt für den Ball ein ausgezeichneter Punkt.

Der Ball befindet sich aber im freien Fall solange er keine Kräfte spürt, d.h. sobald er die Hand verlässt und bevor er auf dem Boden aufkommt.

Du kannst das selbst ausprobieren auf dem Trampolin: Sobald du den Boden verlässt fühlst du dich schwerelos solange bis du wieder auf dem Boden aufkommst. Nicht nur am Scheitelpunkt.

Peter0167 schrieb:Mit Ausnahme des "Punktes", in dem die Masse konzentriert ist.

Ja, da hast du natürlich recht. Ich hatte zwar auch schon gegenteiliges gelesen, aber so richtig überzeugend finde ich das nicht (mehr)...

mojorisin schrieb:Doch das gilt für den ganzen Flug. Solange keine Kräfte wirken, befindet man sich auf der Geodäte.

Effektiv ist es doch nur eine kurzer Zeit, in der du dich schwerelos fühlst. (Außer, du definierst diese kurze Zeit als den Parabelflug, den Rest nur als Flug, um hin- und wieder weg zu fliegen. Passt wahrscheinlich wirklich besser...)

mojorisin schrieb:Der Ball befindet sich aber im freien Fall solange er keine Kräfte spürt, d.h. sobald er die Hand verlässt und bevor er auf dem Boden aufkommt.

Hast recht, vor kurzem haben wir das schonmal durchgekaut. Ich denke bei so „trivialen“ Sachen wie dem Ball immer irgendwie eine Mischung aus Newton, in diesem Kontext nicht zu betrachtende Effekte wie bspw. der Luftwiderstand, und Relativitätstheorie, es geht jedesmal schief, und ich mache es trotzdem immer wieder... Bei Alltagserfahrungen ist das alles irgendwie schwerer einzusehen, als bei Schwarzen Löchern. Bei denen spielt die eigene Intuition nämlich keine Rolle... ;)

Zumindest ist der Scheitelpunkt der Punkt, an dem man das Äquivalenzprinzip (m.E.) am unmittelbarsten einsehen kann... Ich muss noch mal bei Martin schauen, er hat das selbst mal so erklärt.

PS.: Zumindest mit dem Parabelflug lag ich nicht ganz falsch. Damit wird gemeinhin das gesamte Flugmanöver bezeichnet... ;)

Siehe z.B. hier:

Parabelflug, Flugmanöver, bei dem in Flugzeugen kurzzeitig der Zustand der Schwerelosigkeit mit großer Annäherung oder sogar absolut erreicht werden kann. Das Prinzip des Parabelfluges besteht darin, das Flugzeug eine Vertikalkurve durchfliegen zu lassen, auf der sich im Idealfall Fliehkraft (Zentrifugalkraft) und Gravitationskraft (Gravitation) kompensieren, so daß für das Flugzeug und seine Insassen der Schweredruck aufgehoben wird. Im Nahbereich der Erdoberfläche kann diese Kurve als Wurfparabel (Wurf) dargestellt werden, obwohl sie eigentlich ein Ellipsenabschnitt ist.

https://www.spektrum.de/lexikon/physik/parabelflug/10868

@majorisin

Ah, hab's wieder gedanklich sortiert! :)

Der Scheitelpunkt ist kein besonderer Ort bzgl. des Falls entlang der Geodäte (noch mal danke für die erneute Korrektur!).

Aber es gibt dort einen im Bezug auf den Ball kräftefreien Beobachter, der ggü. dem Ball nicht beschleunigt ist und dessen Bezugssystem mit dem des Balls übereinstimmt. Von daher ist das schon ein ausgezeichneter Punkt, da die Koordinaten der beiden Bezuggsysteme übereinstimmen und das Bezugssystem des kräftefreie Beobachters ein Inertialsystem ist. D.h. hier ist die Raumzeit lokal flach, und das kann man unmittelbar einsehen.

Während der Ball die restliche Bahn entlang fällt, oder während er einfach nur auf der Erde herumliegt, gibt es einen solchen Beobachter nicht. Hier gibt es immer nur kräftefreie Beobachter, gegenüber denen der Ball beschleunigt ist. Auch für diese Bezugssysteme lässt sich ein passende Inertialsystem finden, in das die Koordinaten mittels Lorentztransformation überführt werden können. Also ist auch hier die Raumzeit lokal flach. Man kann es aber nicht mehr so unmittelbar einsehen...

(Das hatte ich ursprünglich auch so geschrieben, s. meinen Text zu diesem Thema weiter vorne. Aber dann leider wieder durcheinander gewirbelt...)

@mojorisin

Arrakai schrieb:Aber es gibt dort einen im Bezug auf den Ball kräftefreien Beobachter, der ggü. dem Ball nicht beschleunigt ist und dessen Bezugssystem mit dem des Balls übereinstimmt.

Stimmt, so war die Begründung am Anfang, da sehe ich dein Argument ;-).
Dennoch bin ich nicht überzeugt das es sehr hilfreich ist (oder gar einfach nicht stimmt). Und zwar deshalb:

Arrakai schrieb:D.h. hier ist die Raumzeit lokal flach, und das kann man unmittelbar einsehen.

Die lokale Raumzeit ist für den Freifaller immer flach, egal an welchem Punkt. Für den gerade richtig positionierten, entfernten Beobachter hingegen ist am Scheitelpunkt nur die Geschwindigkeit des Beobachtungsobjektes gleich null, nicht jedoch die Beschleunigung. Daher ist das nicht dasselbe, denn nicht die Geschwindigkeit ist maßgeblich sondern die Beschleunigung. Oder genauer: Für den exterenen Beobachter ist zwar die Relativgeschwindigkeit am Schweitelunkt null, nicht aber die Beschleunigung (und genau das ist der UNterschied). Die ist aus Sicht des entfernten Beobachters z.B. bei konstant 9,81 m/s² im annähernden Minkowski-Raum würde das nie der Fall sein.

Wenn nicht genau klar ist was ich meine kann ich auch später noch etwas genauer schreiben ;-)

mojorisin schrieb:Die lokale Raumzeit ist für den Freifaller immer flach, egal an welchem Punkt.

Okay, ja, aber das hatte ich doch geschrieben.

Scheitelpunkt:

Arrakai schrieb:D.h. hier ist die Raumzeit lokal flach, und das kann man unmittelbar einsehen.

Ãœberall anders:

Arrakai schrieb:Also ist auch hier die Raumzeit lokal flach.

Der einzige Unterschied ist, dass das Bezugssystem des Beobachters einmal relativ zum Ball nicht beschleunigt wird, das andere Mal aber schon.

mojorisin schrieb:Oder genauer: Für den exterenen Beobachter ist zwar die Relativgeschwindigkeit am Schweitelunkt null, nicht aber die Beschleunigung (und genau das ist der UNterschied).

Habe ich das nicht genauso geschrieben?

Arrakai schrieb:(...) Beobachter, der ggü. dem Ball nicht beschleunigt ist (...)
Beobachter, gegenüber denen der Ball beschleunigt ist. (...)

@Arrakai

Arrakai schrieb:Habe ich das nicht genauso geschrieben?

Ich habe mich eigentlich auf das bezogen:

Arrakai schrieb:Der Scheitelpunkt ist kein besonderer Ort bzgl. des Falls entlang der Geodäte (noch mal danke für die erneute Korrektur!).

Aber es gibt dort einen im Bezug auf den Ball kräftefreien Beobachter, der ggü. dem Ball nicht beschleunigt ist und dessen Bezugssystem mit dem des Balls übereinstimmt.

Und das stimmt dann nicht, denn der Ball ist gegenüber einem Minkowki-Beobachter überall beschleunigt auch am Scheitelpunkt.

Für den Ball in dessen Bezugssystem gibt es keinen Scheitelpunkt, also ist dessen Raumzeit auch nicht "an diesem Punkt flach". Den Scheitelpunkt kann nur ein Beobachter von einem anderen Bezugssystem aus wahrnehmen. Für den Ball und dessen Bezugssystem ist der Raum flach, und zwar zu jedem Zeitpunkt (in dem er kräftefrei "ruht").

Für den Beobachter, der einen Scheitelpunkt der Ball-Geodäte wahrnehmen kann, ist die Raumzeit auch am Scheitelpunkt der Ballbahn nicht flach.

perttivalkonen schrieb:Für den Ball in dessen Bezugssystem gibt es keinen Scheitelpunkt, also ist dessen Raumzeit auch nicht "an diesem Punkt flach". Den Scheitelpunkt kann nur ein Beobachter von einem anderen Bezugssystem aus wahrnehmen. Für den Ball und dessen Bezugssystem ist der Raum flach, und zwar zu jedem Zeitpunkt (in dem er kräftefrei "ruht").

Aber ich habe doch genau dasselbe geschrieben, oder?

Noch mal zusammengefasst:

Der kräftefreien Beobachter, der ggü. dem Ball nicht beschleunigt, nimmt den Scheitelpunkt wahr. Und da dieser sich in einem Inertialsystem befindet, muss der Ball sich aufgrund des Äquivalentprinzips am Scheitelpunkt ebenfalls in einer lokal flachen Raumzeit befinden (egal, ob der Ball diesen Scheitelpunkt wahrnehmen kann oder nicht).

Wenn der Ball sich nicht am Scheitelpunkt befindet, ist die Raumzeit aus seiner Sicht trotzdem lokal flach. Denn es gibt einen kräftefreien Beobachter, gegenüber dem der Ball zwar beschleunigt ist. Aber auch für dieses Bezugssysteme lässt sich eine passende Lorentztransformation finden, sodass auch hier die Raumzeit lokal flach sein muss.

Wo ist denn jetzt der Unterschied zwischen unseren Aussagen?

mojorisin schrieb:Und das stimmt dann nicht, denn der Ball ist gegenüber einem Minkowki-Beobachter überall beschleunigt auch am Scheitelpunkt.

Lass mich noch mal nachdenken, wie ich das erklären kann. Wenn mir nichts dazu einfällt, liege ich wahrscheinlich falsch... ;)

perttivalkonen schrieb:Für den Beobachter, der einen Scheitelpunkt der Ball-Geodäte wahrnehmen kann, ist die Raumzeit auch am Scheitelpunkt der Ballbahn nicht flach.

Ah, den Teil hatte ich ausgeblendet... Weshalb sollte das so sein?

Arrakai schrieb:Weshalb sollte das so sein?

Weil die Beschleunigung dort nicht null ist.

mojorisin schrieb:Weil die Beschleunigung dort nicht null ist.

Unter der Voraussetzung, dass deine Aussage

mojorisin schrieb:Und das stimmt dann nicht, denn der Ball ist gegenüber einem Minkowki-Beobachter überall beschleunigt auch am Scheitelpunkt.

korrekt ist. Da bin ich allerdings (noch) anderer Meinung. Da meine Aussage von Martin kommt, könnte es aber auch sein, dass du dich irrst... Bevor das nicht klar ist, solltest du m.E. zumindest diese Einschränkung bzgl. deiner Aussage machen...

Momentan habe ich leider nicht die Zeit, um das noch mal genauer zu durchdenken und für mich nachzuvollziehen. Die Aussage von Martin hatte ich einfach so übernommen, an sich ja eine vertrauenswürdige Quelle... Und sie erscheint mir auch nach wie vor schlüssig. Was natürlich nichts heißen muss. Ich hoffe auf heute Abend...

@Arrakai

Arrakai schrieb:Unter der Voraussetzung, dass deine Aussage

mojorisin schrieb:
Und das stimmt dann nicht, denn der Ball ist gegenüber einem Minkowki-Beobachter überall beschleunigt auch am Scheitelpunkt.

korrekt ist. Da bin ich allerdings (noch) anderer Meinung.

Das ist kein Problem ich bin da ergebnisoffen ;-) Es dauert manchmal nur bis ich überzeugt bin falsch zu liegen :-)

Dennoch kurze Zeichnung dazu:

Original anzeigen (0,3 MB)

Die drei Trajektorien (Weg-Zeit, Geschwindigkeit-Zeit und Beschleunigung-Zeit-Diagramme) zeigen den Ball wie ihn ein extenern Beobachter sieht. Ein externer Beobachter im flachen Raum sieht den Ball konstant beschleunigt (unterer Graph), daher kommt er nicht auf die Idee das die Raumzeitumgebung in der der Ball sich bedfindet auch nur irgendwie flach wäre. Auch nicht am SChweitelpunkt wo die Geschwindigkeit kurzzeitig null beträgt.

Ich war so frei, bei Martin nachzufragen... Martin schreibt:

Der Ball ist im freien Fall, kräftefrei, und relativ zu dir in Ruhe, das ist es, was zählt. Momentan sind beide Geodäten in der Raumzeit parallel. Die Beschleunigung wird erst relevant, wenn man über einen längeren Zeitabschnitt guckt, dann weicht die Geodäte des frei fallenden Balls von deiner ab.

mojorisin schrieb:daher kommt er nicht auf die Idee das die Raumzeitumgebung in der der Ball sich bedfindet auch nur irgendwie flach wäre

Mal unabhängig von Martins Aussage: Was spielt das für eine Rolle?

Das Äquivalentzprinzip gilt lokal für den Ball. Es ist doch egal, wie ein Beobachter den Ball wahrnimmt.

@Arrakai

Ich bin nicht so richtig überzeigt ;-) Ich sage dir aber auch warum. Es ist richt das am Scheitelpunkt die Geschwindigkeit zwischen fernem Beobachter und Ball = 0 ist (Also in einem Bezugssystem in dem auch die Erde ruht.) Die Beschleunigung ist trotzdem konstant ungleich null.

Ok aber das habe ich schon geschrieben. Was mir nicht gefällt an Martins Antwort (Falls er das über seinen Blog beantwortet hat schick mal bitte den Link):

Arrakai schrieb:Momentan sind beide Geodäten in der Raumzeit parallel. Die Beschleunigung wird erst relevant, wenn man über einen längeren Zeitabschnitt guckt, dann weicht die Geodäte des frei fallenden Balls von deiner ab.

Die Geodäte des Balles ändert sich ja nicht während des Fluges sondern hängt nur von der krümmenden Masse ab und der Abschussgeschwindigkeit. Danach ist die Geodäte vorgegeben. Jetzt geibt es einen Punkt an dem die Geodäte dieselbe "Richtung" hat wie in einem flachen Raum, aber die Krümmung ist nicht diesselbe.

Ganz einfaches Beispiel:



In dem Bild sieht man ein Analogon zum gekrümmten und zum flachen Raum. Es gibt beim gekrümmten Raum Orte, an denen der Richtungsvektor parallel ist zum Richtungsvektor im flachen Raum. DIe Krümmung aber ist an jeder Stelle des Kreises = 1/r und somit anders als an der Ebene denn dort ist die Krümmung an jeder Stell = 0.