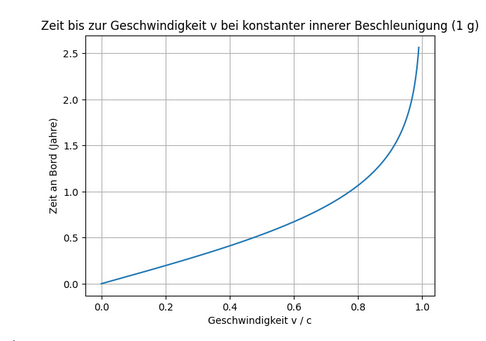
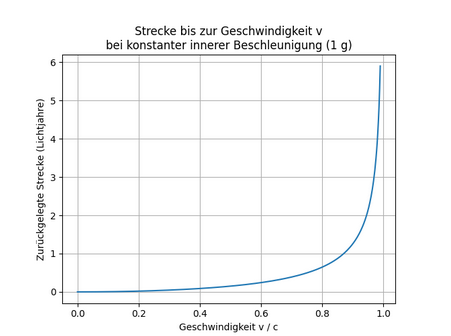
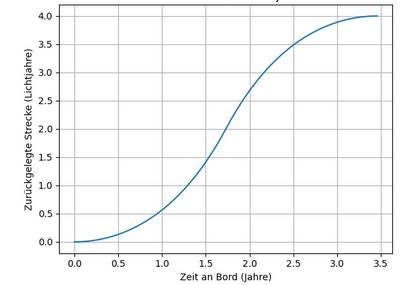
JosephConrad schrieb:
nocheinPoet schrieb:JosephConrad schrieb:nocheinPoet schrieb:Solche Dinge verwirren vermutlich mehr, also sie hier denen helfen, die da noch im Nebel stehen.
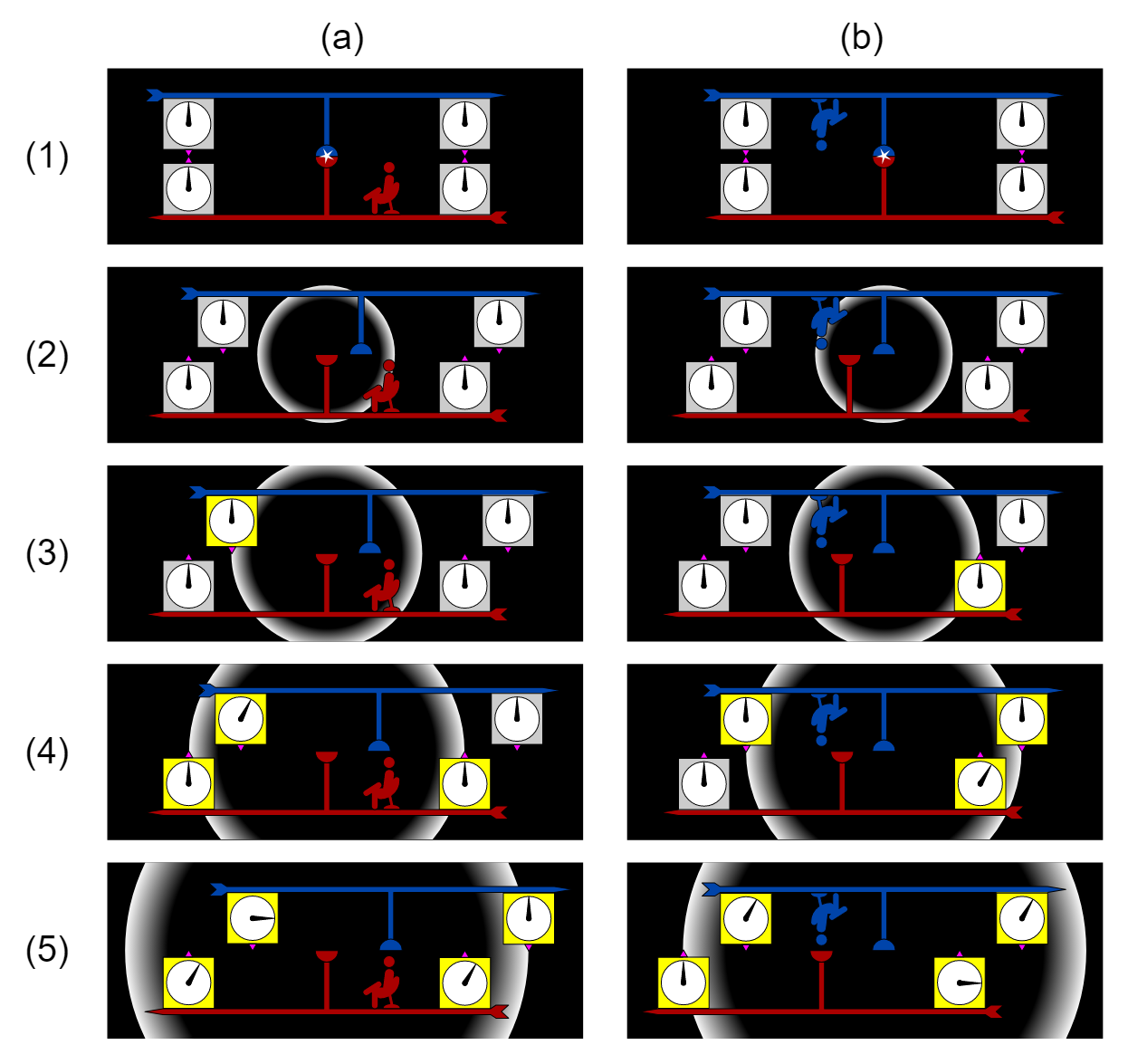
Weiss ich nicht, klingt doch einfacher als Deine Erklärungen, die man nur als naturwissenschaftlicher Akademiker versteht. Ich fliege frontal auf einen Stern zu, der wird vor mir immer größer und ich bin nach 1,2 Monaten dort ... . Da ich so schnell war, habe ich in meinem Zeitsystem die Entfernung scheinbar mit 10facher Lichtgeschwindigkeit zurückgelegt. Erst wenn ich dort angehalten habe stelle ich fest, dass alles um mich herum leider ein Jahr älter ist und ich meine Uhr neu stellen muss.
Darum ging es doch, oder? Also mehr "Erklärung" finde ich hier nicht von Dir. Aber erstmal das hier, als "Erklärung", weil Du so schnell warst, hast Du in Deinem "Zeitsystem" die Entfernung scheinbar mit 10facher Lichtgeschwindigkeit zurückgelegt. Klar, wenn das mal nicht alles erklärt, da bleiben zur SRT und der Zeitdilatation ja nun ganz sicher keine Fragen mehr offen.
Völlig richtig, ich habe zunächst nur beschrieben, aber eben auch die Unterschiede klar gemacht. Vielleicht war das ja schon trivial, aber ich denke allein diese Beschreibung ist für so manche ein guter Einstieg. Und Deine Ausführung sind alle mathematisch/physikalisch korrekt, daran habe ich keinen Zweifel.
Ja, wie auch immer, die Frage und das Szenenbild war eigentlich recht klar, wurde ja nun mehrfach beschrieben. Und auch ich kann mal irren, sollte aber schon soweit passen.
JosephConrad schrieb:Ich habe mir aber gerade nochmal deine Einstiegsposts hier durchgelesen und Du kommst mMn. schnell mit "erschlagenden" Informationen.
Ich beziehe mich auf Deinen Post: nocheinPoet schrieb am 12.12.2025:Gut, ich setzte mich noch mal ein wenig in die Nesseln. :D
Nein, und ich habe mir eben den Beitrag noch mal angesehen, ich fange ganz vorne an und gebe extra zwei Videos rein, die Grundlagen erklären.
JosephConrad schrieb:Ich bin kein Lehrer, hatte aber Physik Leistungskurs uns später im Vordiplom Physik als Nebenfach aber sei es drum.
Nette Info, beides ist aber auch nicht nötig, habe auch nur Physik auf der Realschule gehabt, der Rest ist von mir autodidaktisch gelernt.
JosephConrad schrieb:Vielleicht würde es helfen die Zeitdilatation ausführlicher herzuleiten?
ㅤ
Ach nun, was soll das, ich habe genau das getan, und nebenbei, meine Erklärung, ist genau das, was auch hier gefallen hat:
Jimtonic schrieb:Für mich die einfachste Erklärung ab 4:55 in dem Video, ohne Bewegung vergeht die Zeit mit Lichtgeschwindigkeit. Relativ dazu vergeht die Zeit in Bewegung entsprechend langsamer.
ㅤ
Bei mir ist das die Aussage:
nocheinPoet schrieb am 12.12.2025:... alles bewegt sich immer mit \color{#f0e0d0}\mathrm{c} durch die Raumzeit,
Und dann kann man bei 6:53 im Video, genau die Gleichung von mir sehen, es wird ganz einfach mit Pythagoras berechnet, denn man kann es da unten noch mit der einfachen euklidischen Metrik erklären.
Hier meine Erklärung zum Vergleichen:
nocheinPoet schrieb am 12.12.2025:Wer nun echt das mit der SRT und der Zeitdilatation richtig verstehen will, der sollte eventuell mit dem Vierervektor anfangen, der ist nämlich konstant.
Bedeutet:
alles bewegt sich immer mit \color{#f0e0d0}\mathrm{c} durch die Raumzeit,
konkret für sich durch die Zeit.
Jede Bewegung im Raum kippt nun diesen Vektor \color{#f0e0d0}\mathrm{c = 1} und wir haben es hier nur mit Pythagoras zu tun.
\color{#f0e0d0}\mathrm{c^2=a^2+b^2}
Die Vierergeschwindigkeit setzt sich aus der Geschwindigkeit durch die Zeit \color{#f0e0d0}\mathrm{t} und durch die durch den Raum \color{#f0e0d0}\mathrm{r} zusammen und geometrisch addiert soll das \color{#f0e0d0}\mathrm{1} sein, also normiert.
\color{#f0e0d0}\mathrm{1=v_t^2+v_r^2}
Kennen wir die Geschwindigkeit einer \color{#f0e0d0}\mathrm{v} Uhr die in \color{#f0e0d0}\mathrm{S'} ruht, in \color{#f0e0d0}\mathrm{S}, können wir \color{#f0e0d0}\mathrm{v_t} ausrechnen, also die Geschwindigkeit durch die Zeit, welche die für uns in \color{#f0e0d0}\mathrm{S} bewegte Uhr noch hat.
\color{#f0e0d0}\mathrm{v_t^2= 1 - v_r^2}
\color{#f0e0d0}\mathrm{v_t = \sqrt{1 - v_r^2}}
... nehmen wir mal ein konkretes Beispiel zum Rechnen, die Uhr B (ruhend in \color{#f0e0d0}\mathrm{S'}) bewegt sich in \color{#f0e0d0}\mathrm{S} mit \color{#f0e0d0}\mathrm{v_r=0,8\hspace{1px}c} dann haben wir:
\color{#f0e0d0}\mathrm{v_t = \sqrt{1 - 0,8^2} = ... = 0,6}
Bedeutet, wenn die Uhr ruhend in \color{#f0e0d0}\mathrm{S} \color{#f0e0d0}\mathrm{1 s} zählt, hat die in \color{#f0e0d0}\mathrm{S} bewegte Uhr \color{#f0e0d0}\mathrm{B} genau \color{#f0e0d0}\mathrm{0,6 s} gezählt.
So, zur Klarstellung, ich habe das Zitat auseinander gezogen und mit Trennlinien verstehen, weil es sonst im Zitat hier zu unübersichtlich ist. Es ist aber verlinkt und jeder kann es ja auch original nachlesen.
Im Video schreibt er die Gleichung:
\color{#f0e0d0}\mathrm{t = \sqrt{c^2 - v^2}}Meine zum Vergleich:
\color{#f0e0d0}\mathrm{v_t = \sqrt{1 - v_r^2}}Ich habe es hier noch einfacher gemacht, weil ich die Lichtgeschwindigkeit normiert habe:
\color{#f0e0d0}\mathrm{c = 1} Damit hab ich ein konkretes Beispiel erklärt und so einfach wie nur möglich vorgerechnet. Einfach mal im Kopf behalten, ich komme noch weiter unten darauf zurück.
JosephConrad schrieb:Die Lichtgeschwindigkeit ist für alle gleich, Die Naturgesetze sind für alle gleich (egal, ob man sich bewegt oder stillsteht),
Du beginnst richtig mit Lichtgeschwindigkeit und Naturgesetze sind für alle gleich. Das erklärt aber nichts genaues für jene, die keinen Hintergrund haben. Was ist die konkrete Bedeutung dieser Aussage, jeder wird Licht in seinem Ruhesystem immer mit konstant c der Lichtgeschwindigkeit messen. Und auch das wird für viele so einfach nicht reichen.
Darum mal so, wenn Peter in einer Rakete an Karl vorbeifliegt und den Scheinwerfer nach vorne hin an hat, dann misst Peter, wie sich das Licht aus dem Scheinwerfer mit Lichtgeschwindigkeit von ihm entfernt.
Und nun kommt das "seltsame", auch Karl misst die Geschwindigkeit des Lichts aus dem Scheinwerfer von Peter nur mit Lichtgeschwindigkeit.
Das ist elementar wichtig:
Wir kennen, dass sich Geschwindigkeiten addieren, Peter fliegt mit 100 km/h und wirft einen Ball in Flugrichtung mit 20 km/h, dann misst Karl den Ball mit 120 km/h. Weil die Geschwindigkeit von Peter sich auf die vom Ball addiert.
Bei Licht ist das anders, da addiert sich keine Geschwindigkeit auf.
Die Wirkung ist beachtlich, egal wie lange Peter auch beschleunigt, egal wie schnell er für Karl auch wird, das Licht aus seinem Scheinwerfer wird sich für ihn immer nur mit Lichtgeschwindigkeit entfernen.
Stellen wir uns das mal genauer vor, Karl wirft einen Ball mit 20 km/h und Peter rennt nun dem Ball nach, mit 15 km/h, wie Karl misst. Normal würden wir dann davon ausgehen, dass der Ball sich nun von Peter nur noch mit 5 km/h entfernt, weil er selbst rennt ja schon mit 15 km/h hinterher.
Das ist bei Licht anders, wenn das kein Ball sondern ein Photon ist, kann Peter rennen wie er will, er wird immer nur 20 km/h messen.
JosephConrad schrieb:Wir brauchen eine Art "Abstand" zwischen Ereignissen im Raum und in der Zeit, der für alle Beobachter gleich ist.
Nun weiter, Du sprichst von einer Art "Abstand" zwischen Ereignissen in Raum und Zeit, der für alle gleich sein soll. Wir sollten schon erklären, dass ein Ereignis ein Punkt in einem Koordinatensystem ist. Du setzt hier schon viel voraus und gehst viel weiter als ich.
Sagst aber:
JosephConrad schrieb:Vielleicht würde es helfen die Zeitdilatation ausführlicher herzuleiten?
Meine Herleitung kannst Du ja nachlesen, findest Du ja zu "akademisch" und zu kompliziert. So was aber auch, aber nun gut, schauen wir uns Deine ausführlichere Herleitung mal weiter an.
JosephConrad schrieb:In der klassischen Physik: Abstand = Wurzel (Δx² + Δy² + Δz²)
Ja, aber zu viel, man könnte ja mindestens z rauslassen. Und wer keine Ahnung hat, weiß mit "Δ" nichts anzufangen, ist ein Dreieck, nett und nun?
Also wie wollen den Abstand zuerst mal nur auf der x-Achse zwischen zwei Punkten
\color{#f0e0d0}\mathrm{P_1} und
\color{#f0e0d0}\mathrm{P_2} wissen.
Das sind die Koordinaten \color{#f0e0d0}\mathrm{x_1} und \color{#f0e0d0}\mathrm{x_2} und dann rechnet man:
\color{#f0e0d0}\mathrm{\Delta x = x_2 - x_1}Muss man für x, y und z machen, die Gleichung ist dann das:
\color{#f0e0d0}\mathrm{d = \sqrt {\Delta x^2 + \Delta y^2 + \Delta z^2} = \sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}} Das sind die Grundlagen und das ist "ausführlich" für jene, die davon gar keine Ahnung haben. Der Weg, den Du hier aber gehst, der ist sehr komplex und wohl auch "akademisch". Ich ergänze das nur und zeige, was da eigentlich für eine ausführliche Erklärung so fehlt, aber schauen wir mal weiter ...
JosephConrad schrieb:In der Relativität: Zeit gehört auch dazu, aber nicht einfach addieren wie x, y, z.
Grund:
Zeit verhält sich anders als Raum, Zeit trägt per Konvention negativ zum Abstand bei.
ds²= −c²dt² + dx² + dy² + dz²
ds² misst quasi "wie weit auseinander zwei Ereignisse im Raum und in der Zeit sind".
Man nennt diese Formel: Minkowski-Metrik
Das ist dann schon echt der Knaller, hier erschlägst Du jeden ohne Ahnung mit einer Gleichung und einer "Begründung", die nur Fragezeichen stehenlässt. Erstmal zum "Grund", Zeit verhält sich eben anders und einfach so "per Konvention" trägt sie nun negativ zum Abstand bei?
Ja, ist so, aber nicht per Konvention, ergibt sich so aus der Metrik der Raumzeit. Und dann diese Gleichung von Dir, erschlägt doch jeden. Dann hast Du hier kein Δx mehr drin, sondern schreibst nun dx. Warum bleibst Du nicht bei dem, was Du davor "erklärt" hast, oder sagen wir mal, gezeigt?
Ich mach mal eben was:
\color{#f0e0d0}\mathrm{ds^2 = -c^2dt^2 + dr^2} Wenn wir nun noch vorgeben, dass die Lichtgeschwindigkeit c = 1 ist, schaust es so aus:
\color{#f0e0d0}\mathrm{ds^2 = -dt^2 + dr^2} Besser, aber jeder der den Pythagoras kennt, fragt ganz sicher, ja was soll das Minuszeichen da vor dem
\color{#f0e0d0}\mathrm{dt^2}?
Und nun nur zu sagen, ja ist weil "Zeit trägt per Konvention negativ zum Abstand bei", wird nicht helfen.
Nehmen wir mal meine Gleichung (und die aus dem Video) nochmal zum Vergleich:
\color{#f0e0d0}\mathrm{v_t = \sqrt{1 - v_r^2}}Und ist doch schon was anderes, nebenbei, \color{#f0e0d0}\mathrm{v_t} ist der Kehrwert des Gammafaktors:
\color{#f0e0d0}\mathrm{\gamma = \frac {1}{v_t} = \frac {1}{\sqrt{1-v_r^2}} = v_t^{-1}}Nun könnte wer fragen, ja warum geht das hier denn nun so ohne das Minuszeichen?
Die Erklärung wäre,
\color{#f0e0d0}\mathrm{v_t} entspricht nicht der Koordinatenzeit-Komponente
\color{#f0e0d0}\mathrm{\gamma}, sondern der Ableitung der Eigenzeit nach der Koordinatenzeit, also
\color{#f0e0d0}\mathrm{\frac{\Delta \tau}{\Delta t} = 1}. Aber auch das will verstanden wissen und dafür müsste ich noch weiter ausholen. Und es ist ja so hier auch erstmal nicht nötig.
Aber mal weiter.
JosephConrad schrieb:ds² misst quasi "wie weit auseinander zwei Ereignisse im Raum und in der Zeit sind".
Man nennt diese Formel: Minkowski-Metrik
Nicht wirklich ganz, eine Formel ist nicht dasselbe wie ein mathematisches Objekt (Tensorfeld).
Streng genommen ist die Metrik das Tensorfeld
\color{#f0e0d0}\mathrm{\bm{g}}, und
\color{#f0e0d0}\mathrm{\Delta s^2} ist das Linienelement, das aus der Metrik und Koordinatendifferenzialen gebildet wird. Aber lassen wir das einfach mal unter den Tisch fallen, ich weiß, es kommt vor, dass die Formel auch mal Metrik genannt wird, auch wenn es nicht ganz richtig ist.
Man kann sagen mit einer durch das Linienelement
\color{#f0e0d0}\mathrm{ds^2 = c^2 dt^2 - (dx^2 + dy^2 + dz^2)} definierten Metrik, wäre das ein flacher Raum, der nicht gekrümmt ist, also ohne Gravitation. Und in so einem Minkowski-Raum, also mit der Minkowski-Metrik, lässt sich die Spezielle Relativitätstheorie (SRT) dann recht einfach auch grafisch darstellen.
Und nun sagst Du, ds² misst "quasi" wie weit auseinander zwei Ereignisse im Raum und in der Zeit sind. Das ist schon schwierig, weil normal kennt man ja den Pythagoras und da zieht man dann noch die Wurzel.
Somit ist der Term
\color{#f0e0d0}\mathrm{ds^2} schwer richtig zu greifen, also wenn man das erklären will.
\color{#f0e0d0}\mathrm{\sqrt {-ds^2}} Eigenzeit
\color{#f0e0d0}\mathrm{\tau} \color{#f0e0d0}\mathrm{\sqrt {+ds^2}} Raumartiger Abstand
\color{#f0e0d0}\mathrm{\sigma} Gut, bis hier hast Du nichts vorgerechnet, wir schauen mal weiter.
JosephConrad schrieb:Annahme: es gibt zwei Ereignisse: A: "Start", B: "Ankunft" dann sagt ds² nicht, wie man von A nach B kommt, sondern was für eine Art Trennung A und B haben. Es misst nicht einen Weg, sondern die Struktur der Raum-Zeit selbst.
Ich glaube nicht, dass nun wer hier was damit anfangen kann, wenn Du sagst, es misst die Struktur der Raumzeit selbst. Wie wird die Struktur gemessen? Hä?
;)Erstmal macht es Sinn, zu erklären, ein Ereignis ist nur ein Punkt in einem Koordinatensystem. Zwischen zwei Punkten gibt es einen Abstand, ein Koordinatensystem sollte schon zwei Achsen haben. Den Abstand zwischen zwei solcher Punkte, von mir aus auch A und B habe ich oben über den Pythagoras berechnet. Hier reicht erstmal wirklich die euklidische Metrik aus.
\color{#f0e0d0}\mathrm{v_t = \sqrt{1 - v_r^2}}Du wirst hier so schnell keinem eben mal die Minkowski-Metrik erklären können, da wird wohl fast jeder aussteigen, und wer nicht aussteigt kennt die eh und weiß wohl auch, was die Zeitdilatation ist. Darum so einfach es eben geht, einfach bei der euklidischen Metrik bleiben, so wie der das da am Anfang im Video zeigt.
JosephConrad schrieb:Es sagt nicht: "Wie weit ist etwas geflogen?" sondern: "Welche Art von Verbindung ist zwischen zwei Ereignissen möglich?" ds² wird für jedes beliebige Paar von Ereignissen berechnet Auch wenn: kein Licht ausgesendet wurde, kein Teilchen existiert, niemand etwas gemessen hat. Es ist eine Eigenschaft der Raum-Zeit selbst, nicht eines Objekts.
Oh man, es erklärt nichts, ich mag das erstmal nicht auch noch aufarbeiten, eventuell schieb ich das noch einmal nach.
JosephConrad schrieb:Das Vorzeichen von ds² sagt aus:
< 0 zeitartig → langsames Objekt möglich
= 0 lichtartig → nur Licht
> 0 raumartig → keine Verbindung möglich
Ja, aber bitte, es geht um die Zeitdilatation, dass ist SRT, wer soll hier an der Stelle nun damit etwas anfangen können?
Wollte ich das richtig erklären, würde ich einen eigenen Beitrag aufmachen, ich werde das hier auch nicht jetzt erklären, der Beitrag ist ja so schon wieder ein Roman geworden. Weißt Du, ich habe den Eindruck, Du hast Dir da nun hier und da und dort was aus dem Netz gesucht, und alles mal in einen Topf geworfen und durchgerührt, es fällt mir sehr schwer zu glauben, dass Du das alles so selbst verstanden hast. Bei Deiner Erklärung fehlt der Faden, ein Aufbau, eine Struktur. Komme ich gleich noch mal drauf zurück.
JosephConrad schrieb:Das Vorzeichen von ds² sagt aus:
Warum steht da überall ein d vor den Variablen?
dx – "infinitesimal klein"
dx ist ein extrem kleiner Schritt, praktisch unendlich klein.
Man denkt an den Grenzwert, wenn Δx → 0
Beispiel:
Stell dir vor, du gehst die Strecke von 2 m bis 5 m in unendlich kleine Schritte:
dx1, dx2, dx3,… Summe aller dxi ergibt 3 m.
Kann doch nicht Dein Ernst sein, das Δ und das d hättest Du mal ganz oben am Anfang erklären sollen, eventuell einfach über "d" für Differenz? Wer kann hier was mit "Grenzwert" anfangen, geht doch um Zeitdilatation?
JosephConrad schrieb:Warum das wichtig ist:
In der Physik wollen wir kontinuierliche Bewegungen oder Abstände berechnen. Die Minkowski-Metrik benutzt dx, dy, dz, dt weil wir den infinitesimalen Raum-Zeit-Abstand ds zwischen zwei Ereignissen definieren: ...
Ja wie nun? Das is wichtig, weil wir in der Physik kontinuierliche Bewegungen oder Abstände berechnen wollen? Und ds ist nun der infinitesimalen Raumzeitabstand?
Dir ist doch aber klar, dass Du vorhin geschrieben hast:
JosephConrad schrieb:Das Vorzeichen von ds² sagt aus: < 0 zeitartig → langsames Objekt möglich.
Nun schreibst Du hier ds und benennst das als infinitesimalen Raumzeitabstand, aber du hast schon (richtig) geschrieben, dass ds² < 0 sein kann, dann ist der negativ. Dann ist √ (ds²) bei (ds < 0) schon etwas imaginär oder?
Wie willst Du nun ds und ds² denn verstanden wissen und wie untereinander abgrenzen?
JosephConrad schrieb:Später kann man ds ds über Integrale summieren, um größere Abstände zu finden: s =∫ds
Also ds ds und nun noch eben mal über Integrale summieren, klar, kann jeder hier, alle die nach der Zeitdilatation fragen, summieren locker so über Integrale.
;)
JosephConrad schrieb:Interpretation von ds²:
ds² hat zu tun mit der "Eigenzeit": Eigenzeit (τ) ist: die Zeit, die eine Uhr selbst misst, wenn sie sich mit dem Objekt mit bewegt.
Ja hat schon was damit zu tun, und auch mit dem räumlichen Abstand, etwas hiervon und davon, und ja, die Eigenzeit ist die Zeit, welche eine Uhr selbst misst, also die Differenz, wenn man dieselbe Uhr zweimal abliest.
JosephConrad schrieb:Beispiele:
Uhr im Raumschiff
Uhr an deinem Handgelenk
Uhr eines Teilchens
Nicht die Zeit eines außenstehenden Beobachters.
Man definiert:
ds² = -c²dτ² also dτ = (1/c) Wurzel (-ds²)
Nun hast Du so viel geschrieben und so "ausführlich" was erklärt, und nun definierst Du einfach nur so was? Also warum ist das nun so, was hat das mit der Zeitdilatation zu tun, wie erklärt sich hier nun genau was?
JosephConrad schrieb:Dadurch, dass da -ds² steht wird bei negativem ds² das ganze positiv und man kann die Wurzel ziehen.
Ja, aber warum, warum kann ds² überhaupt negativ sein, und haben sich die Physiker da gedacht, ja ist doch Mist, imaginäre Eigenzeit ist doof, also schreiben mir mal ein Minus davor, damit dass dann wieder positiv wird, läuft ...
:D
JosephConrad schrieb:Für ein Teilchen mit der Geschwindigkeit v gilt v²dt² = (dx² + dy² + dz²)
Warum gilt das so? Warum nun v²dt²? Und was ist mit c?
JosephConrad schrieb:Einsetzen in die Mintrowski [sic!]-Metrik:
ds² = −c²dt² + v²dt² = −c²dt² (1 − v²/c²)
und weil ds²= −c² dτ² (s.o.)
dτ = dt Wurzel (1−v²/c²)
Das ist exakt die Zeitdilatation!
So, so, damit ist dann ja alles ganz sicher für jeden hier nun wirklich geklärt.
:DIch hatte ja nun
\color{#f0e0d0}\mathrm{v_t = \sqrt{1 - v_r^2}} abgeleitet, kannst ja mein Zitat oben nachlesen, ist doch recht kurz und einfach, im Vergleich zu Deiner ausführlichen Erklärung der Zeitdilatation.
JosephConrad schrieb:Physikalische Bedeutung:
ds ist der invariante Raum-Zeit-Abstand Für materielle Objekte (ds² < 0): ds misst direkt die Eigenzeit. Die Eigenzeit ist: für alle Beobachter gleich, messbar mit einer Uhr, unabhängig vom Koordinatensystem.
Das ist ja nicht falsch, aber es hilft hier doch keinem weiter, ich gehe auch schwer davon aus, dass Du vieles hier von dem, was Du geschrieben hast, nicht selbst wirklich verstehst und nachvollzogen hast.
So, mal deutlich und ehrlich Worte:
Mir gefällt Dein Beitrag!
Echt jetzt, hast Du nicht mit gerechnet was? Und wirklich, meine Anerkennung, Du hast Dir Zeit genommen, hier versucht etwas zu erklären, was nicht trivial ist, das ist doch schon wirklich was, machen hier inzwischen nur noch wenig User. Also alleine das verdient ehrliche Anerkennung, sehr gut.
Und weil ich das anerkenne, hab ich Dir nun so eine lange Antwort geschrieben, nicht um Dich lächerlich zu machen, nicht um Deinen Beitrag zu zerfetzten, nein, dass ist ganz aufrichtig und ehrlich konstruktive Kritik. Keine Erklärung ist perfekt, und auch ich mache Fehler und auch ich schreibe mal zu viel, oder zu wenig.
Du hast Dir ja echt Mühe gegeben, dass wo überall zusammengesucht, also ich gehe mal davon aus, Du hast nicht nur eine Quelle genutzt, die könnte man noch angeben, und ich gehe davon aus, dass Dein Werk auch Dein Werk ist, und so nicht von einer KI geschrieben wurde. Weil eine KI versteht den Hintergrund, das hier wirkt mehr wie ein Puzzle, wo Du Dir aber echt doch Mühe gegeben hast.
Eventuell erkennst Du nun aber - denk mal drüber nach
;) - wie aufwändig solche Erklärungen sind, und wie schwierig es ist, dass wirklich richtig und einfach zu erklären.
