nocheinPoet
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
anwesend
dabei seit 2006
dabei seit 2006
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Eine Frage zu Einstein und seiner Relativitätstheorie
12.12.2025 um 18:57Gut, ich setzte mich noch mal ein wenig in die Nesseln. :D
So, das ist wirklich elementar, das muss verstanden werden, wer Newton und die GT nicht versteht, wir Einstein und die Lorentz-Transformation (LT) nie verstehen können.
Wenn das hier verstanden ist, geht es damit weiter, dass wir bei der GT nur Raumkoordinaten unterschiedlich haben, bei der LT sind es aber auch Zeitkoordinaten die sich verändern, die Bewegung durch die Zeit ist nicht absolut. Dazu kommt, die Metrik, wir haben mit der Raumzeit keine euklidische Metrik, sondern die Minkowski-Metrik.
Wer nun echt das mit der SRT und der Zeitdilatation richtig verstehen will, der sollte eventuell mit dem Vierervektor anfangen, der ist nämlich konstant, bedeutet, alles bewegt sich immer mit c durch die Raumzeit, konkret für sich durch die Zeit. Jede Bewegung im Raum kippt nun diesen Vektor c = 1 und wir haben es hier nur mit Pythagoras zu tun.
c^2=a^2+b^2
Die Vierergeschwindigkeit setzt sich aus der Geschwindigkeit durch die Zeit t und durch die durch den Raum r zusammen und geometrisch addiert soll das 1 sein. Also normiert.
1=v_t^2+v_r^2
Kennen wir die Geschwindigkeit einer v Uhr die in S' ruht, in S, können wir v_t ausrechnen, also die Geschwindigkeit durch die Zeit, welche die für uns in S bewegte Uhr noch hat.
v_t^2 = 1 - v_r^2
v_t = \sqrt{1 - v_r^2}
Gut, nehmen wir mal ein konkretes Beispiel zum Rechnen, die Uhr B (ruhend in S') bewegt sich in S mit v_r = 0,8 c dann haben wir:
v_t = \sqrt{1 - 0,8^2} = \sqrt{1 - 0,64} = \sqrt{0,36} = 0,6
Bedeutet, wenn die Uhr ruhend in S 1 s zählt, hat die in S bewegte Uhr B genau 0,6 s gezählt.
Was ich eben gemacht habe, ist den Lorentzfaktor \gamma selbst abgeleitet, aus der Annahme, dass sich alles mit v = c = 1 durch die Raumzeit bewegt. Konkret hab ich den Kehrwert von \gamma abgeleitet, damit es zur SRT passt gilt nun:
\gamma = \frac{1}{v_t} = \frac{1}{0,6} = 1,\bar{6}
Und das gilt so auch für die Uhr A im System S', da die dort bewegt ist.
Ich will hier nun erstmal nicht weiter die SRT vortragen, nur mal kurz einen Einstieg zeigen, gut erklärt wird das mit der Vierergeschwindigkeit auch hier:
Das ist auch die Überlegung, die ich damals mit 15 Jahren hatte um mir das selbst abzuleiten, für eine Simulation am VC20. Andere Geschichte, ...
Eventuell erkläre ich das hier noch mal später mit einer anderen Analogie.
Und damit klar ist, dass ich nicht nur schwurble, zwei Grafiken die ich mal erstellt habe, um das zu erklären:
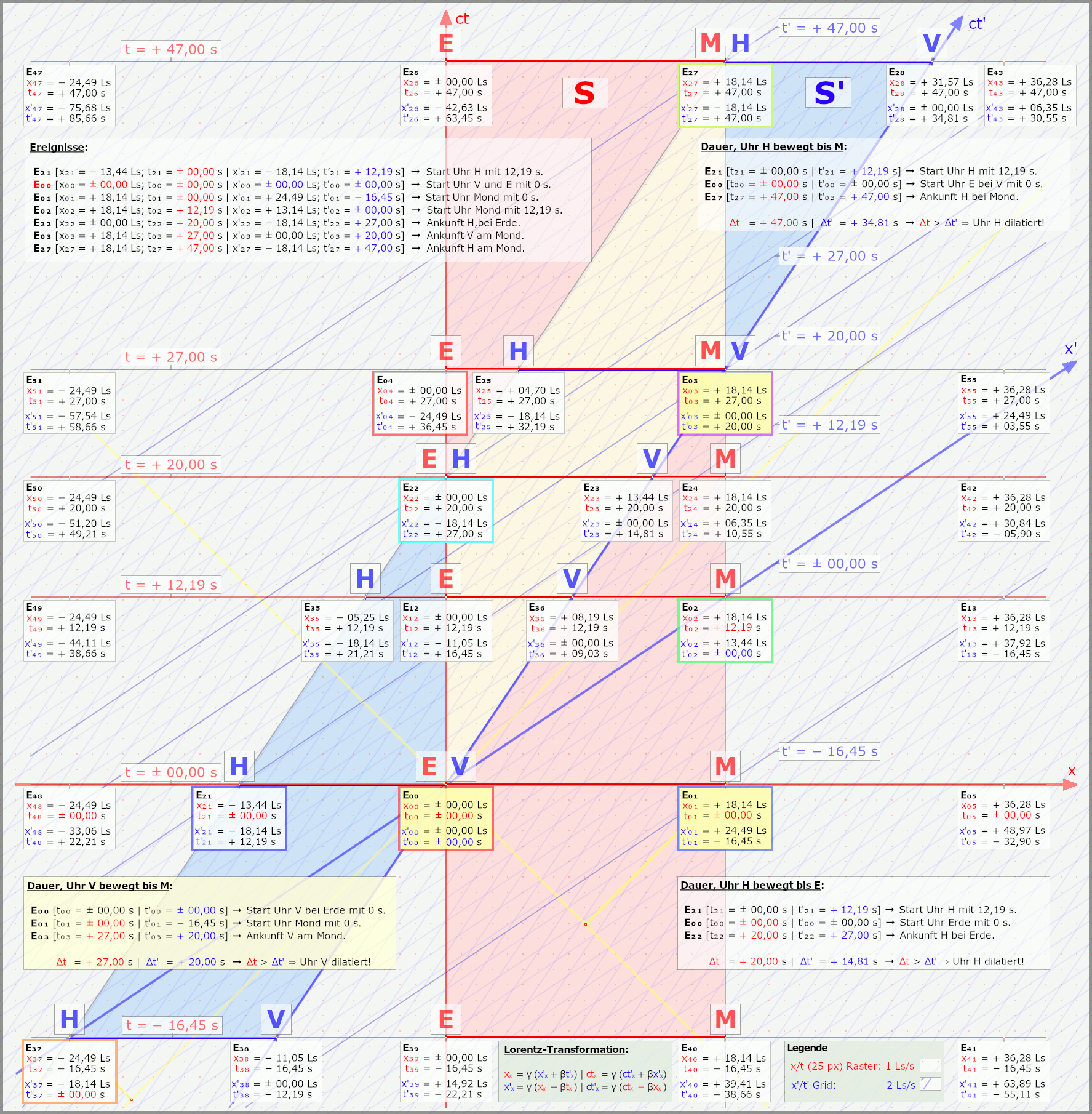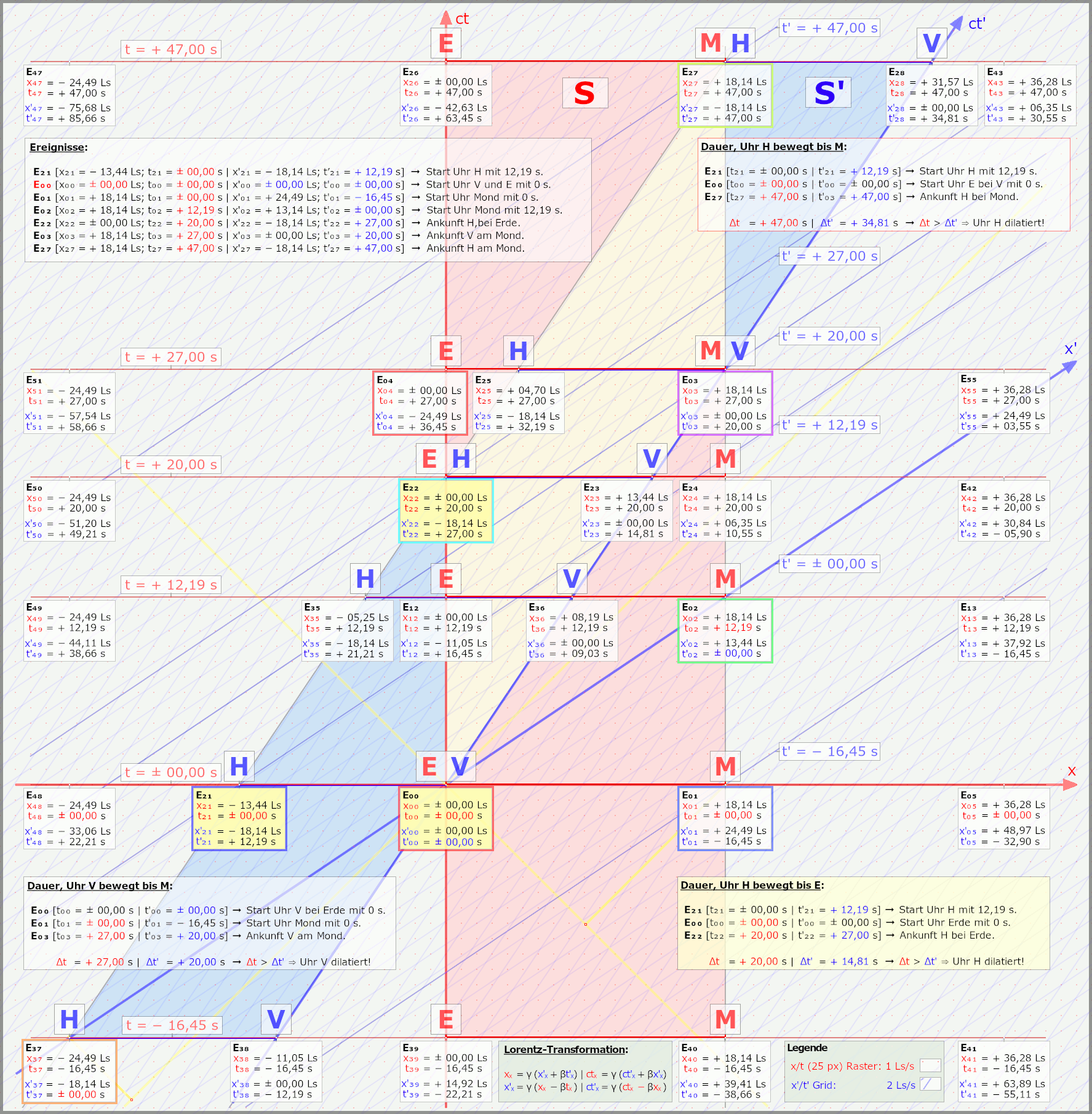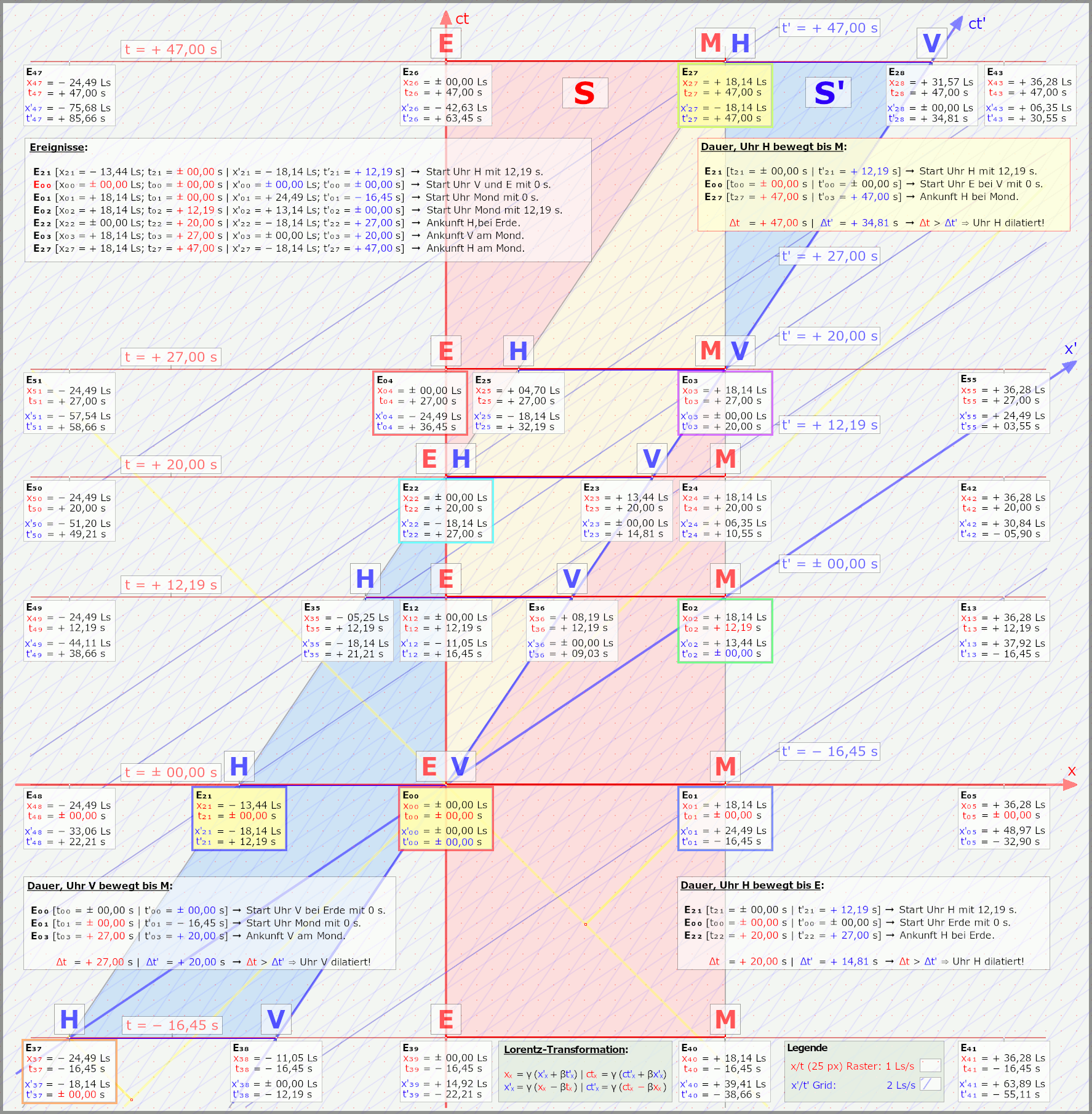
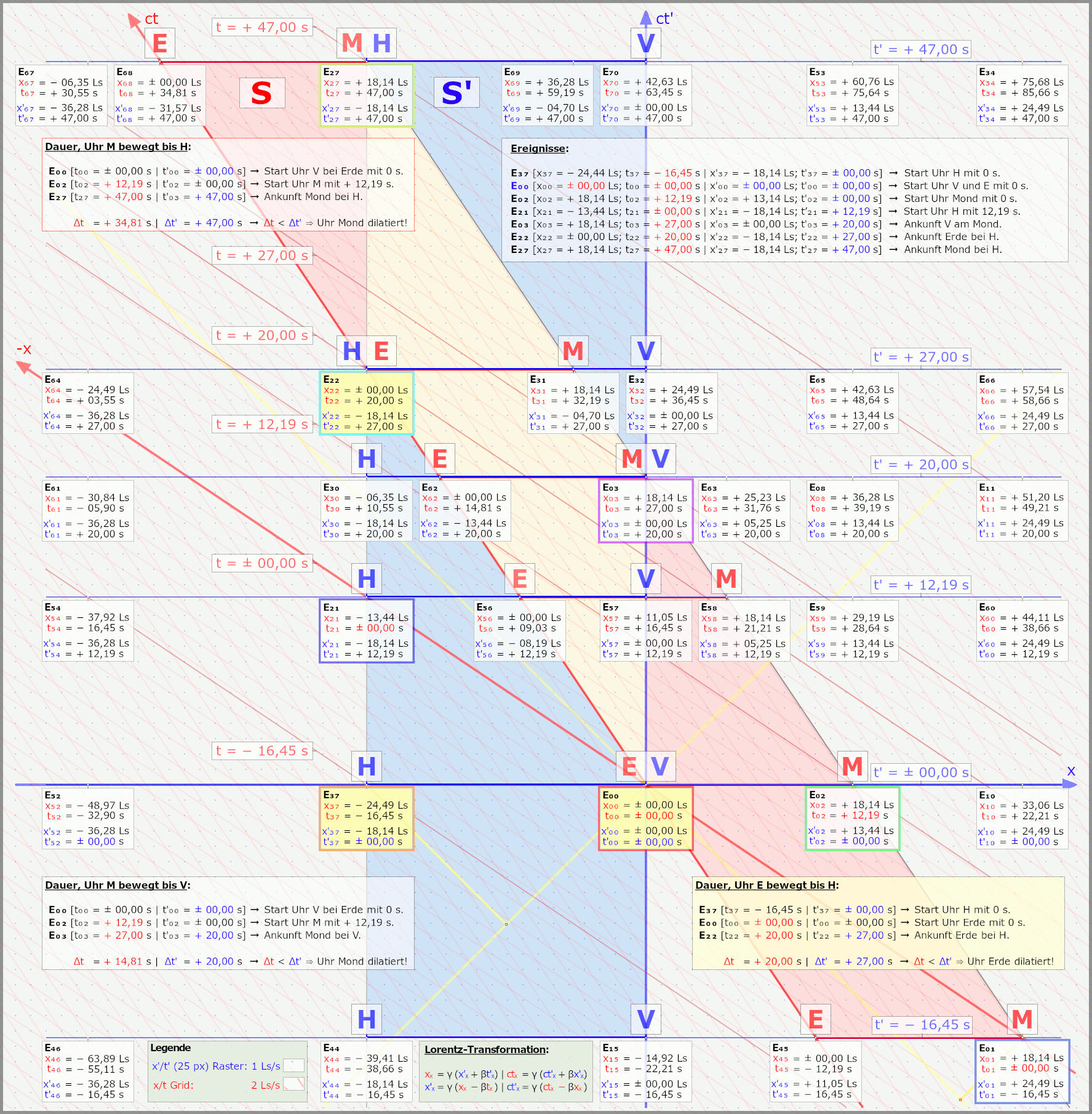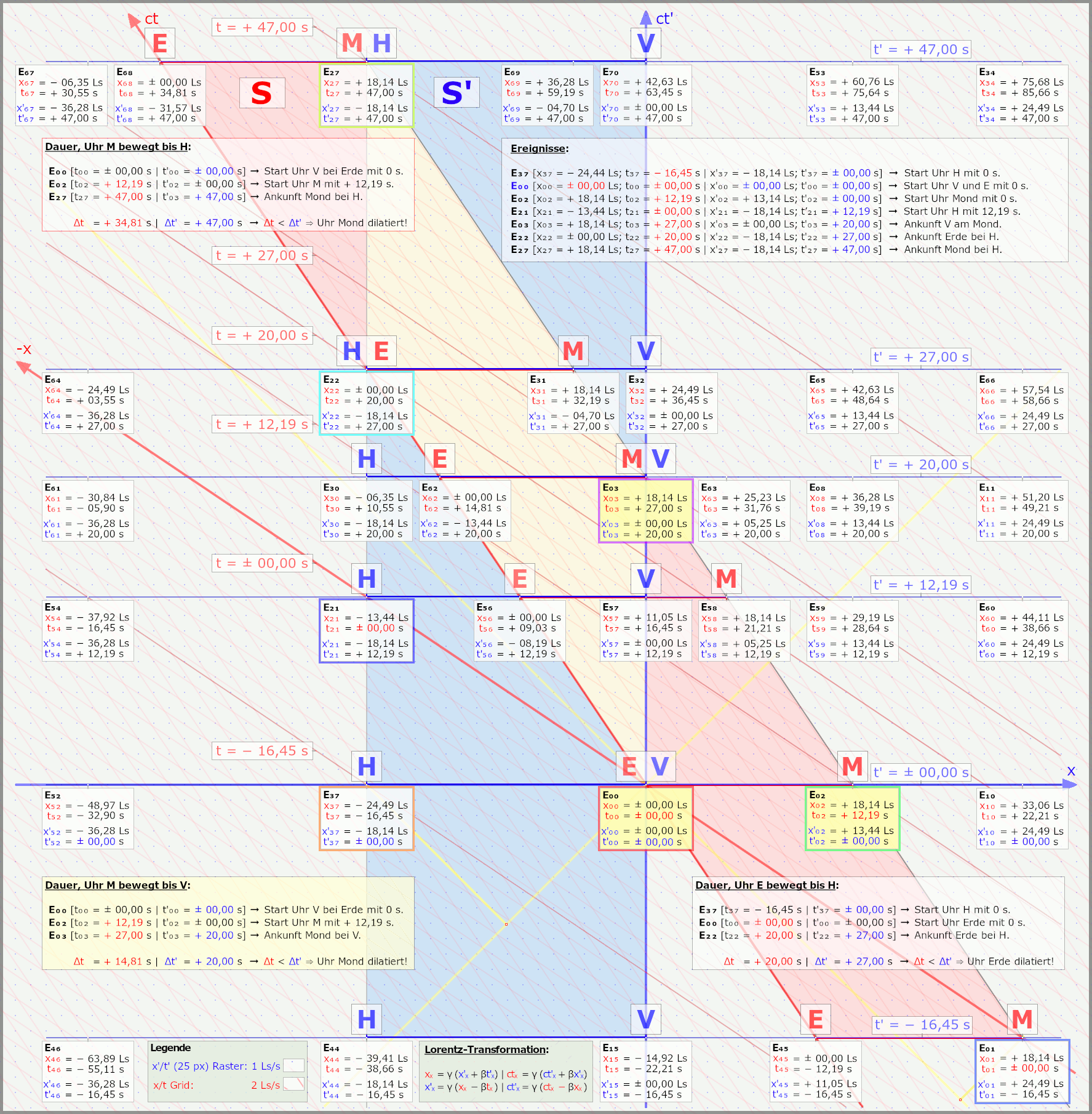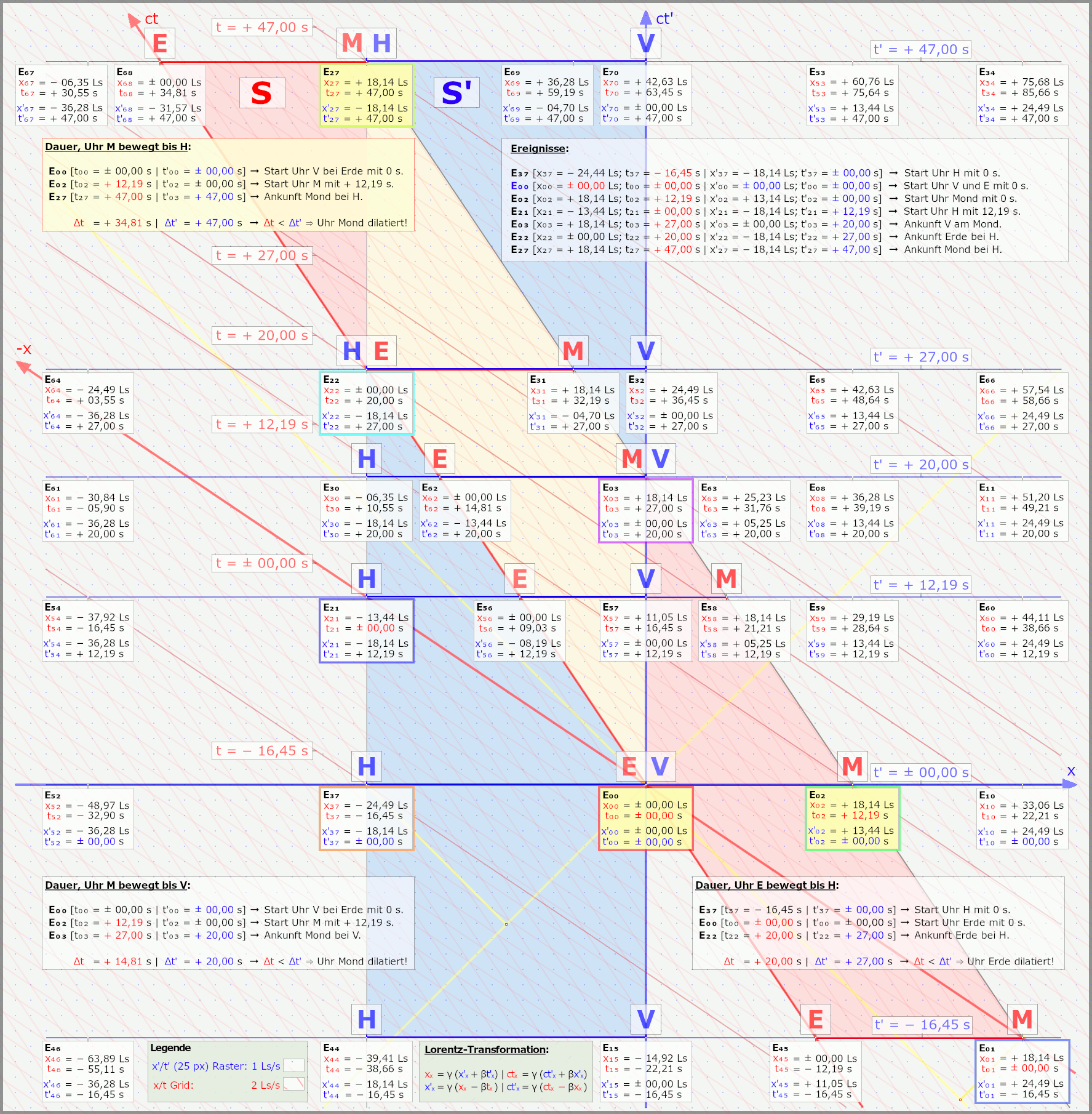
Ja, schaut ganz wild aus, will ich jetzt mal eben auch nicht erklären, nur damit klar ist, dass ich hier Euch nicht was vom Pferd erzähle. Und nur ganz kurz, die Grafiken zeigen aus zwei Systemen, wie zwei Raumschiffe aneinander vorbeifliegen, oder anders, ein Raumschiff (solang wie der Abstand Erde/Mond) fliegt an Erde/Mond vorbei. Im Grunde haben wir einfach zwei gleichlange Abstände, zwei "Stäbe" die vorne und hinten je eine Uhr haben, die treffen sich, bei E0 also dem Ereignis V/E und dann geht es eben so lustig weiter. Nebenbei sind es auch Animationen, steckt schon einiges an Arbeit drin.
Egal, wird Euch so erstmal kaum helfen, wenn die Grundlagen nicht klar sind, ansonsten sind da alle Rechnungen und Werte drin.
Damit es einfacher ist, setzt man hier in beiden Systemen S und S' den Nullpunkt, also x, t, x', t' = 0. Bedeutet, da ist eben 0 und beide Uhren dort zeigen 0 an. Man sollte bedenken, die Uhren sind nur Messgeräte, die auch virtuell sein könnten, es geht hier einfach um die Koordinatenwerte in S und S' für ein Ereignis, ein Punkt in der Raumzeit.
Nun kann man sich ein anderen Punkt in der Raumzeit anschauen, in den beiden Minkowski-Diagrammen ist das zum Beispiel E3, Raumschiff Vorne trifft den Mond (die Abstände sind nicht von mir, ein geistig nicht ganz so Bedachter, hat die mal vorgegeben, ich habe es dann nur dargestellt) die Uhr auf dem Mond zeigt nun 27 s an, die im Raumschiff nur 20 s.
Kurze Erklärung, erste Grafik zeigt das aus Sicht Erde/Mond, hier ist das Raumschiff bewegt, zweite Grafik zeigt das aus der Sicht des Astronauten im Raumschiff, hier sind Erde/Mond bewegt.
Der auf dem Mond kann nun sagen, ja die Uhr im Raumschiff ging doch langsamer, sie hat nur 20 s gezählt, meine aber 27 s, also q.e.d. und aus die Maus.
Nein, der im Raumschiff sieht es anders, der sagt nun, ja wir sind uns über die Anzeigen der Uhren bei E0 und E3 einig, beim Treffen am Mond zeigt die Uhr vorne im Raumschiff wirklich 20 s an und die auf dem Mond zeigt auch 27 s an.
Aber, und das ist ein ganz großes aber, also die Uhr von der Erde sich mit der Uhr vorne im Raumschiff bei E0 getroffen hat, hat die Uhr auf dem Mond für mich in S' nicht 0 s angezeigt, sondern sie zeigte schon 12,19 s.
Für mich in S' ist die Gleichzeitigkeit anders, Du auf dem Mond oder auf der Erde sagst, ja die Ereignisse E0 und E1 sind gleichzeitig, für mich sind die Ereignisse E0 und E2 gleichzeitig, die Uhr auf dem Mond zeigte eben schon etwas an. Und nun sind genau 14,81 s vergangen, für den "Flug" des Mondes zu meinem Raumschiff vorne.
Wäre ja auch logisch, weil der Abstand Erde/Mond von 18,14 Ls durch die Lorentzkontraktion bei mir eben nur 13,44 Ls sind.
Der Lorentzfaktor ist für beide gleich, jeder "misst" die Uhr des anderen langsamer laufend, scherzhaft umgangssprachlich mal formuliert. Ganz deutlich, wir haben es immer mit Differenzen zu tun, einem Delta Δ einen Abstand, die Differenz zwischen zwei Koordinatenwerten in einem System, zwei Punkte, zwei Ereignisse. also eben Δt = t2 - t1 oder so.
Um das hier zu verstehen, muss man wirklich die RdG verstehen, die Relativität der Gleichzeitigkeit, die Zeitdilatation bei Bewegung ist relativ und ergibst sich so nur aus der RdG. Das wird erst anders, wenn die Rakete umdreht und zurückfliegt, aber bis man dahin kommt, muss das hier verstanden sein und das ist schon ein kleiner Weg.
Egal, ich kann das alles gerne erklären, aber nicht nur, wer es verstehen will, muss hier auch selbst etwas machen und zwar die Grundlagen lernen, was ist ein Inertialsystem, ein Koordinatensystem, ein Punkt, ein Ereignis, was sind Abstände und wie berechnet man die richtig. Die beiden Grafiken sind für jene die das kennen und die Grundlagen verstehen recht einfach, für Euch vermutlich ein Topf Spagetti. :D
Du magst was richtiges meinen, die Aussage so ist aber falsch. Erstmal ist Bewegung relativ, da wirkt mal gar nichts und auch nicht auf die Zeit. Ist so, ich hoffe ich muss das nicht vorrechnen. :D Ich erkläre es weiter unten aber mal an einem Beispiel und nenne noch Quellen.Lupo54 schrieb:Es ist die Bewegung, die auf die Zeit wirkt. Und zwar unumkehrbar.
Das kann so nie was werden, geben wir doch einfach mal richtig, so wie bei Newton schon üblich, zwei Inertialsystem vor, S und S', beide sind zueinander bewegt. In S und in S' ruht eine Uhr oder auch beliebig viele. Und wir können zwischen beiden Systemen die Koordinaten transformieren, das schaut man sich zuerst mal bei Newton an mit der Galilei-Transformation (GT).
Zwei Uhren, eine unbewegt und eine bewegt die jetzt nebeneinander liegen laufen natürlich gleichschnell.
Galilei-Transformationen EINFACH erklärt! (Physik)
Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.
Beispielrechnung - Galilei-Transformationen, bewegte Bezugssysteme (Physik)
Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.
So, das ist wirklich elementar, das muss verstanden werden, wer Newton und die GT nicht versteht, wir Einstein und die Lorentz-Transformation (LT) nie verstehen können.
Wenn das hier verstanden ist, geht es damit weiter, dass wir bei der GT nur Raumkoordinaten unterschiedlich haben, bei der LT sind es aber auch Zeitkoordinaten die sich verändern, die Bewegung durch die Zeit ist nicht absolut. Dazu kommt, die Metrik, wir haben mit der Raumzeit keine euklidische Metrik, sondern die Minkowski-Metrik.
Minkowski-Diagramme EINFACH erklärt - Raum-Zeit-Diagramme, Gleichzeitigkeit (Physik)
Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.
Wer nun echt das mit der SRT und der Zeitdilatation richtig verstehen will, der sollte eventuell mit dem Vierervektor anfangen, der ist nämlich konstant, bedeutet, alles bewegt sich immer mit c durch die Raumzeit, konkret für sich durch die Zeit. Jede Bewegung im Raum kippt nun diesen Vektor c = 1 und wir haben es hier nur mit Pythagoras zu tun.
c^2=a^2+b^2
Die Vierergeschwindigkeit setzt sich aus der Geschwindigkeit durch die Zeit t und durch die durch den Raum r zusammen und geometrisch addiert soll das 1 sein. Also normiert.
1=v_t^2+v_r^2
Kennen wir die Geschwindigkeit einer v Uhr die in S' ruht, in S, können wir v_t ausrechnen, also die Geschwindigkeit durch die Zeit, welche die für uns in S bewegte Uhr noch hat.
v_t^2 = 1 - v_r^2
v_t = \sqrt{1 - v_r^2}
Gut, nehmen wir mal ein konkretes Beispiel zum Rechnen, die Uhr B (ruhend in S') bewegt sich in S mit v_r = 0,8 c dann haben wir:
v_t = \sqrt{1 - 0,8^2} = \sqrt{1 - 0,64} = \sqrt{0,36} = 0,6
Bedeutet, wenn die Uhr ruhend in S 1 s zählt, hat die in S bewegte Uhr B genau 0,6 s gezählt.
Was ich eben gemacht habe, ist den Lorentzfaktor \gamma selbst abgeleitet, aus der Annahme, dass sich alles mit v = c = 1 durch die Raumzeit bewegt. Konkret hab ich den Kehrwert von \gamma abgeleitet, damit es zur SRT passt gilt nun:
\gamma = \frac{1}{v_t} = \frac{1}{0,6} = 1,\bar{6}
Und das gilt so auch für die Uhr A im System S', da die dort bewegt ist.
Ich will hier nun erstmal nicht weiter die SRT vortragen, nur mal kurz einen Einstieg zeigen, gut erklärt wird das mit der Vierergeschwindigkeit auch hier:
Warum Sie sich nicht schneller als das Licht fortbewegen können liegt daran, dass Sie dies auch nicht langsamer als das Licht tun können. Es gibt nur eine Geschwindigkeit. Alles, wir mit eingeschlossen, bewegt sich stets mit Lichtgeschwindigkeit. Wieso können Sie sich bewegen, wo Sie doch auf einem Stuhl sitzen ? Sie bewegen sich durch die Zeit."Quelle: https://www.relativity.li/de/epstein/lesen/c0_de/c1_de
Das ist auch die Überlegung, die ich damals mit 15 Jahren hatte um mir das selbst abzuleiten, für eine Simulation am VC20. Andere Geschichte, ...
Eventuell erkläre ich das hier noch mal später mit einer anderen Analogie.
Und damit klar ist, dass ich nicht nur schwurble, zwei Grafiken die ich mal erstellt habe, um das zu erklären:
Ja, schaut ganz wild aus, will ich jetzt mal eben auch nicht erklären, nur damit klar ist, dass ich hier Euch nicht was vom Pferd erzähle. Und nur ganz kurz, die Grafiken zeigen aus zwei Systemen, wie zwei Raumschiffe aneinander vorbeifliegen, oder anders, ein Raumschiff (solang wie der Abstand Erde/Mond) fliegt an Erde/Mond vorbei. Im Grunde haben wir einfach zwei gleichlange Abstände, zwei "Stäbe" die vorne und hinten je eine Uhr haben, die treffen sich, bei E0 also dem Ereignis V/E und dann geht es eben so lustig weiter. Nebenbei sind es auch Animationen, steckt schon einiges an Arbeit drin.
Egal, wird Euch so erstmal kaum helfen, wenn die Grundlagen nicht klar sind, ansonsten sind da alle Rechnungen und Werte drin.
Tut mir leid, ich kann es nicht anders sagen, das bringt so einfach nichts. Die Aussage hängt einfach frei in der Luft, ist wirklich nicht böse gemeint. Wir brauchen Punkte in einem Koordinatensystem, ein Punkt hat Koordinaten, also x, t zum Beispiel. Dann können wir das - erstmal nur Newton mit zwei Systemen S und S' machen, die zueinander bewegt sind und schauen uns einfach mal Punkte an. In der SRT nennt man so einen Punkt auch Ereignis. Also Raumschiff vorne trifft eben die Erde, das ist ein Ereignis, ein Punkt in der Raumzeit.
Damit es einfacher ist, setzt man hier in beiden Systemen S und S' den Nullpunkt, also x, t, x', t' = 0. Bedeutet, da ist eben 0 und beide Uhren dort zeigen 0 an. Man sollte bedenken, die Uhren sind nur Messgeräte, die auch virtuell sein könnten, es geht hier einfach um die Koordinatenwerte in S und S' für ein Ereignis, ein Punkt in der Raumzeit.
Nun kann man sich ein anderen Punkt in der Raumzeit anschauen, in den beiden Minkowski-Diagrammen ist das zum Beispiel E3, Raumschiff Vorne trifft den Mond (die Abstände sind nicht von mir, ein geistig nicht ganz so Bedachter, hat die mal vorgegeben, ich habe es dann nur dargestellt) die Uhr auf dem Mond zeigt nun 27 s an, die im Raumschiff nur 20 s.
Kurze Erklärung, erste Grafik zeigt das aus Sicht Erde/Mond, hier ist das Raumschiff bewegt, zweite Grafik zeigt das aus der Sicht des Astronauten im Raumschiff, hier sind Erde/Mond bewegt.
Der auf dem Mond kann nun sagen, ja die Uhr im Raumschiff ging doch langsamer, sie hat nur 20 s gezählt, meine aber 27 s, also q.e.d. und aus die Maus.
Nein, der im Raumschiff sieht es anders, der sagt nun, ja wir sind uns über die Anzeigen der Uhren bei E0 und E3 einig, beim Treffen am Mond zeigt die Uhr vorne im Raumschiff wirklich 20 s an und die auf dem Mond zeigt auch 27 s an.
Aber, und das ist ein ganz großes aber, also die Uhr von der Erde sich mit der Uhr vorne im Raumschiff bei E0 getroffen hat, hat die Uhr auf dem Mond für mich in S' nicht 0 s angezeigt, sondern sie zeigte schon 12,19 s.
Für mich in S' ist die Gleichzeitigkeit anders, Du auf dem Mond oder auf der Erde sagst, ja die Ereignisse E0 und E1 sind gleichzeitig, für mich sind die Ereignisse E0 und E2 gleichzeitig, die Uhr auf dem Mond zeigte eben schon etwas an. Und nun sind genau 14,81 s vergangen, für den "Flug" des Mondes zu meinem Raumschiff vorne.
Wäre ja auch logisch, weil der Abstand Erde/Mond von 18,14 Ls durch die Lorentzkontraktion bei mir eben nur 13,44 Ls sind.
Der Lorentzfaktor ist für beide gleich, jeder "misst" die Uhr des anderen langsamer laufend, scherzhaft umgangssprachlich mal formuliert. Ganz deutlich, wir haben es immer mit Differenzen zu tun, einem Delta Δ einen Abstand, die Differenz zwischen zwei Koordinatenwerten in einem System, zwei Punkte, zwei Ereignisse. also eben Δt = t2 - t1 oder so.
Um das hier zu verstehen, muss man wirklich die RdG verstehen, die Relativität der Gleichzeitigkeit, die Zeitdilatation bei Bewegung ist relativ und ergibst sich so nur aus der RdG. Das wird erst anders, wenn die Rakete umdreht und zurückfliegt, aber bis man dahin kommt, muss das hier verstanden sein und das ist schon ein kleiner Weg.
Kommt auf die Besitzer an, Freunde und ich würden da kein Stück nicht streiten, für uns ist das klar. Die SRT ist in der Physik gerade hier noch echt einfach, ...
Wie gesagt, Versuche das so zu erklären, bringen nichts und es ist nicht wirklich schwer zu verstehen. Es kommt auf die Ausrüstung an und das Training, wenn man gute Schuhe hat, einen normalen Körper, kann man sich in einem Jahr auch fit für einen Marathonlauf machen, man wird nicht gleich Rekorde brechen, aber ins Ziel kommen. Wenn man aber die die richtigen Schuhe hat und kein Training, wird man schnell schlapp machen, und sagen, ist ja echt schwer.
Genau, so ist es, gibt schon was, dass sich Kausalität nennt, ...
Also nein, tut mir so leid. Doch Du, wir haben ganz fest definiert, was die Dauer der Sekunde ist, unabhängig vom Bezugssystem, man nimmt misst immer im eigenen Ruhesystem, hier zuerst die SI-Sekunde und dann kann man damit den Meter messen. Also mit Licht. Und aus die Maus, damit misst man eben Zeiten und Längen, also Abstände zwischen zwei Ereignissen im eigenen System, man misst da immer mit Sekunde und Meter. Man kann nun ein Abstand messen, in der Zeit oder auch im Raum, der in einem anderen Ruhesystem anders gemessen wird, ...
Egal, ich kann das alles gerne erklären, aber nicht nur, wer es verstehen will, muss hier auch selbst etwas machen und zwar die Grundlagen lernen, was ist ein Inertialsystem, ein Koordinatensystem, ein Punkt, ein Ereignis, was sind Abstände und wie berechnet man die richtig. Die beiden Grafiken sind für jene die das kennen und die Grundlagen verstehen recht einfach, für Euch vermutlich ein Topf Spagetti. :D
Nicht wirklich bei der SRT, da gibt es keine mentale Barriere, da reichen ganz einfache Grundlagen aus, ist ja nun die die QT.
Da hat sich kein Fehler eingeschlichen, es ist sogar noch recht einfach, besorge Dir die richtigen Schuhe, und mache etwas Training, und dann geht das, die SRT ist hier zumindest echt noch einfach. Spannend wird es, wenn Beschleunigung mit ins Spiel kommt, oder eben Rotation, was ja auch Beschleunigung ist. Aber das hier, ist wirklich noch einfach zu verstehen, mit etwas Übung. Sogar das Zwillingsparadoxon kann man noch recht einfach packen. Wenn man das hier gepackt hat.
