zaeld schrieb:
nocheinPoet schrieb:Ich will es noch mal deutlicher erklären, ohne groß Hoffnung zu haben, dass es richtig verstanden wird.
Das kann ich bestätigen, es war für mich völlig unverständlich, und ich habe mir wirklich Mühe gegeben und nicht nur kurz drüber geschaut:nocheinPoet schrieb:Wir haben eine Uhr C, die in S bewegt ist.
Und die Uhren A und B, welche an unterschiedlichen Orten in S ruhen.
- Es fehlt eine Skizze, wie der Versuch aufgebaut ist
Die Basis für die Grafik kommt von
Wikipedia, die haben da noch weniger als ich gezeigt.
zaeld schrieb:Bei deinem vorhergehenden Post hast du zwei lange Raumschiffe aneinander fliegen lassen, das versucht man in dem Diagramm wiederzufinden, aber es scheint sich um ein anderes Experiment zu handeln, zumindest sind in der Skizze keine langen Raumschiffe zu erkennen.
Im Grunde hat man wo immer besser etwas in jedem System, dass eine Länge hat und an jedem davon eine Uhr. Also vier Uhren in Summe. Ich nehme gerne erstmal ein vollsymmetrischen Aufbau der Szenerie, um zu zeigen, es gibt keines das ausgezeichnet ist.
Dabei ist es mir egal, ob man Raumschiffe, Züge, Raketen, oder was auch immer nimmt. Zug und Bahnhof ist wie Flugzeug und Flughäfen nicht so gut, erstmal geht jeder normal davon aus, Bahnhof und Flughäfen müssen ruhen und zeichnet so eben deren System als absolut ruhend aus, alles andere muss eben bewegt sein. Dass ist dann problematisch und bei Flugzeug braucht man dann zwei, für jede Uhr eines.
Oft wird ein Beispiel gezeigt, wo man nur eine Uhr hat, welche sich dann an vielen anderen Uhren vorbei bewegt, genau das hat leider auch Peter Kroll in dem einen Video gemacht und sagt auch noch was wie, der Astronaut könnte ja so nun sehen, dass seine Uhr langsamer als die Uhren läuft, an denen er vorbeikommt. Das ist einfach nur falsch, die Uhren an denen er vorbeikommt, sind für ihn bewegt und laufen in seinem System langsamer und nicht schneller, aber sie gehen zunehmend vor.
Man muss sich immer klar machen, dass man eine Uhr immer mit zwei anderen Uhren vergleich, eine am Start- und eine am Zielort.
Wegen der Relativität der Gleichzeitigkeit (RdG) gehen die Uhren am Start- und Zielort aber nur in dem System synchron, in dem beide ruhen. Im anderen System, sind beide bewegt und gehen nicht nur dilatiert, sondern auch asynchron.
Um das hier verstehen zu können, muss man erstmal beides deutlich unterscheiden können. Viele gehen eben davon aus, dass sie an Uhren vorbeifahren können, die an den Gleisen stehen, und die gehen alle gleich und sind synchronisiert, sind sie aber nur in dem System in dem sie ruhen.
Am Besten fangt man also mal mit der Synchronisation der Uhren an, wird hier recht gut erklärt:
https://www.katharinengymnasium.de/wolf/web/srt/gleichzeitigin2systemen.html
zaeld schrieb:Die rosa und grauen Rechtecke erzeugen den Eindruck, die beiden Uhren würden sich im selben Bezugssystem oder "Raumschiff" befinden, aber sie scheinen doch eher unterschiedliche Momente zu kennzeichnen, wo sich die Uhren treffen.
Sehr schön, dann kann ich das auch gleich mal präzisieren, alles befindet sich in unzähligen Bezugsystemen. Ganz deutlich, die beiden Uhren werden in Bezugssystemen beschrieben, sie können darin ruhen oder eine beliebige Geschwindigkeit haben. Also haben wir in jedem System, S und S' auch alle vier Uhren. Aber nur jeweils zwei sind dort ruhend und die anderen beiden bewegt.
Hab mal mit
Otto E. Rössler "disputiert", er war ja nicht nur gegen CERN und hat von Schwarzen Löchern geschwurbelt, er hat sogar vorm Europäischen Gerichtshof für Menschenrechte gegen die Inbetriebnahme vom LHC geklagt, nein er war ja auch gegen die Relativitätstheorie und hat im Blog von Jocelyne Lopez den Lauten gemacht. Und ist dann mit der "Dame" ätzend in den Blogs von Markus Pössel und Joachim Schulz aufgefallen. Und da haben wir uns dann getroffen, und er schrieb doch echt, man könnte von einem Bezugsystem ins andere schauen. Totaler Mumpitz, nun ja, ist länger her, das
Projekt G.O. Mueller ist ja nun wohl endlich Asche.
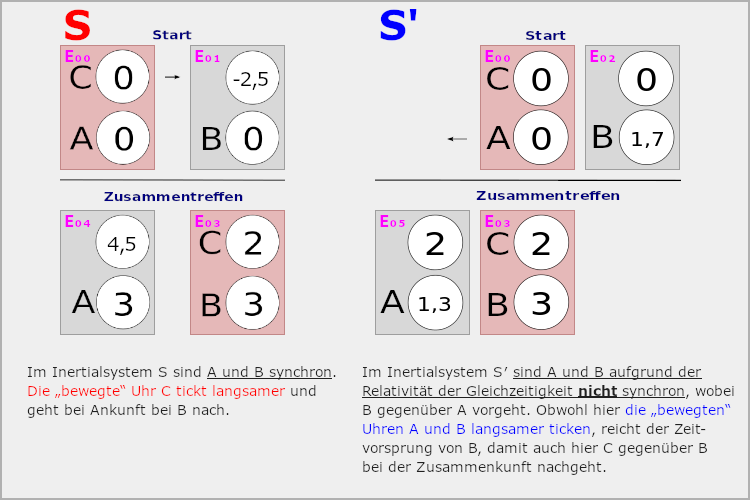
Zum Aufbau der Grafik aber zurück, linke Seite zeigt die Szene aus dem Ruhesystem S, oben Start, darunter Zusammentreffen.
Wir betrachten dabei immer vier Uhren, für ein Ereignis, einen Punkt in einem Koordinatensystem gibt es eine Orts- und eine Zeitkoordinate, gezeigt werden hier nur die Zeitkoordinatenwerte. Die Ereignisse sind nummeriert und immer eine Box, da treffen sich immer eine ruhende und eine im System bewegte Uhr, also bei
\color{#f0e0d0}\mathrm{E_{00}} ruht die Uhr A in S und Uhr C ist bewegt.
Beim Ereignis
\color{#f0e0d0}\mathrm{E_{01}} sehen wir wieder zwei Uhren, die eine ist nicht bezeichnet (nennen wir sie eben mal D), zeigt aber t' = - 2,5 an. Sie trifft sich in S bei t = 0 mit Uhr B.
Also in S ruhen die Uhren A, B und C, D sind bewegt.
In S gehen A und B synchron, C und D wegen der RdG asynchron, der Link oben zeigt aber recht gut, warum das so ist.
Kurze Erklärung noch, normal werden oft nur die Ereignisse mit rotem Hintergrund gezeigt, dass ist aber einfach zu wenig, um die Symmetrie der Zeitdilatation verstehen zu können.
Links unten, das Zusammentreffen, hier schauen wir uns erstmal Ereignis
\color{#f0e0d0}\mathrm{E_{04}} an. Uhr A ruht weiter in S, bedeutet
\color{#f0e0d0}\mathrm{x_{00}=x_{04}}.
Nun sehen wir über A eine Uhr, die wieder keine Bezeichnung hat, nennen wir sie mal Uhr E. Diese Uhr befindet sich in dem Abstand hinter der Uhr C, wie die Uhr D sich vor Uhr C befindet. Und ich habe die Grafik nur erstellt, um jemanden das von Wikipedia zu erklären, aber im Grunde sollte man da gleich Minkowski-Diagramme für nehmen. Wäre es also ganz meine Arbeit gewesen, hätte ich die Uhr E ganz sicher überall gezeigt.
Aber kurz zur Erklärung, wir haben also ein Kette von Uhren E, C, D und in S zeigen die eben bei
\color{#f0e0d0}\mathrm{t_{00}} die Zeiten E = 2,5 dann C = 0 und E = - 2,5 an.
Und ja, da braucht es dann noch ein weiteres Ereignis, müsste dann
\color{#f0e0d0}\mathrm{E_{\text{-} 01}} sein und würde oben vor
\color{#f0e0d0}\mathrm{E_{00}} liegen. Und ja, dann brauchen wir da auch noch eine weitere Uhr, und weil das dann immer mehr und komplexer wird, habe ich die Grafik hier nicht weiter groß aufgebohrt und nahe der von Wikipedia gelassen.
Gut, wir waren aber ja schon beim Zusammentreffen,
\color{#f0e0d0}\mathrm{E_{04}} zeigt eben Uhr A auf der 3 Einheiten vergangen sind und Uhr E, auf der eben 2 Einheiten vergangen sind.
Nun Ereignis
\color{#f0e0d0}\mathrm{E_{03}}, Uhr C trifft Uhr B, auf Uhr C sind wie auf allen in S bewegten Uhren E, C, D die 2 Einheiten vergangen, sie zeigt nun eben 2 an.
Nun müssen wir den Spaß mal aus S' anschauen (rechte Seite), dem Ruhesystem der Uhren E, C, D wo die alle synchron gehen und die Uhren A, B ... bewegt sich und somit asynchron gehen.
Wir fangen oben wieder mit Ereignis
\color{#f0e0d0}\mathrm{E_{00}} an. Das ist das Ereignis, was wir ja schon aus S kennen, Uhren A und C treffen sich, ein Ort, ein Punkt, ein Ereignis, alle sind sich einig, beide Uhren zeigen 0 Einheiten an, Drops gelutscht.
Ereignis
\color{#f0e0d0}\mathrm{E_{02}}, hier sehen wir wieder Uhr D, die zeigt dieses mal aber t' = 0 an. Das ist hier ein Ereignis, was wir so bisher noch nicht gesehen haben, in S wird das nicht gezeigt. In S auf der linken Seite sehen wir nur zwei Ereignisse bei t = 0 und zwei bei t = 3. Aber
\color{#f0e0d0}\mathrm{E_{02}} zeigt uns t = 1,7.
Ich habe das hinzugefügt, um zu zeigen, dass die Uhren A und B in S' eben asynchron laufen, zwei Ereignisse
\color{#f0e0d0}\mathrm{E_{00}} und
\color{#f0e0d0}\mathrm{E_{02}} sind in S' gleichzeitig, aber eben ungleichzeitig in S.
Nun noch das Zusammentreffen in S'.
Ereignis
\color{#f0e0d0}\mathrm{E_{05}} zeige ich auch wieder extra, eben um die Uhr A zu zeigen, gleichzeitig mit dem Ereignis Ereignis
\color{#f0e0d0}\mathrm{E_{03}} in S'. In S' gehen ja alle Uhren die da ruhen synchron, also E, C, D zeigen immer gleichzeitig gleiche Werte an. Darum sind beide eben bei 2.
Aber, und das ist ein großes aber, wir können auf Uhr A nun direkt ablesen, wie viele Zeiteinheiten die Uhren A und auch B während ihrer Bewegung in S' hochgezählt haben, in den 2 Zeiteinheiten die Uhr C und auch E, D gezählt haben. Nämlich genau 1,3 Einheiten.
Schauen wir noch mal eben darüber auf
\color{#f0e0d0}\mathrm{E_{02}}, hier zeigt Uhr B = 1,7 Einheiten an, dann darunter bei
\color{#f0e0d0}\mathrm{E_{03}} zeigt B = 3 Einheiten an, also hat auch sie nur 1,3 Einheiten hochgezählt.
Das muss so sein, weil die Uhren A und B eben in S' die bewegten Uhren sind und die müssen dilatiert laufen, in den 2 Einheiten welche die Uhr C nun für die Bewegung der Uhren A und B zählt, müssen diese weniger zählen, eben nur 1,3 Einheiten.
zaeld schrieb:Warum die eine Uhr auf - 2,5 steht, ist nicht erklärt.
Sie geht als in S bewegte Uhr asynchron zur Uhr C. Ergibt sich aus der RdG, wenn Du wissen willst, wie sich der Wert genau errechnet, zeige ich das gerne, eventuell am Ende des Beitrages.
zaeld schrieb:Geschwindigkeiten, Längen etc. sind nicht erklärt.
Kann man aber relativ einfach errechnen.
Rechnung:
\color{#f0e0d0}\mathrm{\Delta t = t_{03} - t_{00} = 3} \color{#f0e0d0}\mathrm{\Delta t' = t'_{03} - t'_{00} = 2} \color{#f0e0d0}\mathrm{\Delta t' = 2 = \tau} \color{#f0e0d0}\mathrm{\Delta t = \gamma \, \Delta \tau \Rightarrow \gamma = \frac{\Delta t}{\Delta \tau} = \frac{3}{2} = 1{,}5} Erklärung:
Wichtig hier zu verstehen, Eigenzeit
\color{#f0e0d0}\mathrm{\tau} ist die Zeit, welche eine Uhr misst, die Uhr, die bei jedem Ereignis anwesend ist, dass ist nur Uhr C. Messen wir eine Zeitdifferenz mit zwei unterschiedlichen Uhren, eben A und B, haben wir keine Eigenzeit, sondern Koordinatenzeit. Und das ist unabhängig vom System. Oft wird Eigenzeit falsch verstanden und gedacht, das ist die Zeit die im Ruhesystem gemessen wird. Ist es nur, wenn auf derselben Uhr gemessen wird. Und ja, im Ruhesystem zeigen die Uhren A und B schon immer denselben Wert an, weil sie synchron gehen, per Definition ist die Differenz der Zeiten beider Uhren aber Koordinatenzeit.
Geschwindigkeit:
\color{#f0e0d0}\mathrm{\gamma = \frac{1}{\sqrt{1 - v^2/c^2}} \Rightarrow v = \frac{\sqrt{5}}{3} \,\hspace{1px}c \approx 0{,}745 \,\hspace{1px}c} Wir kenne nun die Geschwindigkeit, nehmen wir mal als Zeiteinheit für das Beispiel die Sekunde s, dann kennen wir nun auch den Abstand zwischen den Uhren A und B mit 2,237 Ls. Und wenn wir das Ereignis
\color{#f0e0d0}\mathrm{E_{00}} als Nullpunkt beider Systeme S und S' definieren, kennen wir damit auch die Ortskoordinaten der Uhr B in S mit x = 2,237 Ls.
Da wir nun x, t von \color{#f0e0d0}\mathrm{E_{01}} kennen, können wir mit der Lorentztransformation auch noch x' und t' berechnen:
\color{#f0e0d0}\mathrm{x' = \gamma\,(x - v t) \Rightarrow x'_{01} = \frac{3}{2}\left(\sqrt{5} - \frac{\sqrt{5}}{3}\cdot 0\right) \approx 3,354\hspace{1px}Ls} \color{#f0e0d0}\mathrm{t' = \gamma\,(t - v x) \Rightarrow t'_{01} = \frac{3}{2}\left(0 - \frac{\sqrt{5}}{3}\cdot \sqrt{5}\right) = - 2,5\hspace{1px}s} Soweit so gut, machen wir es eben noch rund, uns fehlt ja nur noch t' für \color{#f0e0d0}\mathrm{E_{04}}. Also warum da über Uhr A eine namenlose Uhr mit 4,5 s ist:
\color{#f0e0d0}\mathrm{t' = \gamma\,(t - v x) \Rightarrow t'_{04} = \frac{3}{2}\left(3 - \frac{\sqrt{5}}{3}\cdot \sqrt{5}\right) = 4,5\hspace{1px}s} Damit ist der Drops nun für die linke Seite für jeden Wert gelutscht.
Gehen wir nun noch mal "kurz" rechts rüber und schauen uns das in S' an.
Die ganzen Werte für die beiden Ereignisse
\color{#f0e0d0}\mathrm{E_{00}} und
\color{#f0e0d0}\mathrm{E_{03}} haben wir ja schon berechnet, wir kennen nun ja auch den Ort der Uhr B in S und auch in S'. Nun müssen wir nur noch
\color{#f0e0d0}\mathrm{E_{02}} und
\color{#f0e0d0}\mathrm{E_{05}} klären.
Ich habe hier die LT schon hingeschrieben, die kann man auch umstellen und von S' nach S transformieren. Ich will das nun nicht noch vorrechnen und gebe mal die Werte hier einfach an.
Die Anzeige von Uhr B bei
\color{#f0e0d0}\mathrm{E_{02}} kennen wir schon mit t ≈ 1,7 (1,66666 ...) und uns fehlt nur noch x' = 1,49 Ls.
So und wer es richtig fett drauf hat, der zeigt noch mal eben, warum
\color{#f0e0d0}\mathrm{\gamma = 1,5} ist und das aus dem System S' heraus. Um hier vor der Klarheit mal erst etwas Verwirrung zu stiften, da könnte doch nun wer fragen, ja in S' vergeht ja nun nur 2 s und in der Zeit bewegt sich die Uhr B ja zur Uhr C. Die Uhr B zählt als bewegte Uhr nun aber nur 1,3333 s da kommt doch so dann gar nicht
\color{#f0e0d0}\mathrm{\gamma = 1,5} raus?
Ja, ich darf auch mal was fragen und nicht nur erklären.
Und für alle hier, die das Stück für Stück aufs Auge haben wollen:
Relativitätstheorie, Zeitdilatation ganz einfach erklärt.Aber leider sind da dann alle gleich wieder ausgestiegen, mir soll es egal sein, ich turne da nur nicht für mich allein vor. Wenn da aber echtes Interesse ist und gezeigt wird, mach ich gerne weiter.
zaeld schrieb:Als Ergebnis wird B = 3 s, C = 2 s präsentiert, wie es dazu kommt, wird nicht erklärt.
Ich denke mal, ich habe das nun doch sehr ausführlich erklärt, aber wenn noch was unklar ist, einfach fragen.
zaeld schrieb:Ich hatte noch versucht, mir das irgendwie zusammenzureimen, aber keine Chance. Gerade bei der Relativitätstheorie muss man wirklich jeden Schritt einzeln erklären, weil das so gehirnzermarternd ist. Und die RT ist mir gar nicht mal so fremd, von der Schule in Leistungskurs Physik und dann immer mal wieder, aber es bleibt schwer begreifbar. Ich fange im Prinzip immer wieder bei fast 0 an.
Ja, ich kenne das, wenn man sich damit mal eben zehn Jahre nicht weiter beschäftigt, dann geht schon was verloren. Also keiner soll hier glauben, ich bin ein Altruist und nur nett, und mache das hier um Wissen zu vermitteln, kein Stück nicht, das geht nur um mich, ich brauche nur eine Ausrede, warum ich das mache, damit ich es selbst mal wieder vertiefen und festigen kann. Wer mich hier im Forum länger kennt, weiß ich bin echt ein Misanthrop.
zaeld schrieb:nocheinPoet schrieb:Wir bleiben zuerst im Raumschiff A, ruhend in S. Wir sind vorne, Raumschiff B kommt vorbei, beide vorderen Enden treffen sich, die Astronauten in jeder Rakete vorne winken sich zu. Zeigen ihre Uhren und starten die beide bei 0 s. Das machen die Astronauten in jedem Raumschiff auch hinten so mit ihren Uhren. Bedeutet, die Uhren Vorne und hinten in A sind synchronisiert und die Uhren in Raumschiff B auch.
Was heißt das, sie sind synchronisiert? Wenn die beiden Bugs/Buge/Bugdinger der beiden Raumschiffe aufeinandertreffen, werden die Uhren vorne (kein Problem) und gleichzeitig hinten (woher wissen die, dass sich die Buge treffen?) gestartet?
Hab ich hier weiter oben erklärt und das Beispiel wird im anderen Thread viel genauer abgearbeitet, wenn es dann wen gibt, der Interesse zeigt.
zaeld schrieb:Das soll jetzt keine vernichtende Kritik sein, sondern nur aufzeigen, wo es mit dem Verständnis hapert. Vielleicht wird die Erklärung einfacher, wenn man von den Extremeffekten der RT weggeht und das einfach mal mit simplen, nachvollziehbaren Werten durchexperimentiert?
Zum Beispiel:
- Länge der Raumschiffe: 2 Lichtsekunden
- Geschwindigkeit des einen Raumschiffs: Halbe LG
- Relativistische Effekte bei 1/2 LG: Genau 1/2, also Uhren gehen halb so langsam
Ich habe gerade keine Ahnung, ob das mit diesen Werten zumindest konzeptuell funktioniert, oder ob man immer die Lorentz-Transformation benötigt. Aber das wäre mein Vorschlag.
Im Grunde ist es egal, wie lang man was macht, die Geschwindigkeit sollte aber über 0,6 c liegen. So oder so kann man das aber alles zeigen, nur hat man dann eben Differenzen von ns und nm.
