Eine Frage zu Einstein und seiner Relativitätstheorie

nocheinPoet schrieb:Solche Dinge verwirren vermutlich mehr, also sie hier denen helfen, die da noch im Nebel stehen.

Weiss ich nicht, klingt doch einfacher als Deine Erklärungen, die man nur als naturwissenschaftlicher Akademiker versteht. Ich fliege frotal auf einen Stern zu, der wird vor mir immer größer und ich bin nach 1,2 Monaten dort (am besten ohne direkt heinzufliegen). Da ich so schnell war, habe ich in meinem Zeitsystem die Entfernung scheinbar mit 10facher Lichtgeschwindikeit zurückgelegt. Erst wenn ich dort angehalten habe stelle ich fest, dass alles um mich herum leider ein Jahr älter ist und ich meine Uhr neu stellen muss.

Stellt sich nur noch die Frage, wenn ich kurz darauf mit der gleichen Geschwindigkeit wieder zurückfliege, sind die zwei Jahre Garantie auf das Raumschiff, das beim Start brandneu war, bei meiner Rückkehr auf die Erde schon abgelaufen? Schließlich hatte ich es kaum 3 Monate in Gebrauch. Aber die Halsabschneider beim Hersteller behaupten es sei schon über zwei Jahre alt.

Nebenbei, ich habe da eine spannende eigene Version vom Zwillingsparadoxon entwickelt:

Das Zwillingsparadoxon mit konstanter Beschleunigung. Ein Raumschiff (der Reisende) kommt mit 0,8 c an der Erde vorbeigeflogen und beschleunigt ständig mit 1 g entgegen der Flugrichtung. Er entfernt sich also von der Erde aus gesehen erstmal, wird dabei aber immer langsamer. Nach einer Weile hat er die 0,8 c abgebaut und beschleunigt nun auf die Erde zu. Irgendwann kommt er dann wieder mit einer bestimmten Geschwindigkeit an der Erde vorbei.
 
Warum ich mir das überlegt habe?
 
Weil sich hier nichts ändert, wir haben eine ständig konstante Beschleunigung, Die Richtungsänderung ist bezugssystemabhängig, ist von der Erde aus so. Der Reisende könnte ja auch nichts von der Erde wissen, er beschleunigt einfach stetig mit 1 g in eine Richtung.
 
Man könnte es so machen, dass die Erde zufällig gerade am Reisenden vorbei kommt, als dem seine Uhr 0 anzeigt und die auf der Erde auch. Dann kann man später, wenn der Reisende wieder an der Erde vorbeikommt, beide Eigenzeiten der Uhren vergleichen.

Es ist schon interessant, weil der auf der Erde sagt, mir ist alles egal, ich ruhe hier in meinem Ruhesystem, nichts geht ab. Und der in der Rakete sagt, mir ist auch alles egal, meine Triebwerke laufen, ich habe hier 1 g, werde beschleunigt und eben "schneller", alles cool. Und dann schaut er aus dem Fenster und sieht mal eben die Erde an sich vorbeifliegen. Und nach einer Weile kommt die wieder zurück und fliegt an seinem Fenster vorbei, in die andere Richtung. Aber keiner von beiden hat sich wo verändert, ...

Und es ist noch viel cooler, denn der auf der Erde spürt durch die Gravitation auch konstant 1 g. Genau wie der im Raumschiff. Wenn wir das in die Allgemeine Relativitätstheorie schieben, dann sollten beide in einer geschlossenen Kiste gar nicht unterscheiden können, wer nun auf der Erde und wer nun im Raumschiff ist.

Um das hier nun aufzudröseln, muss man schon etwas mehr verstanden haben, weil wir haben hier einen Zeitunterschied, der muss dann mal begründet werden.

JosephConrad schrieb:Weiss ich nicht, klingt doch einfacher als Deine Erklärungen, die man nur als naturwissenschaftlicher Akademiker versteht.

Unfug, ich habe eine Erklärung, sogar einige, Du hast nur eine recht einfache Beschreibung, die mal gar nichts erklärt, und auch nur extrem allgemein gehalten ist. Wo bitte soll das was genau nun wie genau erklären?

Eben, da ist nichts mit Erklärung.

---

JosephConrad schrieb:Ich fliege frontal auf einen Stern zu, der wird vor mir immer größer und ich bin nach 1,2 Monaten dort. Da ich so schnell war, habe ich in meinem Zeitsystem die Entfernung scheinbar mit 10facher Lichtgeschwindigkeit zurückgelegt. Erst wenn ich dort angehalten habe stelle ich fest, dass alles um mich herum leider ein Jahr älter ist und ich meine Uhr neu stellen muss.

Wenn dann heißt es Bezugsystem oder Inertialsystem und nein, in Deinem System legst Du mal gar keine Entfernung zurück, weil Du in Deinem System per Definition ruhst. Darum nennt man es auch Ruhesystem.

Eine Entfernung legst Du nur in einem anderen System zurück, dem der Erde, dem vom Stern, aber nie in Deinem eigenen.

Ja, so schaut es aus, darum bringt Deine "Erklärung" mal gar nichts, wobei, es ist ja eh keine.

---

JosephConrad schrieb:Stellt sich nur noch die Frage, wenn ich kurz darauf mit der gleichen Geschwindigkeit wieder zurückfliege, sind die zwei Jahre Garantie auf das Raumschiff, das beim Start brandneu war, bei meiner Rückkehr auf die Erde schon abgelaufen? Schließlich hatte ich es kaum 3 Monate in Gebrauch. Aber die Halsabschneider beim Hersteller behaupten es sei schon über zwei Jahre alt.

Echt jetzt? Eventuell versuchst Du es doch mehr im Bereich Unterhaltung und nicht hier im Bereich Wissenschaft? Nur so eine Idee von mir. ;)

Rindler-Hyperbel in der Minkowski-Raumzeit.

„Der auf der Erde spürt durch die Gravitation auch konstant 1 g.“ Das ist nur lokal richtig. Das Äquivalenzprinzip sagt: In einem kleinen Labor für kurze Zeit ohne Gezeitenkräfte kann man Gravitation und Beschleunigung nicht unterscheiden. Aber global gilt das nicht.

@JosephConrad

Cool, nach dem was Du davor geschrieben hast, ist das ja klar, immerhin fandest Du meine Frage so interessant, dass Du sie in eine KI kopiert hast. GPT oder Grok? Wo war er denn? :D

Und lass mich mal raten, Du verstehst kein Wort davon, oder sagt Dir Rindler-Hyperbel in der Minkowski-Raumzeit irgendetwas? Auch das Äquivalenzprinzip ist Dir vermutlich nicht so wirklich ein Begriff?

Ich will nicht stänkern, echt nicht, mein Beispiel war aber zum Grübeln hier gedacht, nicht um es eben von einer KI durchatmen zu lassen. :D

Wer sich wundert, stellt Fragen, oft bringt das dann wen dazu, Dinge zu lernen.

Die Minkowski Metrik hast du ja vorhin schon erklärt gekrümmte Linien - Beschleunigung. Und wenn der Beobachter mit konstanter Beschleunigung unterwegs ist, dann beschreibt er eine Hyperbel.

Ach ja, vielleicht benutzt du ja eine KI?

@JosephConrad

Klar benutze ich auch KI, immer wieder mal, jeden Tag. Aber nicht so, wie Du eventuell vermutest. Meine Erklärungen sind ja alle von mir, ich habe das mir alles über 20 Jahre erarbeitet, da gab es noch keine KI. Die Grafiken, die ich erstellt habe und hier und im anderen Thread zeige, hab ich fast alle erstellt, bevor es KI gab.

Und nein, offenbar hast Du wieder zur KI gegriffen, bei Minkowski Metrik, ich habe nichts von gekrümmter Linie geschrieben oder Beschleunigung vorhin. Offenbar hast Du im selben Chat der KI weitergemacht und nun nach Minkowski Metrik gefragt. Da davor ja was mit konstanter Beschleunigung gewesen ist, kommt die KI nun mit gekrümmter Linie daher.


Ich hatte nur das vorhin geschrieben:

nocheinPoet schrieb:Noch eine wichtige Erklärung, dass ist eine Analogie, sie bricht mit der Metrik, die Metrik auf dem Parkplatz ist euklidisch, es ist keine Minkowski-Metrik. Darum zeigt das Messrad von Deinem Freund nun auch 20 m an, auf dem Parkplatz im Raum ist das richtig, aber nicht bei einer Minkowski-Metrik weil da nicht c² = a² + b² = 10² = 5² + 8,666². Da haben wir dann nämlich ds² = dt² - dx² also ds² = dt² - dx² = τ² = dt² - dx² = 10² - 5² = 100 - 25 = 75.

Warum schreibt Dir nun Deine KI was von gekrümmte Linien?

Damit Du das verstehst, in einem Minkowski-Diagramm aber auch einem normalen Weg/Zeit Diagramm, ist eine Beschleunigung eben eine gekrümmte Linie.


Bildquelle: https://wiki.pruefungshefte.de/de/physik/beschleunigte-bewegungen/zeit-weg-diagramm

Also, die krumme Linie hat nichts mit der Minkowski Metrik zu tun. Es geht da um den Pythagoras, da gilt eben ds² = dt² - dx² und nicht ds² = dt² + dx². Aber denke mal, dass wird Dir auch nicht wirklich was erklären.

nocheinPoet schrieb:Und nein, offenbar hast Du wieder zur KI gegriffen, bei Minkowski Metrik, ich habe nichts von gekrümmter Linie geschrieben oder Beschleunigung vorhin. Offenbar hast Du im selben Chat der KI weitergemacht und nun nach Minkowski Metrik gefragt. Da davor ja was mit konstanter Beschleunigung gewesen ist, kommt die KI nun mit gekrümmter Linie daher.

Nein, das habe ich hierher:

Die Hyperbelbewegung ist in der speziellen Relativitätstheorie die Bewegung eines Objekts mit konstanter Eigenbeschleunigung, wobei diese Beschleunigung von einem mitbewegten Beobachter mittels Beschleunigungssensor gemessen wird. Der Name Hyperbelbewegung folgt aus dem Umstand, dass die Gleichung für den Pfad dieses Objekts im Minkowski-Diagramm einer Hyperbel entspricht. Diese Bewegung hat einige interessante Eigenschaften, wie die Möglichkeit, das Licht hinter sich zu lassen, wenn ein genügender Vorsprung gegeben ist.[1] Für einen allgemeinen Überblick zu Beschleunigungen in der Minkowski-Raumzeit siehe Beschleunigung (Spezielle Relativitätstheorie).

Quelle: Wikipedia: Hyperbelbewegung#Weblinks

@JosephConrad

Ja, gut, aber bitte wie kommst Du ohne KI hier nun auf den Begriff "Hyperbelbewegung"? Ich hatte den nicht genannt. Also wird das ja wohl doch von der KI gekommen sein.


Du kommst hier erst mit:

JosephConrad schrieb:Rindler-Hyperbel in der Minkowski-Raumzeit.

„Der auf der Erde spürt durch die Gravitation auch konstant 1 g.“ Das ist nur lokal richtig. Das Äquivalenzprinzip sagt: In einem kleinen Labor für kurze Zeit ohne Gezeitenkräfte kann man Gravitation und Beschleunigung nicht unterscheiden. Aber global gilt das nicht.

Wo wohl recht sicher eine KI hinter steckt, dann schreib ich was und Du gehst mal eben auf Wikipedia zu "Hyperbelbewegung"? Was hast Du denn gegoogelt?

Aber auch egal, ist nun echt wo OT, bringt ja keinen hier weiter.

nocheinPoet schrieb:Solche Dinge verwirren vermutlich mehr, also sie hier denen helfen, die da noch im Nebel stehen.

nocheinPoet schrieb:bringt ja keinen hier weiter.

Also doch:

JosephConrad schrieb:Deine Erklärungen, die man nur als naturwissenschaftlicher Akademiker versteht.

Und selbst wenn irgendwoher Antworten kommen, bist Du beleidigt weil ja eigentlich das knifflige Rätsel außer Dir keiner verstehen kann und natürlich jede KI. Frei nach Lichtenberg "Wir haben keine Worte mit dem Dummen von Weisheit zu sprechen. Der ist schon weise, der den Weisen versteht“

Und weil das alles so ist, klingt das hier im Thread zur initialen Frage

kaktuss schrieb am 11.12.2025:Eine bewegte Uhr geht langsamer als eine unbewegte.
Für eine bewegte Person vergeht die Zeit langsamer relativ zu einer unbewegten Person.
Die bewegte Person nimmt die Zeit aber normal schnell wahr, friert also nicht ein...
Nun die Uhr aus Satz 1 oben friert aber ein, also geht wirklich langsamer.

Kann mir das bitte mal jemand erklären ?

schon ein wenig, verzeih mir den Ausdruck, nach "Selbstbeweihräucherung".

Vorgestern hatte ich geschrieben:

Lupo54 schrieb:Kann man sagen: "jede Bewegung verlangsamt die Zeit"?

Nach reiflicher Überlegung bin ich nunmehr der Meinung dass es nicht die Bewegung ist, die auf die Zeit wirkt, sondern die Schwerkraft. Die bei Beschleunigung/Verzögerung entsteht. Aber auch sozusagen statisch (ohne Bewegungsänderung) als Gravitation vorhanden ist bei Massen.

Lupo54 schrieb:Nach reiflicher Überlegung bin ich nunmehr der Meinung dass es nicht die Bewegung ist, die auf die Zeit wirkt, sondern die Schwerkraft. Die bei Beschleunigung/Verzögerung entsteht.

Bei Beschleunigung entsteht ja immer als Abfallprodukt Bewegung ("Geschwindigkeit").
Dabei entsteht eigentlich keine "echte" 3-dimensionale,
sondern nur eine 1-dimensionale "Schwerkraft", in Gegenrichtung der Bewegung.

Lupo54 schrieb:Nach reiflicher Überlegung bin ich nunmehr der Meinung dass es nicht die Bewegung ist, die auf die Zeit wirkt, sondern die Schwerkraft. Die bei Beschleunigung/Verzögerung entsteht.

Bei Beschleunigung entsteht ja immer als Abfallprodukt Bewegung ("Geschwindigkeit").
Dabei entsteht eigentlich keine "echte" 3-dimensionale,
sondern nur eine 1-dimensionale "Schwerkraft", in Gegenrichtung der Bewegung.

JosephConrad schrieb:Also doch:

JosephConrad schrieb:Deine Erklärungen, die man nur als naturwissenschaftlicher Akademiker versteht.

Und selbst wenn irgendwoher Antworten kommen, bist Du beleidigt ...

Blödsinn, doppelt, weißt Du, eventuell ist das für Dich ja eine "Lösung", hier die naturwissenschaftlicher Akademiker ganz weit nach oben zustellen, damit Du Dich selbst bei "normal" verorten kannst, aber an dem ist es nicht. Was ich hier so erklärt habe, zur SRT, oder zur RdG ist recht einfach, um das zu verstehen, braucht man nicht mal Abitur.


So was hier:

nocheinPoet schrieb:Zwei Züge treffen sich, gleich lang, mittig zwischen beiden schlägt ein Blitz ein. Das Lichtsignal läuft über gleiche Strecke zu den Enden der Züge. Im Zug A kommen beide Signale an den Enden von Zug A gleichzeitig an, die Uhren starten gleichzeitig, sind synchronisiert.

Für B sieht es in seinem Zug für seine Uhren genauso aus, aber für ihn ist Zug A bewegt, das Ende bewegt sich dem Signal entgegen, wird zuerst erreicht, die Uhr startet da als erstes. Die Lok bewegt sich vom Signal weg, das läuft hinterher, kommt später an, die Uhr startet also nach der im Heck, die Uhren in Zug A gehen für den im Zug B also nicht synchron, sie wurden nicht gleichzeitig gestartet, sondern nacheinander.

ist recht trivial, und ich hatte dazu noch Animationen und glaube sogar Videos verlinkt. Es geht hier nicht um die QFT oder die Maxwell-Gleichungen, oder die Dirac-Gleichung.

---

JosephConrad schrieb:... weil ja eigentlich das knifflige Rätsel außer Dir keiner verstehen kann und natürlich jede KI.

Was für ein Schwachsinn, das mit der konstanten Beschleunigung ist mir gestern einfach hier eben beim Schreiben eingefallen und das ist kein "kniffliges" Rätsel. Nebenbei, es ging mir darum, zu verstehen, dass Beschleunigung konstant ist, Geschwindigkeit aber relativ. Dass da so einer in seiner Rakete eben ständig beschleunigt, ohne Veränderung, und dann kommt von vorne die Erde am Fenster vorbei und fliegt davon und nach einer Weile kommt sie zurück und fliegt nach vorne davon.

Einige (hier wohl mehr) gehen davon aus, der Kerl in der Rakete muss doch "umgedreht" haben und dafür erst gebremst und dann wieder beschleunigt.

Ich wollte damit nur zeigen, dass Beschleunigung eben immer Geschwindigkeitsänderung ist, und Geschwindigkeit selbst vom Beobachtersystem abhängig.

Anderes Beispiel, fiel mir auch eben so ein, ein Tanker fährt auf einen Hafen zu, schnell und er lässt nun die Schraube rückwärts drehen, vom Hafen aus gesehen wird er langsamer. Kurz vorm Hafen hat er seine Geschwindigkeit - in Bezug zum Hafen - vollständig abgebaut und nun entfernt er sich wieder vom Hafen und das zunehmend schneller.

Der Tanker hat die ganze Zeit konstant beschleunigt für die Geschwindigkeitsänderung und vom Hafen aus betrachtet, gab es sogar eine Richtungsänderung. Aber die ist eben relativ, weil es die Geschwindigkeit selber auch ist. Hätte der Tanker also ein Schlauboot am Anfang mit gleicher Geschwindigkeit wie er selbst gegenüber dem Hafen hatte, hätte sich der Tanker vom Boot nur mit konstant zunehmender Geschwindigkeit entfernt.

Und das eben mit einem Beispiel, was noch ein echtes Zwillingsparadoxon ist. Ist es nämlich, und dann viel mehr erst auf, dass das sogar noch geiler ist, weil es doppelt eines ist, denn man kann die ART mitnehmen, denn der auf der Erde hat ja auch die ganze Zeit 1 g. Das aber im Rahmen der ART richtig zu lösen, ist schon eine ganz andere Hausnummer und das schüttle auch ich mir nicht eben aus dem Ärmel.

---

JosephConrad schrieb:Frei nach Lichtenberg "Wir haben keine Worte mit dem Dummen von Weisheit zu sprechen. Der ist schon weise, der den Weisen versteht“.

Höre doch echt mal auf, es ist hier was Du mir unterstellst, wenn Du Dich als Dummen sehen willst, Deine Sache, und ich habe mich nie als weise dargestellt. Ich weiß, was ich alles nicht weiß, ganz sicher.

---

JosephConrad schrieb:Und weil das alles so ist, ...

Ex falsō quodlibet (aus falschen folgt beliebiges), es ist nicht so, Du behautest etwas, dass ist nicht belegt und ist ganz klar ad hominem.

---

JosephConrad schrieb:... klingt das hier im Thread zur initialen Frage:

kaktuss schrieb am 11.12.2025:Eine bewegte Uhr geht langsamer als eine unbewegte. Für eine bewegte Person vergeht die Zeit langsamer relativ zu einer unbewegten Person. Die bewegte Person nimmt die Zeit aber normal schnell wahr, friert also nicht ein. Nun die Uhr aus Satz 1 oben friert aber ein, also geht wirklich langsamer. Kann mir das bitte mal jemand erklären?

... schon ein wenig, verzeih mir den Ausdruck, nach "Selbstbeweihräucherung".

Nein, Du drehst Dir da einen, und willst mir einen unterjubeln, alleine Dein Problem. Kann ich Dir erklären, wenn Du richtig liegen würdest, müsste man mit dem was ich schrieb, sich selbst beweihräuchern können, oder zumindest glauben, dass man das kann. Dass man damit nun ganz groß und toll und klug und wissend dasteht, den anderen überlegen.

An dem ist es nicht, denn da würde man sich kaum die Mühe machen, die Dinge so genau und mit so viel Zeitaufwand zu erklären, alleine daran solltest selbst Du erkennen können, mein Ziel ist hier ganz sicher nicht die Selbstdarstellung, sondern der aufrichtige Versuch hier anderen die etwas verstehen wollen, dabei zu helfen. Ich versuche hier Wissen zu vermitteln, ich habe etwas verstanden und versuche dieses Verständnis zu nutzen, um anderen Usern hier eben ihre Fragen so zu beantworten, dass sie was verstehen.

Okay?

Klappt nun aber nicht so wirklich gut, denn offenbar ist der Wunsch größer, als die Bereitschaft sich zu bewegen. Und nun wäre ich echt begeistert, wenn Du Dein Framing Dir sparen würdest, es "trifft" mich ja schon etwas, dass es hier nicht wirklich weitergeht, Dinge nicht verstanden werden, da musst Du nun nicht noch anfangen mich anzugreifen, mir Selbstbeweihräucherung unterstellen und versuchen mir an Bein zu pinkeln. Ja?

Lupo54 schrieb:Vorgestern hatte ich geschrieben:

Lupo54 schrieb:Kann man sagen: ... jede Bewegung verlangsamt die Zeit?

Nach reiflicher Überlegung bin ich nunmehr der Meinung dass es nicht die Bewegung ist, die auf die Zeit wirkt, sondern die Schwerkraft. Die bei Beschleunigung/Verzögerung entsteht.

Ich will das mal richtigrücken, also, die Schwerkraft entsteht nur durch Masse, nicht durch Beschleunigung. Du meinst hier etwas anderes. Aufgefallen, dass ich nicht mit "Nein, ..." den Satz begonnen habe?

Also, Schwerkraft erzeugt eine "Kraft", eine Kraft kann beschleunigen, wir haben eine Beschleunigungskraft. Keine Ahnung, wie Du nun dahin gekommen bist, die Überlegung selbst ist ja recht gut, der Begriff war nur nicht richtig. Ich hatte das hier gestern gerade in meinem Beispiel zum Zwillingsparadoxon mit konstanter Beschleunigung.


Es geht um das Äquivalenzprinzip:

Nach dem Äquivalenzprinzip der allgemeinen Relativitätstheorie lässt sich nicht unterscheiden, ob sich ein Beobachter auf der Erde befindet oder in einer Rakete, die im Weltraum mit Erdbeschleunigung g beschleunigt.

Quelle: Wikipedia: Beschleunigung#Äquivalenzprinzip und allgemeine Relativitätstheorie

Damit hatte ich ja gespielt, und das ist schon interessant. Und Du kannst nun stolz auf Dich sein, denn Deine Überlegung ist wirklich gut, Einstein selbst hat hier ja auch einen Zusammenhang gesehen, und ich es gestern angesprochen. Und es könnte so sein, ist es aber leider nicht.

Wenn Du richtig liegen würdest, dann würde in meinem Beispiel der Zwilling ja ständig beschleunigen, an der Erde vorbeikommen, seine Uhr mit der auf der Erde starten, und dann wieder bei der Erde vorbeikommen. Und beide haben immer nur 1 g an Beschleunigungskraft gespürt, dann müssten beide Uhren beim zweiten Treffen gleiche Eigenzeiten zeigen. Tun sie nicht, die in der Rakete zeigt wirklich weniger an.

Also, guter Ansatz, aber das ist es nicht.

@nocheinPoet

nocheinPoet schrieb:Ich habe das sooft schon erklärt, schreib ich einfach runter und hatte es hier auch schon erklärt.

Denke aber nicht, es wird nun helfen.

nocheinPoet schrieb:Ich kann nur nachfragen und dann die Dinge richtig beschreiben, wenn da dann wer Bock drauf hat. Wenn nicht, alles gut, hab ich kein Problem mit, bleibt es wie es ist und ich nutze meine Zeit anders.

nocheinPoet schrieb am 19.12.2025:Keine Ahnung, was Ihr hier versuchst, warum Ihr so hier Zeit verbrennt. Wer es nicht verstanden hat, kann es nicht erklären, selbst wer es verstanden hat, muss es nicht gut erklären können. Ich meine das nicht böse, aber es ist so, Ihr könnt eine Keule nicht sicher fangen und wollt dann mit vier Stück jonglieren. Wo ist da der Sinn?

nocheinPoet schrieb:Ja, so schaut es aus, darum bringt Deine "Erklärung" mal gar nichts, wobei, es ist ja eh keine.

nocheinPoet schrieb:Echt jetzt? Eventuell versuchst Du es doch mehr im Bereich Unterhaltung und nicht hier im Bereich Wissenschaft? Nur so eine Idee von mir. ;)

Der Ton macht die Musik. Deine Erklärungen sind wohl nur von den wenigsten zu verstehen, ich sehe das auch in Deinem Parallelthread, wo Du versprichtst Die Relativitätstheorie einfach zu erklären. Dort mutet Dein Appel an die Teilnehmer fast schon etwas verzweifelt an, doch die Grundlagen zu verstehen.

nocheinPoet schrieb am 15.12.2025:Auch wäre ich echt erfreut, wenn Ihr Euch mal den Fragen widmet, ist keine Pflichtübung, aber es wäre für mich hilfreich, damit ich weiß, was verstanden wurde, und was noch nicht.

Aber so wie Du versuchst diese zu vermitteln, ist das mMn. viel zu akademisch. Auch wenn Du sagst man kann das auch ohne Abitur verstehen, wil alles "recht einfach" ist, so habe ich meine Zweifel, wenn ich Deine Grafik sehe, auf der gefühlt 100 Ereignisse vermerkt sind. Ist meine pers. Ansicht.

Indem Du aber die Erklärungshoheit an Dich reißt und z.B. versuchst meine Erklärung lächerlich zu machen, die aus der Sicht des Reisenden dessen Eindrücke beschreibt, was vermutlich hier jeder sofort verstanden hat, begibst Du Dich in den Elfenbeinturm.

Das alles kannst Du negieren, hilft aber nicht weiter. Bitte denk' mal drüber nach.

JosephConrad schrieb:Der Ton macht die Musik. Deine Erklärungen sind wohl nur von den wenigsten zu verstehen, ich sehe das auch in Deinem Parallelthread, wo Du versprichst Die Relativitätstheorie einfach zu erklären.

Der Ton ist nicht das Problem, das ist Ehrlichkeit, kommen einige heute aber nicht mehr mit klar, nehmen es persönlich, und wollen eben lieber in Watte gewickelt werden. So bin ich nicht drauf, ich gebe auch meine Zeit her, es werden hier Fragen im Forum gestellt, ich antworte, wer fragt und eine Antwort erwartet, sollte sich dann auch die Zeit nehmen, sich damit zu beschäftigen.

Das ist offenkundig aber nicht der Fall, es wird erwartet, dass man es nicht nur vorgekaut bekommt, sondern gleich noch verdaut, überlege mal, da hat wer eine Frage zu etwas, was wohl nicht ganz einfach zu verstehen für ihn ist. Dann kann er nicht erwarten, dass er drei einfache Sätze für Fünfjährige bekommt und in drei Minuten gehen nun für ihn alle Lichter an und die Groschen fallen.

Natürlich braucht es da auch Eigenleistung und natürlich dauert das etwas.

Wenn ich also hier nun Zeit gebe, und dann erkenne, nein, da wird mal selbst gar nichts gebracht von der anderen Seite, selbst echt einfache Fragen, werden ignoriert. Echt jetzt, im anderen Thread ging es nun wirklich ganz einfach los, ein Punkt in einem Koordinatensystem, das ist Mathematik Grundschule in der vierten Klasse. Wenn nicht früher. Da ging es noch um Grundlagenwissen, da war noch nichts mit Einstein und der Relativitätstheorie.

So, und dann schau mal hier, wenn Du mir nun Versagen unterstellst, oder ich hätte es nicht einfach genug vorgeturnt und nicht genug freundlich dabei gelächelt, dann sage mir mal, wer hat hier denn von den anderen nun was vorgeturnt, toll gelächelt und die Frage befriedigend für die Fragesteller beantworten können?

Wer von den Usern, die hier das nicht verstanden haben, haben nun dann etwas verstanden?
Und durch welche Erklärung und von wem?

Eben, Dunkeltuten, es wird weiter durch den Nebel gestolpert. Du kannst nicht in ein Fitnesscenter gehen, und erwarten Du bekommst nun Muskeln, wenn Du nur schaust, wie der Trainer die Übungen zeigt. Und der wird sich auch wo wann dann verarscht vorkommen, bedenke mal, das Training hier ist für lau, ich bekomme ja kein Geld dafür. Wenn wäre es etwas anders, dann wäre es kein Freundschaftsdienst an die Community sondern ein Geschäft.

---

JosephConrad schrieb:Dort mutet Dein Appel an die Teilnehmer fast schon etwas verzweifelt an, doch die Grundlagen zu verstehen.

Nein, Unfug, nicht verzweifelt, es war motivierend und etwas enttäuscht, ich habe mir mehr gerechnet, ich habe mit überhaupt etwas gerechnet, gab hier eine Zeit im Forum, da hatten die User etwas mehr an Respekt untereinander, und weißt Du, drauf geschissen, mich enttäuscht mehr die Welt mit den Menschen, man muss eben wohl wirklich seine Erwartungen sehr weit runterschrauben.

---

JosephConrad schrieb:

nocheinPoet schrieb am 15.12.2025:Auch wäre ich echt erfreut, wenn Ihr Euch mal den Fragen widmet, ist keine Pflichtübung, aber es wäre für mich hilfreich, damit ich weiß, was verstanden wurde, und was noch nicht.

Aber so wie Du versuchst diese zu vermitteln, ist das mMn. viel zu akademisch.

Ja, danke für Deine Meinung, hilfreich, mach es mal besser, bin gespannt. Zeige mir einen hier, der es besser macht, der sich überhaupt die Zeit nimmt, und es macht, bin gespannt.

Weißt Du, noch mal ganz deutlich, es hat mit Mathematik zu tun, das ist nun mal die Basis, es geht nicht ohne. Ich habe das schon ein paar mal geschrieben, die Erwartungshaltung ist offenbar, Muskeln bekommen ohne einen Finger zu bewegen, weil ist ja anstrengend. Das gehört zum Thema, es geht um Physik, um Physik die nach Newton kommt, es geht um die Relativitätstheorie.

Wie soll das verstanden werden können, wenn nicht mal die Physik von Newton verstanden wird? Und klar, bitte nicht rechnen, keine Begriffe wie Ereignis, Punkt, Koordinatensystem, gibt es nicht was dazu auf TikTok?

---

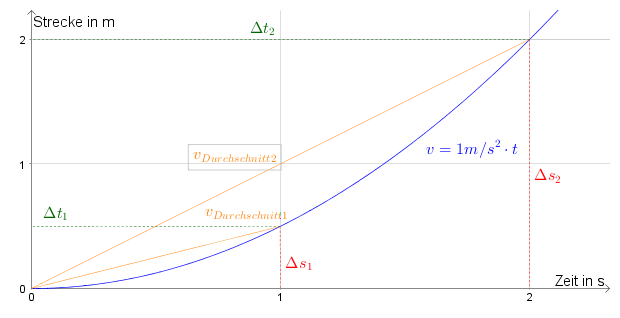
JosephConrad schrieb:Auch wenn Du sagst man kann das auch ohne Abitur verstehen, wili alles "recht einfach" ist, so habe ich meine Zweifel, wenn ich Deine Grafik sehe, auf der gefühlt 100 Ereignisse vermerkt sind. Ist meine pers. Ansicht.

Höre doch auf, meine Güte, hab ich gesagt, alles ansehen, oder habe ich erst nur einen Ausschnitt gezeigt, und gesagt, schaut Euch bitte nur zwei Ereignisse an, und da nur zuerst die Zeiten? Habe ich das nicht auch noch hingeschrieben? Mehrfach erklärt? Die großen Grafiken kamen, weil danach gefragt wurde, weil wer nicht das im Auge hatte, was ich ja erklärt habe. Warum auch auf das achten, was gerade Thema ist, man schaut sich eben alles andere an, nur nicht das, um was es gerade geht und was gerade erklärt wird. Klar, mach Dir alle Gewichte drauf und dann wirst Du scheitern. Und dann ist natürlich der Trainer schuld.

---

JosephConrad schrieb:Indem Du aber die Erklärungshoheit an Dich reißt und z.B. versuchst meine Erklärung lächerlich zu machen, die aus der Sicht des Reisenden dessen Eindrücke beschreibt, was vermutlich hier jeder sofort verstanden hat, begibst Du Dich in den Elfenbeinturm.

Unfug, ich reiße mal gar nichts an mich, ich will keine Erklärungshoheit, wusste nicht mal, dass es eine solche hier gibt. Und nun mache mal nicht die Mimose hier, und unterstelle mir nichts, ich versuche kein Stück nicht Deine Erklärung lächerlich zu machen, Du hast ja nicht mal eine Erklärung gehabt. Wo hast Du was denn erklärt?

Schau Dir mal die Definition von "Erklärung" und "Beschreibung" an, Du hast etwas beschrieben, nichts erklärt. Und wo ist nun Dein Erfolg? Wer versteht denn nun dank Dir die SRT und hat seine Fragen beantwortet bekommen? Wollen wir mal nachfragen, wie weit nun die Erklärung von Dir geholfen hat, die SRT zu verstehen?

---

Schauen wir uns doch mal ganz objektiv Deine "Erklärung" gemeinsam in der Retrospektive noch mal an:

JosephConrad schrieb:

nocheinPoet schrieb:Solche Dinge verwirren vermutlich mehr, also sie hier denen helfen, die da noch im Nebel stehen.

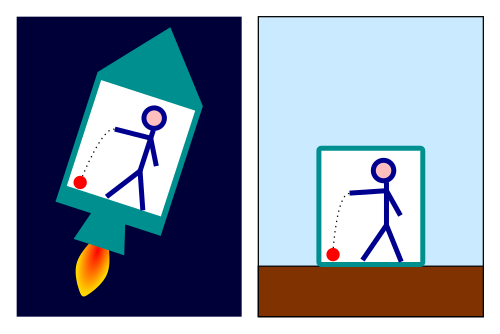
Weiss ich nicht, klingt doch einfacher als Deine Erklärungen, die man nur als naturwissenschaftlicher Akademiker versteht. Ich fliege frontal auf einen Stern zu, der wird vor mir immer größer und ich bin nach 1,2 Monaten dort ... . Da ich so schnell war, habe ich in meinem Zeitsystem die Entfernung scheinbar mit 10facher Lichtgeschwindigkeit zurückgelegt. Erst wenn ich dort angehalten habe stelle ich fest, dass alles um mich herum leider ein Jahr älter ist und ich meine Uhr neu stellen muss.

Darum ging es doch, oder? Also mehr "Erklärung" finde ich hier nicht von Dir. Aber erstmal das hier, als "Erklärung", weil Du so schnell warst, hast Du in Deinem "Zeitsystem" die Entfernung scheinbar mit 10facher Lichtgeschwindigkeit zurückgelegt. Klar, wenn das mal nicht alles erklärt, da bleiben zur SRT und der Zeitdilatation ja nun ganz sicher keine Fragen mehr offen.

Und nein, ich mache Dich damit nicht lächerlich, und nein, ich stelle mich auch damit nicht über Dich, ist versuche Dir die Augen für die Realität zu öffnen. Du meinst das sind Wanderschuhe und Du kommst damit auf den Everest? Nein es sind nur Hausschuhe. Und im T-Shirt wirst Du auch nicht durch den Schnee kommen. Ich meine das so was von kein Stück nicht böse, nur sagt es ja wohl keiner, Du verwechselst gewaltig "Erklärung" und "Beschreibung". Wenn wer fragt, warum ist die Ampel rot, dann ist die Aussage, die Ampel ist rot, keine Erklärung.

---

Oder hast Du doch diese "Erklärung" von Dir gemeint:

JosephConrad schrieb am 16.12.2025:

kaktuss schrieb am 16.12.2025:... wieso geht hier die bewegte Atomuhr im Flugzeug langsamer?

Du fliegst sehr schnell von der Erde weg und kommst wieder zurück:

In der Zwischenzeit ist Dein bei der Geburt 30 Jahre jüngerer Sohn genau so alt wie Du. Und es gibt eine Geschwindigkeit, bei der z.B. bei Deiner Rückkehr auf der Erde Milliarden Jahre vergangen sind, obwohl Du nur ein paar Wochen unterwegs warst. Je näher bei c, desto größer der Unterschied.

Ist ja egal was Du nun meinst, beides sind keine Erklärungen. Das sind Beschreibungen, schon lustig, die Frage ist, warum geht die bewegte Uhr im Flugzeug langsamer, und Du "erklärst", die bewegte Uhr geht bewegt langsamer. Ja, wird enorm geholfen haben, sicher.

---

JosephConrad schrieb:Das alles kannst Du negieren, hilft aber nicht weiter. Bitte denk' mal drüber nach.

Ach was, ich nehme es ist wie es ist und bin scheißehrlich, wird wieder Kratzer hinterlassen, zu wenig Watte, zu harte Worte, zu sehr auf den Punkt, macht Euch mal grade, das ist doch kein Puzzle, wer Mountainbike fahren will, der wird auch mal nass.


Bildquelle: https://www.fraenkische-schweiz.com/erleben/aktiv/mountainbiken

Und ja, ich bin ein klein wenig angefressen, aber das sind ganz ehrliche Emotionen, ich bin die Ruhe selbst, mir läuft nun nicht der Geifer aus den Mundwinkeln. Ich bin einfach sehr ehrlich, eventuell ist ja so ein direktes Feedback mal nötig und eventuell rüttelt das den einen oder anderen auch mal aus seinem Dornröschenschlaf ... :D

delta.m schrieb: ... in Gegenrichtung der Bewegung.

Ich muss mal wieder voll böse, gemein und richtig fies sein, damit ich mich gut fühlen kann. ;)

Leute bitte, Bewegung ist relativ, es gibt keine absolute Richtung für eine Bewegung. Ob sie etwas nach links oder rechts bewegt, vor oder zurück, hoch oder runter, ist nur vom Beobachtersystem abhängig. Die Richtung einer Beschleunigung ist hingegen absolut und systemunabhängig.

Das ist so eine einfache Sache, und die ist so elementar, so wichtig, für den einen kann also die Beschleunigung in Richtung der Bewegung sein und für den anderen in Gegenrichtung. Dieselbe Beschleunigung.

Noch mal, Peter hat ein geiles Motorrad, steht auf dem Parkplatz im Nebel und gibt nun Gas, er beschleunigt.

Erika kommt von hinten auf einem frisierten E-Bike daher, durch den Nebel und überholt mit 80 km/h Peter, der gerade erst bei 20 km/h ist.

Und Erika baut ihren Vorsprung aus.

Dann aber hat Peter endlich die 80 km/h erreicht und beschleunigt weiter, er kommt auf 140 km/h und holt nun richtig auf.

Nach kurzer Zeit hat er Erika nicht nur eingeholt, sondern überholt sie und braust davon.

So, alles aus dem Ruhesystem vom Parkplatz beschrieben, erstmal.

Ganz einfache Sätze.

---

Wie schaut es nun für Peter aus?

Er ist beschleunigt, von hinten kommt Erika an, braust an ihm vorbei, wird dann immer langsamer, und dann ändert sich ihre Bewegungsrichtung, sie kommt nun von vorne wieder auf ihn zu. Bis sie ihn erreicht und dann an ihm vorbei nach hinten sich wegbewegt.

Für Peter hat Erika also ihre Bewegungsrichtung geändert. Dabei fährt sie die ganze Zeit konstant 80 km/h.

---

Wie schaut es nun für Erika aus?

Sie ruht auf ihrem Rad, der Parkplatz bewegt sich unter ihr hinweg. Von vorne kommt Peter angerauscht, und bewegt sich an ihr vorbei. Er wird dabei immer langsamer und dann ändert er die Bewegungsrichtung und bewegt sich nun wieder auf sie zu. Dann erreicht er sie und bewegt sich an ihr vorbei. Dabei wird er immer schneller.

---

Peter beschleunigt die ganze Zeit konstant - in allen Systemen in dieselbe Richtung
Erika bewegt sich die ganze Zeit konstant - im Ruhesystem des Parkplatzes.

Die Beschleunigung von Peter ist absolut und system unabhängig.
Die Geschwindigkeit von Erika ist relativ und vom system abhängig.

Und einfach genug? ;)

JosephConrad schrieb:Deine Erklärungen sind wohl nur von den wenigsten zu verstehen

Das liegt aber nicht an seinen Erklärungen sondern an dem komplexen Thema.

nocheinPoet schrieb:Und einfach genug?

Ist für mich als kompletter Laie eine sehr bildhafte und verständliche Erklärung.