Arrakai schrieb:
nocheinPoet schrieb:Unfug, ich habe das hier, wie mit Zitaten nun belegt, mehrfach angesprochen, erklärt, Quellen dazu genannt. Ich habe immer wieder auf die Relativität der Gleichzeitigkeit (RdG) verwiesen. Nebenbei hat das keiner sonst hier getan, gab doch einige "Erklärungen", warum meckerst Du da nicht mal herum? Oder noch besser, erkläre es doch einfach selber mal so richtig gut.
Du hast das mit Zitaten belegt. Aber es steht eben nicht in dem Text, den ich zitiert habe.
Ja und? Ich muss das nicht in jedem Beitrag neu erklären. Nennt sich eine Diskussion, da lesen normal User auch mehr als nur einen Beitrag, wird in der Regel auch erwartet, damit man weiß, um was es genau geht. Und auch ist es nur eine Tatsache, die ich da benenne, ist so wie wenn wer schreibt, Trump, der Präsident der USA, ... muss man nicht schreiben, Trump reicht aus, gewisse Dinge kann man voraussetzten, vor allem, wenn man sie schon über zehn mal explizit angesprochen und auch erklärt hat, in den vorherigen Beiträgen.
Arrakai schrieb:Dort steht einfach nur eine Schlussfolgerung, die falsch ist.
Nein, da steht eine Aussage, die richtig ist, keine Schlussfolgerung. Ich schlussfolgere nicht, die Erde ist keine Scheibe, ich benenne es.
Ganz deutlich, ich bitte Dich hier Deine Tatsachenbehauptung nun anständig zu belegen.
So läuft es hier, und im Gegensatz zu Dir habe ich Dir ja schon belegt, mathematisch, dass meine Aussage richtig ist, und damit Deine, das meine falsch wäre, eben falsch. Und hier wiederholst Du diese Behauptung noch einfach nur mal so, und belegst nichts.
Aber schauen wie es uns das noch einmal genauer an, meine Aussage war:
nocheinPoet schrieb am 27.12.2025:Dann mal was wirklich passiert, das Raumschiff befindet sich erst im Ruhesystem von Erde/Planet, die Gleichzeitigkeit ist also in beiden Systemen gleich.
Was so wirklich normal für jemanden mit Ahnung von Physik eine ganz triviale Sache ist, die nicht extra erklärt werden muss. Du scheinst das aber nicht verstehen zu können, trotzt ausführlicher Erklärungen.
Erstmal nun Deine Antwort:
Arrakai schrieb:Nö. Dafür reicht ein Ruhesystem nicht aus.
Ich zerlege Dir das nun ein weiteres mal, diese Aussage von Dir ist falsch. Denn ich schreibe ja explizit: "
... die Gleichzeitigkeit ist also in beiden Systemen gleich.".
Also einfach mal richtig zählen, ich spreche von zwei Systemen, zwei Ruhesystemen, eines für Erde/Planet, nennen wir es S und eines für das Raumschiff, nennen wir es S'. Okay?
Gut, ist ja auch gar nicht so schwer, beide Systeme haben eine Geschwindigkeit von v = 0 zueinander.
Alleine das reicht aus und jedem mit etwas Ahnung von der SRT und eben der Relativität der Gleichzeitigkeit (RdG) ist klar, ja, dann sind zwei Ereignisse die in S gleichzeitig sind, natürlich auch in S' gleichzeitig, da gibt es nichts zu debattieren.
Du hingegen, willst debattieren, und Du verstehst diese einfache Aussage von mir offenbar wohl nicht.
So schreibst Du dann ja weiter:
Arrakai schrieb:Uhren können im selben Ruhesystem auch desynchronisiert sein, das ist sogar die Regel. Du musst sie schon explizit synchronisieren. Beide befinden sich dann im selben Inertialsystem.
Ich brauche hier für meine Aussage,
nicht eine physische Uhr zum anfassen und synchronisieren.
Ich habe ja zwei Ruhesysteme definiert, S und S', sind Inertialsysteme und damit auch Koordinatensystem. Die haben je nach Aufbau zwei oder mehr Koordinatenachsen, oft ist es x, y aber hier eben x, t. Damit Du es richtig verstehen kannst, ein Punkt in so einem Koordinatensystem hat Koordinatenwerte, bei x, y sind es eben (x, y) Werte, da gibt es keinen Messstab, da wird nie nicht die y-Achse wo an bestimmten Stellen synchronisiert.
Es macht mathematisch keinen Unterschied, ob man nun ein Koordinatensystem mit x, y Achsen hat, und dann Koordinatenwerte für x und y bekommt, für einen Punkt, oder man Achsen für x, t hat. Und t beschreibt hier einfach nur einen Koordinatenwert für die Variable t, welches in diesem Fall die Koordinatenzeit ist.
Die Koordinatenzeit muss ganz sicher nicht synchronisiert werden, das ist ein "Netz", an jedem Punkt im Koordinatensystem klebt fiktiv ein Schild mit (x, t) Wert.
In der Physik, hier in der SRT nennt man so einen Punkt mit Koordinatenwerten auch in der Regel ein Ereignis.
So, die Grundlagen hab ich Dir nun ein wenig erklärt, kommen wir mal zur Gleichzeitigkeit von zwei Ereignissen.
Wir haben zwei Ereignisse:
- \color{#f0e0d0}\mathrm{E_{\hspace{1px}\tiny 1}}: Flugzeug A startet bei \color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 1} = 8\hspace{1px}Uhr\hspace{3px}UTC,\hspace{5px}x_{\hspace{1px}\tiny 1} = 100\hspace{1px}km} - FRA (Frankfurt am Main)
- \color{#f0e0d0}\mathrm{E_{\hspace{1px}\tiny 2}}: Flugzeug B startet bei \color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 2} = 8\hspace{1px}Uhr\hspace{3px}UTC,\hspace{5px}x_{\hspace{1px}\tiny 2} = 220\hspace{1px} km} - HHN (Hahn)
Die x Koordinatenwerte sind hier eh von keiner großen Bedeutung, aber damit es vollständig ist, mal zwei Städte genommen, die ca. 120 km weit voneinander entfernt sind.
Ich denke mal, wir können uns darauf einigen, dass beide Flugzeuge im Ruhesystem S von FRA/HHN gleichzeitig starten?
Sehr schön, nun gibt es echt was cooles in unserer Welt, wir haben eine
koordinierte Weltzeit kurz UTC, hast Du eventuell ja schon mal gehört, dass ist eine Koordinatenzeit.
Dass ist analog zu dem Beispiel mit Erde, Planeten und Raumschiff, wir haben hier auf unserem blauen Planten auch eine echte Koordinatenzeit.
Gleichzeitigkeit in einem Koordinatensystem ist eben so definiert, dass gilt:
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 1} = t_{\hspace{1px}\tiny 2}}Also in unserem Beispiel hier jetzt, mit den beiden Starts der Flugzeuge in S, sind es eben
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 1}} und
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 2}}.
Damit haben wir zwei Ereignisse, die in S gleichzeitig sind. Und was ist nun mit den echten Uhren?
Wir brauchen für die Szene keine echten physikalischen Uhren, die Koordinatenzeit gilt auch ohne echte Uhr, die sie anzeigt. Wir können natürlich Uhren an den Flughäfen haben, die hier UTC oder auch die lokale Ortszeit anzeigen, aber ob die nun da sind, ob die nun richtig gehen, oder nicht, ändert nichts daran, dass beide Flugzeuge in S gleichzeitig starten.
Damit ist also für S die Gleichzeitigkeit von zwei Ereignissen gezeigt und dafür mussten keine echten Uhren synchronisiert werden. Nun kann wer stänkern und sagen, ja ohne echte Uhr, weiß da vor Ort doch keiner, wie spät es ist, er kennt die Koordinatenzeit ja nicht, doch, geht auch ohne Uhr, die kann auch per Radio genannt werden.
Es muss keine echte physikalische Uhr vor Ort sein, die da die Zeit "misst". Es gibt da an jedem Ort die Koordinatenzeit, ob sie angezeigt wird oder nicht. Und man kann hier auch ohne jede Uhr die Gleichzeitigkeit feststellen, man muss nicht mal 8 Uhr wissen, man muss nur in die Mitte zwischen beiden Orten gehen und wenn das jeweilige Flugzeug startet, sendet jeder Flughafen ein Lichtimpuls. Bekommt man nun beide Signale mittig zwischen beiden Flughäfen gleichzeitig, sind beide Flugzeuge auch gleichzeitig gestartet, man braucht keine einzige Uhr, man muss nicht die Uhrzeit wissen.
Gut, nachdem das eben mal geklärt ist, ging meine Aussage ja nun weiter, wenn wir zwei gleichzeitige Ereignisse in S haben, dann sind die auch in S' gleichzeitig, wenn die Geschwindigkeit zwischen S und S' eben v = 0 ist.
Das habe ich Dir nun ausführlich und ganz einfach
hier mathematisch belegt, ich muss das nun nicht noch einmal Dir vorrechnen. Es liegt also an Dir, wenn Du behauptest, meine Aussage sei falsch, dass zu belegen, wird auch Zeit.
So, ich habe noch einen, für die Gleichzeitigkeit spielt es natürlich auch keine Rolle, ob es nun da vor Ort echte physikalische Uhren zum Anfassen gibt, und dass diese auch synchronisiert wurden, dass zu behaupten ist falsch, und Unfug und zeugt davon, dass die Dinge gar nicht im Ansatz richtig verstanden wurden.
Wir könnten zwei Flughäfen nehmen, wie BER (Berlin) UTC+1/+2 und ATH (Athen) UTC+2/+3, der Unterschied bleibt durch die EU-weite synchronisierte Sommerzeit immer bei 1 Stunde. Die Uhren dort auf den beiden Flughäfen, gehen nicht synchron, sie gehen zwar gleichschnell, was schonmal ganz gut ist, sie zeigen aber ständig einen Zeitunterschied von genau 1 h an.
Für die Frage nach der Gleichzeitigkeit, spielt das aber keine Rolle, was hier echte Uhren anzeigen, ist egal, es geht um die Koordinatenzeit, und so ist es auch in dem Beispiel.
So, damit ist noch mal belegt, meine Aussage:
nocheinPoet schrieb am 27.12.2025:Dann mal was wirklich passiert, das Raumschiff befindet sich erst im Ruhesystem von Erde/Planet, die Gleichzeitigkeit ist also in beiden Systemen gleich.
ist absolut richtig, ohne jeden Zweifel.
Deine unbelegte Behauptung dazu:
Arrakai schrieb:Nö. Dafür reicht ein Ruhesystem nicht aus. Uhren können im selben Ruhesystem auch desynchronisiert sein, das ist sogar die Regel. Du musst sie schon explizit synchronisieren. Beide befinden sich dann im selben Inertialsystem.
Ist in mehren Punkten falsch!
Ich brauche keine echten Uhren für meine Aussage, sie müssen auch nicht synchronisiert sein. Und selbst wenn es zwei gebe, befinden sich sich nicht erst - dann - im selben Inertialsystem, wenn sie synchronisiert wurden.
Weißt Du, es gibt hier nun nicht viele Möglichkeiten für Dich, ich dachte ja lange, Du hast Ahnung von Physik, ich habe mich offensichtlich schwer geirrt. Da ich das nun aber wirklich mehrfach und ausführlich belegt habe, dass meine Aussage richtig ist, Deine hingegen wirklich falsch, wäre es doch an der Zeit, dass Du nun Farbe bekennst und einlenkst und Deinen Irrtum zugibst. Eventuell noch eine kleine Entschuldigung, weil Du ein wenig patzig warst, aber das wird wohl nicht kommen.
Ganz im Ernst, wenn man die Physik soweit versteht, die Grundlagen, dann ist hier nun echt Ende im Gelände, war es ja vorher schon. Mit etwas Ehre sollte man dann die Größe finden, hier wirklich einzulenken und nicht weiter gegen Windmühlen kämpfen. Irren kann sich ja jeder mal, ich werde es Dir nicht ewig nachtragen.
Aber wir haben ja leider noch mehr, seltsame Aussagen von Dir.
Arrakai schrieb:nocheinPoet schrieb:Eine Uhr ist nur fiktiv verdinglicht, für die Erklärungen, sie zeigt an einem Ort die Koordinatenzeit an.
Nö. Sie zeigt immer die Eigenzeit an. Und sie ist nicht zwingend fiktiv verdinglicht, sondern i.d.R. auch im Gedankenexperiment ein "Ding", sonst müssten wir bspw. nicht über einen langsamen Uhrentransport für die Synchronisation nachdenken. Mindestens jedoch ist eine Uhr in der SRT ein tatsächlicher physikalischer Prozess wie z.B. eine Schwingungsfrequenz und nicht irgendetwas vollkommen fiktives.
Ich frühstücke Deine Aussagen nun mal in größeren Häppchen ab, das einzeln für jeden falschen Satz zu machen, ist müßig. Fangen wir vorne an, meine Aussage ist wieder richtig, ich habe Dir ja oben Koordinatenzeit nun mal richtig erklärt. Nun erkläre ich Dir dann auch noch was Eigenzeit ist, und wo der Unterschied zur Koordinatenzeit gegeben ist.
Erstmal zeigt eine echte Uhr einfach nur einen Wert an, sofern sie korrekt funktioniert und geeicht ist, das ist die Eigenzeit. Und Eigenzeit ist eine Differenz, eine Differenz zwischen zwei Zeitpunkten, die Uhr zeigt die vergangene Eigenzeit an, wenn sie bei einem Startereignis auf
\color{#f0e0d0}\mathrm{\tau = 0} gestellt wurde. Ob die Koordinatenzeit t an diesem Startereignis ebenfalls 0 ist, spielt dabei keine Rolle.
Eigenzeit (
\color{#f0e0d0}\mathrm{d\tau}), ist die physikalisch gemessene Zeit einer konkreten Uhr entlang ihrer Weltlinie.
Sie ist die Differenz (Integral über
\color{#f0e0d0}\mathrm{d\tau = \sqrt{dt^{\hspace{1px}\tiny 2} - dx^{\hspace{1px}\tiny 2}/c^{\hspace{1px}\tiny 2}}}) zwischen zwei Ereignissen auf der Uhr selbst. Sie ist das, was eine reale, mitreisende Uhr anzeigen kann. Sie ist nicht ohne weiteres übertragbar.
Die Eigenzeit ist die Zeit, die entlang der konkreten Weltlinie der Uhr vergeht. Wenn die Uhr bei einem Ereignis auf
\color{#f0e0d0}\mathrm{\tau = 0} gestellt wird, gibt ihre Anzeige bei einem späteren Ereignis direkt die Eigenzeit zwischen diesen beiden Ereignissen an.
In diesem Sinne zeigt eine Uhr immer Eigenzeit – im Gegensatz zur Koordinatenzeit
\color{#f0e0d0}\mathrm{t}, die sie nur anzeigen würde, wenn sie ruhend und synchronisiert im betreffenden Inertialsystem wäre.
Die Uhr zeigt diesen Wert
\color{#f0e0d0}\mathrm{\Delta \tau} an, wenn sie beim ersten Ereignis auf Null gestellt wurde. Die absolute Anzeige von zum Beispiel 12:00 ist willkürlich, aber
die Änderung der Anzeige zwischen zwei Ereignissen entspricht immer der vergangenen Eigenzeit.
Entscheidend ist, dass die Uhr bei einem Startereignis auf Null gesetzt wird, ob die Koordinatenzeit dort
\color{#f0e0d0}\mathrm{t = 0} ist, spielt für die Eigenzeit keine Rolle.
Noch mal ganz deutlich, eine Uhr kann die Eigenzeit anzeigen, die gleich er Koordinatenzeit ist, dass ist dann der Fall, wenn sie richtig gestartet wurde und im System ruht. Das "ruht" ist entscheidend. Die Uhr auf der Erde ruht wie die Uhr auf dem Planeten in S, die physischen Uhren dort zeigen somit die Koordinatenzeit an und auch die Eigenzeit, was hier eben gleich ist.
Die im System S bewegte Uhr zeigt nur die Eigenzeit an, sie zeigt nicht die Koordinatenzeit im System S an. Sie zeigt recht sicher aber die Koordinatenzeit in S' dem Ruhesystem der Rakete an, denn dort ist das gleich der Eigenzeit. Dafür zeigen die Uhren auf Erde und Planet in S' dem Ruhesystem des Raumschiffs nur die Eigenzeit an, die Koordinatenzeit ist in S' eine andere.
Vertiefen wir das mal weiter:
Wir haben ein Koordinatensystem mit den Achsen x, t und somit für jeden Punkt, also jedes Ereignis, Koordinatenwerte. Ein physische Uhr, eine zum Anfassen wird nicht benötigt, wenn man die Relativität der Gleichzeitigkeit in der Speziellen Relativitätstheorie erklären will. Weniger kann auch manches Mal mehr sein. Oft zeichnet man zwei Koordinatensysteme in ein Diagramm, ein Minkowski-Diagramm, dann gibt es neben den beiden x, t Achsen noch die x' und t' Achse. Oft sieht man hier auch ct und ct' an den Achsen, hier wurde einfach nur mit der Lichtgeschwindigkeit multipliziert, damit man auf beiden Achsen mit Längen arbeiten kann. Die Einheit kann dann Lichtsekunde (Ls) sein.
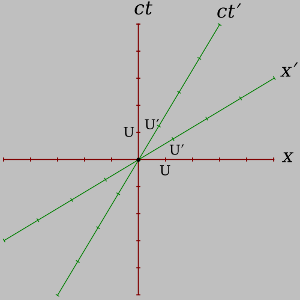
Quelle:
Wikipedia: Minkowski-DiagrammWie man sehen kann, sind die beiden Achsen von S' dem "bewegten" System hier gekippt. Und die Einheiten sind skaliert. Die Einheiten im gestrichenen System sind länger, das ergibt sich aus der Minkowski-Metrik.
So weit so gut. Nun kann man natürlich auch echte physische Uhren als echte Objekte ins Spiel bringen, die sich da eben bewegen, wird oft so gemacht, man stellt eine ins Raumschiff und eine auf die Erde und eine auf den Planeten. Wichtig ist aber das alles auch genau verstanden zu haben, es mag für die Erklärung eventuell von Vorteil sein, es ist aber nicht zwingend nötig, solche Uhren einzubauen.
Wir können in einem System eine ruhende Uhr haben, zum Beispiel auf der Erde und die dann zweimal nacheinander ablesen, und dann die zeitliche Differenz
\color{#f0e0d0}\mathrm{\Delta t} zwischen zwei Ereignissen berechnen. Hier haben wir dann den Fall, dass die Koordinatenzeit in S gleich der Eigenzeit der Uhr ist, welche sie anzeigt. Wenn sie beim Start eben 0 angezeigt hat.
Wir können auch eine bewegte Uhr im System haben, das ist dann eine schräge Linie, eine Weltlinie und auch hier können wir die Differenz zwischen zwei Ereignissen berechnen und bekommen dann die Dauer zwischen zwei Ereignissen in Eigenzeit.
Wichtig, für die Eigenzeit ist es nicht entscheidend, ob die Uhr im System ruht oder sich bewegt, nur, dass es dieselbe Uhr ist, die zweimal abgelesen wird.
Nun kommt der wichtige Teil:
Wir haben nun die im System bewegte Uhr bei zwei Ereignissen abgelesen, die im Raumschiff beim Start und dann bei Ankunft am Planeten, es ist dieselbe Uhr, die Differenz ist die Eigenzeit.
Nun können wir aber noch etwas anders machen, wir schauen auf die Uhr welche in S auf der Erde ruht, beim Start des Raumschiffes und nehmen den Zeitpunkt
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 1} = 0}. Das ist auch die Koordinatenzeit, die physische Uhr vor Ort zeigt die eben auch richtig an.
Dann gehen wir zum Planeten, zu dem Ereignis wo die Rakete beim Planeten ankommt, und wir ja schon die Anzeige der bewegten Uhr in der Rakete abgelesen haben um die Reisedauer für die Rakete in S' zu berechnen. Kurz gesagt, ist das was die Uhr da eben anzeigt, die Eigenzeit.
Aber jetzt schauen wir uns die Koordinatenzeit in S bei diesem Ereignis an, wir suchen hier also
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 2} = 0}.
Und auch hier berechnen wir dann die Reisedauer der Rakete, mit
\color{#f0e0d0}\mathrm{\Delta t = t_{\hspace{1px}\tiny 2} - t_{\hspace{1px}\tiny 1}}.
Ganz wichtig ist nun, wir haben hier zwei verschiedene Uhren in S, welche wir ablesen. Auch wenn es Koordinatenzeit ist, können wir ja auf Erde und Planet nun auch physische Uhren haben, welche die Koordinatenzeit vor Ort richtig anzeigen. Ganz deutlich, wir brauchen sie da nicht, aber um die RdG einfacher erklären zu können, macht es schon Sinn, sie sich da mal zu denken.
Denn so wird klar, wir lesen hier zwei unterschiedliche Uhren ab, was wir an Zeitdifferenz mit
\color{#f0e0d0}\mathrm{\Delta t} bekommen, ist keine Eigenzeit. Aber diese Differenz ist in S dennoch gleich der Eigenzeit auf den Uhren bei Erde und Planet. Der Wert kann gleich sein, aber wirklich Eigenzeit ist es nur, wenn wir beide Mal ein und dieselbe Uhr ablesen. Lesen wie zweimal die Uhr auf der Erde ab, ist es die Eigenzeit. Zweimal auf dem Planeten, auch Eigenzeit. Lesen wir aber einmal Erde und einmal Planet ab und verrechnen das dann, ist das keine Eigenzeit. Auch wenn der Wert hier gleich groß ist.
Leider wird das mit der Eigenzeit sehr oft nicht wirklich richtig verstanden und ja ich habe das echt redundant erklärt. Wenn von acht Erklärungen nur eine fruchtet, wäre das doch schon mal gut.
Und nun die Synchronisation, nur physische Uhren können synchronisiert werden, hier müssen die beiden Uhren auf Erde und Planet also wirklich synchronisiert worden sein, damit man die Reisedauer, den zeitlichen Abstand zwischen beiden Ereignissen in S richtig berechnen kann.
Aber wenn man weiß, wie die Dinge sind, das mit der Koordinatenzeit verstanden hat, weiß was Eigenzeit genau ist, braucht man hier dafür keine physische Uhren, die synchronisiert wurden. Denn durch die Synchronisation zeigen sie eh vor Ort in S die richtige Koordinatenzeit an.
Warum ist das nun so wichtig?
Wenn wir die Dauer zwischen zwei Ereignissen richtig berechnen wollen, brauchen wir vor Ort eine Uhr, irgendwie müssen wir ja auch an die Koordinatenzeit an dem Ort kommen. Damit wir die richtige Zeit bekommen, müssen die beiden Uhren an unterschiedlichen Orten gleichzeitig gleiche Werte anzeigen, sie sind dann synchronisiert.
Entscheidend ist nun, dass in der SRT die Gleichzeitigkeit relativ ist, ich sage ja immer, man muss die Relativität der Gleichzeitigkeit (RdG) richtig verstanden haben, um das mit der Zeitdilatation überhaupt verstehen zu können. Dafür muss man natürlich die Grundlagen davor richtig verstanden haben, was ist ein Koordinatensystem, was nicht, was ein Inertialsystem, was Koordinatenzeit und was ist genau Eigenzeit.
Wenn wir nun die Reisedauer in S berechnet haben, in dem wir die beiden Zeitpunkte Start und Ankunft nehmen, und die Differenz daraus errechnen, können wir das in S ganz einfach mit der Koordinatenzeit machen. Und hier zeigt sich, diese Differenz ist größer, als das was uns die in S bewegte Uhr im Raumschiff an Eigenzeit anzeigt. Diesen Vergleich, das nennt man Zeitdilatation.
Nun kommt aber erst der Knaller, der entscheidende Punkt:
Wir wissen in S, gleiche Anzeige auf Uhren, bedeutet Gleichzeitigkeit, alle Ereignisse mit der Koordinatenzeit t sind gleichzeitig. Wir sagen also, die Uhr auf dem Planeten zeigt gleichzeitig mit der Uhr auf der Erde t = 0 an, wenn das Raumschiff startet. Und dann zählt diese Uhr eben die Reisedauer hoch und wir können auf der anderen Uhr, die auf dem Planteten die Reisdauer in S ablesen.
Das ist aber in einem anderen System S', dass zu dem von Erde/Planet bewegt ist, nicht der Fall. Heißt, wenn sich das Raumschiff bewegt, sind die beiden Zeitpunkte
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 1} = 0} und
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 2} = 0} nicht gleichzeitig. Wir auf der Erde gehen davon aus, ja, die Uhr auf dem Planeten ist mit der auf der Erde synchronisiert, sie zeigen gleichzeitig gleiche Koordinatenzeiten an.
Im Ruhesystem S' vom Raumschiff ist das aber so eben nicht, da starten die beiden Uhren auf Erde und Planet nacheinander. Sie gehen asynchron!
Das ist wichtig, denn der im Raumschiff sagt nun, wenn die Uhr auf der Erde mit t = 0 startet, dann zeigt die auf dem Planten schon etwas an, die ist da schon gestartet. Und nur darum bekommt man eine Reisdauer in S berechnet, die größer als die im Raumschiff ist.
Denn wegen dem Relativitätsprinzip kann der Reisende im Raumschiff zurecht behaupten, er ruht und Erde und Planet sind bewegt, die Uhren dort müssen dilatiert gehen, und weniger Reisezeit messen, während er sieht, wie erst die Erde und dann der Planet an ihm vorbeifliegen.
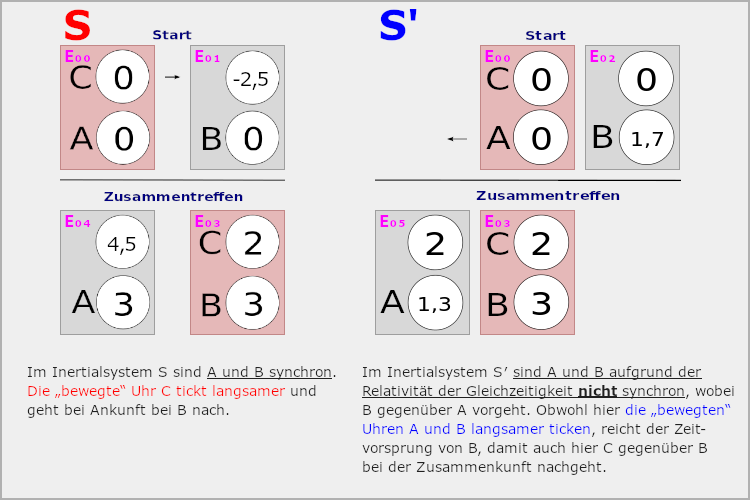
Hier kann man das noch mal gut sein. Und der Reisende hat natürlich recht, für ihn gehen die Uhren auf Erde und Planet als in seinem System bewegte Uhren dilatiert.
Jetzt hab ich doch wieder so viel geschrieben, darum muss ich die Aussage noch mal zitieren:
Arrakai schrieb:nocheinPoet schrieb:Eine Uhr ist nur fiktiv verdinglicht, für die Erklärungen, sie zeigt an einem Ort die Koordinatenzeit an.
Nö. Sie zeigt immer die Eigenzeit an. Und sie ist nicht zwingend fiktiv verdinglicht, sondern i.d.R. auch im Gedankenexperiment ein "Ding", sonst müssten wir bspw. nicht über einen langsamen Uhrentransport für die Synchronisation nachdenken. Mindestens jedoch ist eine Uhr in der SRT ein tatsächlicher physikalischer Prozess wie z.B. eine Schwingungsfrequenz und nicht irgendetwas vollkommen fiktives.
Ich habe Dir ja nun den Unterschied zwischen Eigenzeit und Koordinatenzeit erklärt und aufgezeigt, wir brauchen überhaupt keine physischen Uhren um die RdG zu erklären. Wenn man sie einbaut, sollte das richtig erklärt werden. Ich sprach ja in meiner ersten Aussage, die richtig ist, und die Du fälschlich als falsch bezeichnet, unbelegt, gar nicht von einer Uhr. Ich spreche nur über die Gleichzeitigkeit und beziehe mich hier zurecht implizit auf Koordinatenzeit. Weil man damit feststellt, ob zwei Ereignisse in einem System gleichzeitig sind oder nicht. Ohne jede physikalische Uhr.
Noch mal zur Erinnerung, meine richtige Aussage:
nocheinPoet schrieb am 27.12.2025:Dann mal was wirklich passiert, das Raumschiff befindet sich erst im Ruhesystem von Erde/Planet, die Gleichzeitigkeit ist also in beiden Systemen gleich.
Ich hoffe echt, Dir ist nun endlich klar geworden, dass diese Aussage physikalisch richtig ist, ich habe Dir das nun echt lange und breit erklärt, und
hier auch vorgerechnet und mathematisch bewiesen.
Das Du da mit Uhren kommst, die ja erst synchronisiert sein müssen, ist falsch, geht am Thema auch vorbei.
Arrakai schrieb:nocheinPoet schrieb:Weil vor dem Start \color{#f0e0d0}\mathrm{v=0} ist, hängen \color{#f0e0d0}\mathrm{t'} und \color{#f0e0d0}\mathrm{t} durch \color{#f0e0d0}\mathrm{t' = t} zusammen, daher ist Gleichzeitigkeit in beiden Systemen dieselbe.
Ich habe den Eindruck, dass du da ein grundlegendes Verständnisproblem hast.
Das sagt ja der Richtige, im Gegensatz zu Dir, kann ich aber belegen, dass Du falsche Aussagen machst, die recht sicher auf ein grundlegendes Verständnisproblem beruhen.
;)
Arrakai schrieb:Nehmen wir deine isolierte Aussage, und nur auf genau diese habe ich mich bezogen (und nicht auf das halbe Dutzend anderer Stellen, die du zitiert hast). Und die ist einfach falsch.
ㅤ
Nein, die Aussage ist richtig:
nocheinPoet schrieb am 27.12.2025:Dann mal was wirklich passiert, das Raumschiff befindet sich erst im Ruhesystem von Erde/Planet, die Gleichzeitigkeit ist also in beiden Systemen gleich.
Belege einfach, dass sie falsch ist. Nicht schwurbeln, belegen! Ich weiß, Du kannst es nicht, weil ich Dir bereits mathematisch bewiesen habe, sie ist so richtig. Aber versuche es doch einfach mal, ich bin gespannt.
Weil Du es aber nicht kannst, versuchst Du es nun mit einem Strohmann:
Arrakai schrieb:Zwei Raumschiffe fliegen aufeinander zu, bremsen ab, und befinden sich danach in einem gemeinsamen Ruhesystem. Willst du ernsthaft behaupten, dass deren Uhren plötzlich synchron laufen?
Nichts davon findet sich in meiner Aussage, Du kommst mit einem ganz anderen Beispiel an, eine ganz andere Szene, Du hast nun zwei System und Beschleunigung, und auch noch Uhren, gibt es in meiner Aussage nicht. Keine Bewegung, zwei System S und S' ruhen zueinander, und darum ist die Gleichzeitigkeit in beiden Systemen gleich. Das ist meine Aussage, die ist so richtig.
Ich will Dir aber gerne Deine Frage beantworten, echtes Interesse etwas dazuzulernen soll ja nicht vergeudet sein, wenn wir also eine ganz andere Szene nehmen, zwei zueinander bewegte System, und dann eines beschleunigen, so dass beide zueinander ruhen, dann sind Ereignisse die in dem einen System gleichzeitig sind, auch wieder im anderen gleichzeitig. Das bedeutet aber nicht, dass die Uhren nun in beiden Systemen synchron laufen, also gleichzeitig gleiche Zeiten anzeigen.
Du verwechselst hier etwas wirklich elementares, gleiche Anzeigen auf zwei physischen Uhren bedeuten nicht, dass die beiden Ereignisse dort in dem System auch gleichzeitig sind.
Es geht bei der Frage nach Gleichzeitigkeit um Koordinatenzeit. Und zwei Ereignisse können in S nun bei
\color{#f0e0d0}\mathrm{t_{\hspace{1px}\tiny 1} = t_{\hspace{1px}\tiny 2} = 3\hspace{1px}h} sein, also in S gleichzeitig und in S' kann das
\color{#f0e0d0}\mathrm{t'_{\hspace{1px}\tiny 1} = t'_{\hspace{1px}\tiny 2} = 5\hspace{1px}h} sein. Auch da sind die beiden Ereignisse aber gleichzeitig.
Du kommst hier wirklich mit einem Strohmann und versuchst, mich über den Tisch zu ziehen.
Denn hier spielt auch noch eine ganz andere Sache eine Rolle, also wie üblich die RdG, aber bei Beschleunigung laufen zwei Uhren eben auseinander, je nach Abstand und Größe der Beschleunigung. Dazu kommt, die beiden Uhren sollten ja gleichzeitig beschleunigt werden, der Körper muss star sein, aber die Gleichzeitigkeit verändert sich bei Beschleunigung ständig. Hier könnte man dann mit Rindler-Koordinaten arbeiten.
Aber wie gesagt, dass ist total drüber, recht sicher werden die Uhren aus S nicht mit den Uhren in S' nach der Beschleunigung synchron gehen, alleine nur die Uhren in S', also dem Raumschiff, werden nach dem Abbremsen nicht mehr synchron gehen und gleichzeitig gleiche Zeiten anzeigen.
Da Du aber lernwillig scheinst, erkläre ich es eben noch genauer, vor der Beschleunigung:
S und S' ruhen relativ zueinander → alle Uhren (in S und S') sind synchronisiert. Die Gleichzeitigkeit ist in beiden System gleich, meine Aussage. Ereignisse die in S gleichzeitig sind, sind es auch in S'. Unabhängig ob es da physisch Uhren gibt und ob die synchronisiert wurden.
Während der Beschleunigung von S':
S' ist kein Inertialsystem mehr. Im Raumschiff (S') treten ortsabhängige Zeitdilatationseffekte auf (Rindler-Effekt). Die Uhren an verschiedenen Orten in S' laufen unterschiedlich schnell und sammeln unterschiedliche Eigenzeiten an.
Nach der Beschleunigung (S' ruht wieder relativ zu S):
Uhren in S' sind untereinander asynchron - sie zeigen unterschiedliche Zeiten an und bleiben es. Uhren in S sind weiterhin synchron untereinander, da S während des gesamten Vorgangs ein unbeschleunigtes Inertialsystem blieb. Die Uhren in S' laufen jetzt zwar wieder gleich schnell (da sie im gleichen Inertialsystem ruhen), aber mit konstanten Verschiebungen ihrer Anzeigen.
Hoffe das hilft Dir etwas beim richtigen Verständnis der SRT.
Noch mal nachgeschoben, nun könnte wer sagen, dann ist der hinten in der Rakete nicht genau so gealtert, wie der vorne in der Rakete, während die beschleunigt wurde? Ist dass dann nicht Zeitdilatation durch Beschleunigung?
Ja und nein, ja sind unterschiedlich gealtert, nein es gibt keine Zeitdilatation durch Beschleunigung, dass hier ist auch nur wieder ein Effekt der RdG.
:D
Arrakai schrieb:Aber auch bei deinen konkreten Vorgaben gibt es ein grundlegendes Problem mit deiner Aussage, vor dem Start mag sie korrekt sein.
Na geht doch, hat ja gedauert.
:DJa, meine Aussage ist richtig, und ich sprach ja explizit nur davon, dass S und S' zueinander ruhen, hat das nun so weh getan?
Arrakai schrieb:Aber mit dem Start ist eine Beschleunigung verbunden, wodurch die Uhren sofort desynchronisiert werden. Konstruiere das mal so, dass keine Desynchronisation stattfindet. Bin gespannt.
Aber "aber" ist egal, Du bringst hier wieder Deinen Strohmann, meine Aussage bezog sich ja nicht auf eine Beschleunigung oder auf etwas nach dem Start. Ich beschrieb genau die Stelle in der Szene, die vor dem Start liegt, ich habe nie bestritten, dass die Uhren durch Beschleunigung asynchron werden. Und nicht nur zwischen S und S', auch alleine schon nur in dem System, dass beschleunigt. Auch das hab ich hier im Rahmen des Zwillingsparadoxon aber schon erklärt gehabt.
Dein Versuch, recht billig mit Verlaub, nun zu konstruieren, meine Aussage wäre ja falsch, weil die Uhren bei Beschleunigung ihre Synchronisation verlieren, ist so leicht als Strohmann zu erkennen, und dann noch die Aufforderung, ich solle das mal so konstruieren, dass die Uhren nicht ihre Synchronisation verlieren, und damit zu implizieren, ja also wenn ich das nicht kann, dann ist meine Aussage ja doch falsch.
:DNein, meine Aussage ist richtig, und Du hast es immerhin ja nun auch eingeräumt, kannst es aber nicht ohne "aber" so dann stehen lassen und musst schon wieder daran kratzen.
;)
Arrakai schrieb:nocheinPoet schrieb:Was zu belegen wäre, bisher hast Du Dich zweimal geirrt. Zwei Aussagen von Dir waren einfach falsch, eine habe ich eben ja abgearbeitet, eine gestern und eine hab ich noch gar nicht aufgegriffen.
Alle Aussagen von mir sind richtig.
Klar, und die Erde eine Scheibe.
:D Deine Aussagen sind falsch, nicht alle, aber die, die ich Dir aufgezeigt habe. Falsche Aussagen von mir konntest Du nicht nachweisen, wobei ich nicht sagen will, dass es hier keine geben mag. Aber gefunden hast Du bisher keine.
Arrakai schrieb:nocheinPoet schrieb:Blödsinn, Sehen hat was mit Licht zu tun, wenn also geschrieben wird "von der Erde aus sehen", kommen da oft Lichtlaufzeiten rein, die da echt nichts verloren haben. Da gibt es dann auch Fragen wie, ja aber der Planet ist doch 4 Lj weit weg, dann kann doch keiner was auf der Erde da sehen, also nicht bevor das Licht vom Planeten bis zur Erde geflogen ist.
Gibt es solche Fragen? Man muss sich einfach darauf verständigen, die Lichtlaufzeiten außer Acht zu lassen. Ist hier nach meiner Erinnerung auch so passiert. Davon abgesehen kann der Inertialbeobachter tatsächlich alles sehen, wenn man sich bspw. das Szenario mit den Kameras anschaut. Zwar auch erst dann, wenn ihn die Daten erreichen. Allerdings speichern die Kameras die Timestamps, sodass er nicht mal rechnen muss, sondern einfach ablesen kann.
Ja, kann man machen, muss man aber nicht. Es steht Dir frei, die Dinge so zu erklären, wie Du es für richtig und am einfachsten verständlich hältst, ich halte es ja auch so. Bisher hab ich aber nicht von Dir an Erklärungen gelesen, schon seltsam.
Arrakai schrieb:nocheinPoet schrieb:Nein, dass fragst Du jetzt, nachdem ich Dir aufgezeigt habe, dass meine Aussage richtig ist, und Deine falsch. Nun willst Du das relativieren und im Nachhinein noch eine Frage davor bauen.
Quark. Auch die Linien, die du ins Minkowski-Diagramm zeichnest, werden "Weltlinie" genannt. Mag ungenau sein, ist aber so, und wird sogar in mindestens einer der von dir verlinkten Quellen so gemacht: ...Es [das Minkowski-Diagramm] stellt die Raumzeit in einem Inertialsystem dar, in dem der bisherige gemeinsame Wohnort in Ruhe ist. Er entspricht der (rot dargestellten) Weltlinie des zuhause bleibenden Bruders. Die Weltlinie der Schwester ist in blau eingezeichnet: Im Ereignis A trennt sie sich von ihrem Bruder, fährt zunächst mit Geschwindigkeit v nach rechts, kehrt im Ereignis M um, fährt mit derselben Geschwindigkeit v wieder zurück und trifft im Ereignis B wieder zuhause ein.
Quelle: https://homepage.univie.ac.at/franz.embacher/SRT/Zwillingsparadoxon.html
Und die werden dann halt mit dem Lineal gemessen und es entsteht die exakt umgekehrte Situation wie beim Berechnen von Δτ.
Nein, wenn die Du Länge der Eigenzeit, der Weltlinie richtig ausmessen willst, musst Du im Minkowski-Diagramm mit den Einheiten auf der x' und t' Achse arbeiten, und die sind länger als die Einheiten in S für die x und t Achse. Und wenn Du da dann im richtigen System mit den richtigen Längen auf den richtigen Achsen misst, mit den richtigen Einheiten, dann bekommst Du auch das richtige Ergebnis, eben dass die Eigenzeit, die Weltlinie der im System bewegten Uhr kürzer ist.
Quelle:
Wikipedia: Minkowski-DiagrammAuf der Grafik kann Du das sehr gut erkennen. Du kannst natürlich auch die Koordinatenzeit vom Anfang der Weltlinie und vom Ende in S abgreifen und die Differenz ausrechnen, dann hast Du eben
\color{#f0e0d0}\mathrm{\Delta t} die Reisedauer in S, aber ganz sicher nicht die Eigenzeit und die richtige Länge der Weltlinie.
Und ich habe nie bestritten, dass auch die Erde ruhend in S eine Weltlinie hat, natürlich hat sie die, senkrecht nach oben, eine echte physische Uhr, die dort ruht, würde die Koordinatenzeit anzeigen und auch die Eigenzeit in S, welche sie da eben misst. Habe nie etwas anderes behauptet, im Gegenteil.
Keine Ahnung, ob Du das weißt, oder nun inzwischen weißt, oder noch immer nicht weißt, die Länge der Weltlinie ist die Eigenzeit, die musst Du richtig messen, die Eigenzeit der bewegten Uhr im System S ist aber kürzer, oder kleiner, als der Abstand zwischen den beiden Zeitpunkten, darum zeigt die "Uhr" auf der Erde mehr vergangene Eigenzeit an, als die bewegte Uhr.
Das geht nur, wenn Du die richtigen Einheiten zum Messen nimmst, die auf der t' und x' Achse. Das mit t und x auszumessen macht keinen Sinn. Oder anders, es gibt zumindest nicht die Eigenzeit und die Länge der Weltlinie.
Arrakai schrieb:nocheinPoet schrieb:Wollen wir es einfach mal ganz nett, nur unpräzise nennen. Fakt ist, alle Uhren, ruhend oder bewegt, synchronisiert oder auch nicht, befinden sich im selben Inertialsystem. Dein "dann" nach der Aussage, sie müssten erst synchronisiert werden, impliziert hier, sie würden sich sonst nicht im selben Inertialsystem befinden können. Das ist aber Unfug, wie definieren einfach eine Inertialsystem S und darin "befinden" sich alle Uhren, die ruhenden, die bewegten, die synchronisierten und die nicht synchronisierten. Ist doch gar keine Problem.
Alles kann mit allen Koordinatensystemen beschrieben werden, das ist korrekt, sonst wären sie ja nicht gleichberechtigt.
Ja, ich stimme doch gerne zu.
Arrakai schrieb:Ein Inertialsystem wird allerdings durch Körper aufgespannt, die zueinander ruhen und deren Uhren synchron laufen. Alles, was diese Bedingung nicht erfüllt, befindet sich nicht in dem Inertialsystem. Mir ist diese Formulierung genau genug.
Wenn Dir das genug ist, erklärt das einiges, auch warum ich der Meinung bin, Du solltest anderen nicht die SRT und die RdG versuchen zu erklären, solange Du die Dinge nicht richtig verstanden hast.
;)Die "Probleme" und "Unschärfen" in Deiner Aussage:
- "... durch Körper aufgespannt": Ein Inertialsystem ist ein abstraktes Koordinatensystem (t, x, y, z), das die Raumzeit beschreibt. Es wird nicht zwingend durch physische Körper definiert – diese können lediglich als „Marker“ dienen.
- "... befindet sich nicht in dem Inertialsystem": Diese Formulierung ist irreführend. Ein bewegter Körper ist sehr wohl im selben Inertialsystem beschreibbar, nur hat er dann eine zeitlich veränderliche Ortskoordinate. Gemeint ist wohl: „gehört nicht zum ruhenden Bezugskörper, der das System repräsentiert“.
- Fehlende Dynamik: Die Definition eines Inertialsystems beinhaltet essenziell, dass sich kräftefreie Körper darin geradlinig gleichförmig bewegen - nicht nur, dass einige Körper ruhen. Diese zentrale Eigenschaft wird nicht erwähnt.
Ein Inertialsystem lässt sich durch ein Netzwerk von ruhenden, zueinander synchronisierten Uhren und Maßstäben denken. Alle Körper, die relativ zu diesem Netzwerk ruhen, gehören zum selben Ruhesystem. Körper, die sich relativ dazu bewegen, können trotzdem mit den Koordinaten des Inertialsystems beschrieben werden. Entscheidend ist, dass in einem Inertialsystem kräftefreie Körper geradlinig gleichförmig bewegt erscheinen.
Oder so ähnlich, geht sicher kürzer und eventuell auch noch besser.
