Eine Frage zu Einstein und seiner Relativitätstheorie

JosephConrad schrieb:Die Uhr mit der kürzeren Eigenzeit zeigt weniger verstrichene Zeit an. Längere Weltlinie (gekrümmt, beschleunigt) hat die kürzere Eigenzeit.

Nein, das ist einfach falsch.


In der speziellen Relativitätstheorie gilt für Eigenzeit und raumzeitliche Bogenlänge:

\color{#f0e0d0}\mathrm{Eigenzeit\hspace{5px} \tau = \int d\tau = \int \sqrt{1 - \frac{v^{\tiny 2}}{c^{\tiny 2}}}\hspace{2px} dt}

Dieses Integral ist die Länge der Weltlinie in der Raumzeit (Minkowski-Länge) → Mehr Eigenzeit bedeutet eine längere raumzeitliche Weltlinie

Also, kürzere Weltlinie, weniger Eigenzeit. Ich habe das so nicht definiert, ich gebe es nur richtig wieder. ;)

---

JosephConrad schrieb:
Zwei Ereignisse (Start und Wiedervereinigung):

• Uhr A: bewegt sich gleichförmig (keine Beschleunigung) → gerade Weltlinie
• Uhr B: beschleunigt, kehrt um, ändert Geschwindigkeit → gekrümmte Weltlinie

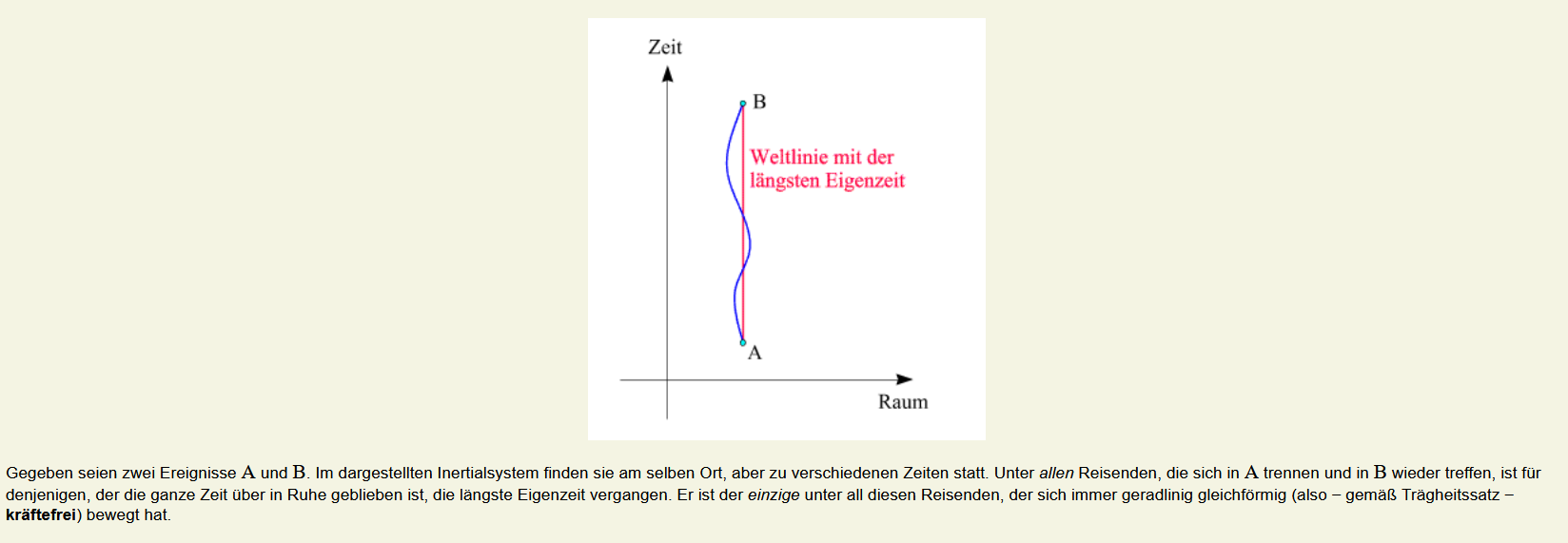
Die gerade (inertiale) Weltlinie hat die größte Eigenzeit. Jede andere, gekrümmte Weltlinie hat weniger Eigenzeit.

Ja.

---

JosephConrad schrieb:Die Uhr mit der längeren (gekrümmten) Weltlinie zeigt weniger Zeit an.

Nein, die Länge der Weltlinie ist fest definiert, habe ich nun mehrfach erklärt. Man kann den Minkowski-Raum eh nicht richtig euklidische abbilden, stelle es Dir wie Perspektive vor.

Schau mal, wenn Peter nur 1 m weit von Dir weg steht und 100 m weiter weg ein Baum mit 20 m Höhe, dann mag das für Dich (auf einem Foto) so ausschauen, dass Peter größer als der Baum ist. Kannst Du nachmessen auf dem Foto. Aber Peter ist nicht größer, weil "Größe" eben nicht so definiert ist, dass man ein Foto macht und die Entfernung unter den Tisch fallen lässt.

Bei dem Beispiel ist die Metrik aber euklidisch, aber Du hast immerhin die Perspektive. Bei der SRT und der Minkowski-Metrik ist das ähnlich, die Linie für den Reisenden mag für Dich länger ausschauen oder mit Lineal gemessen auch sein, aber die Weltlinie ist deswegen nicht länger als die vom nicht reisenden Zwilling.

---

JosephConrad schrieb:

Arrakai schrieb:auf der Uhr mit der längeren Weltlinie wird "weniger [Zeit] anzeigt", nicht auf der mit der kürzeren.

Also stimmt das. Beide Uhren haben schließlich denselben Start- und Endpunkt.

Nein es stimmt nicht. Nehmt mich doch mal aus der Gleichung raus, ich habe verstanden, Ihr hättet gerne einfach, dass ich irre, falsch liege, aber dafür muss man nicht die Physik kaputt machen. Ich irre mich genug, kommt vor, wenn ich was finde, sage ich es Euch, dann könnt Ihr Euch freuen, dass ich mal Unrecht habe.

---

Ganz deutlich:

Die Minkowski-Länge der Weltlinie (die in der Eigenzeit gemessen wird) ist beim Reisenden kürzer als beim ruhenden Zwilling. Auf einem Diagramm mit üblichen Achsen kann die gezeichnete Linie des Reisenden zwar länger aussehen, aber das liegt an der nicht-euklidischen Metrik – ähnlich wie perspektivische Verzerrung auf einem Foto. Entscheidend ist die Eigenzeit, je kürzer die Minkowski-Weltlinie, desto weniger Zeit zeigt die Uhr an.


Die Definition ist entscheidend:

"Länge einer Weltlinie" ist in der SRT per Definition gleich ihrer Eigenzeit (Minkowski-Bogenlänge).

nocheinPoet schrieb:Nein, die Länge der Weltlinie ist fest definiert, habe ich nun mehrfach erklärt

Hier war ja zur Anschauung umgangssprachlich die Länge aus der Zeichnung gemeint, die in einem Diagramm stärker geknickte / "weiter aussehende" Linie
nicht die echte, physikalische Länge.

Auch hier (Universität Wien):




Q:https://homepage.univie.ac.at/franz.embacher/SRT/Zwillingsparadoxon.html

Die grafische Länge ist nicht die Minkowski-Länge, denn bei rot steht ja: die längste Eigenzeit. Aber nur so ist es intuitiv zu verstehen.

JosephConrad schrieb:Aber nur so ist es intuitiv zu verstehen.

Ja, das ist schön verständlich - zumindest für mich :)
aber wahrscheinlich auch wieder "falsch" :(

JosephConrad schrieb:

nocheinPoet schrieb:Nein, die Länge der Weltlinie ist fest definiert, habe ich nun mehrfach erklärt.

Hier war ja zur Anschauung umgangssprachlich die Länge aus der Zeichnung gemeint, die in einem Diagramm stärker geknickte / "weiter aussehende" Linie nicht die echte, physikalische Länge.

Das macht keinen Sinn, erstmal hatte ich eine Aussage gemacht, die hier ja von @Arrakai fälschlicher Weise als falsch bezeichnet wurde. Ich habe belegt, meine Aussage ist richtig. Dann wurde versucht hier Rumzueiern, was aber auch nichts gebracht hat. Dann kommst Du nun in diesem Kontext, uns sprichst von Länge, und widersprichst meiner Aussage, zitierst die von Arrakai und stimmst der zu.

Nein, es ist und bleibt falsch, das ist Physik, die Dinge sind definiert, Peter ist auch nicht größer als der Baum. Der Baum ist nur weiter weg, so wie Du es formuliert hast, und in Anbetracht, dass Du dann noch die Aussage zitierst, ist Deine Aussage falsch. Länge der Weltlinie ist definiert, so wie Größe. Wenn wer sagt, Peter ist größer als der Baum, geht jeder normal Mensch davon aus, dass der Baum wirklich kleiner als Peter ist, und eben nicht, dass das nur auf dem Foto so ausschaut.

Was soll das auch, die echte Länge war nicht gemeint, es gibt nur die echte Länge und die ist definiert wie sie definiert ist.

---

JosephConrad schrieb:
Auch hier (Universität Wien):

https://homepage.univie.ac.at/franz.embacher/SRT/Zwillingsparadoxon.html

Ich kenne die Seite und die ist gut, und die Länge der Weltlinie in rot ist größer. Das ergibt sich so aus der Definition.

---

JosephConrad schrieb:Die grafische Länge ist nicht die Minkowski-Länge, denn bei rot steht ja: die längste Eigenzeit. Aber nur so ist es intuitiv zu verstehen.

Gut, nennen wir es die grafische Länge, die grafische Länge ist aber nicht die Länger der Weltlinie im Rahmen der Definition in der SRT.


Darum ging es, meine Aussage war:

nocheinPoet schrieb am 28.12.2025:Das ist etwas anderes, sie hat eine kürzere Weltlinie, sie hat weniger Strecke durch die Raumzeit gemacht, die Strecke ist kürzer, darum zeigt sie weniger an.

Das wurde zitiert und darauf wurde geantwortet:

Arrakai schrieb:Grundsätzlich: Auf der Uhr mit der längeren Weltlinie wird "weniger [Zeit] anzeigt", nicht auf der mit der kürzeren. Aber ggf. ist mir der Kontext nicht ganz klar?

Und diese Antwort ist falsch.

Wenn da stehen würde, ja die "grafische" Länge in der Grafik, die ist doch aber länger, dann wäre das etwas anderes, steht da aber nicht. Geht um Länge und Weltlinie, damit ist meine Aussage richtig und die andere falsch. Ich habe es belegt, lasst es doch einfach nun gut sein. Ist doch echt nur noch albern.

---

delta.m schrieb:Ja, das ist schön verständlich - zumindest für mich.

Keine Ahnung, was da so für Dich nun verständlich ist, die Minkowski-Metrik ist nicht wirklich zu greifen, da sie unser euklidischen Metrik widerspricht. Es macht doch auch keinen Sinn, die Dinge falsch zu lernen.

delta.m schrieb:Ja, das ist schön verständlich - zumindest für mich :)
aber wahrscheinlich auch wieder "falsch" :(

Manchmal bringt uns das Falschere der Wahrheit näher ...

@JosephConrad

Das ist hier nicht Philosophie oder Esoterik oder Religion, wie soll das falsche der Wahrheit näher sein? Soll das jetzt nur noch Geschwurbel werden? Weil es nicht passt, wie es eben ist?

Die Vorstellung, die Weltlinie ist länger, führt in die Irre, das geht doch auch gar nicht von den Gleichungen. Aber klar, wenn man auf die Gleichungen scheißt, alles egal ist, dann hilft Pipi Langstrumpfs Devise ...

"Hey, Pippi Langstrumpf" Original Soundtrack zum Mitsingen

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

:D

nocheinPoet schrieb:Die Vorstellung, die Weltlinie ist länger, führt in die Irre

Sie ist doch ein Umweg.

nocheinPoet schrieb am 20.12.2025:Es führt dazu, dass "Umwege" in der Raumzeit (Bewegung mit v > 0) zu kürzerer Eigenzeit führen, im Gegensatz zur euklidischen Geometrie, wo Umwege länger sind. Die euklidische Hypotenuse (10) ist analog zur Koordinatenzeit dt, die adjazente Seite (≈8,66) zur Eigenzeit-Komponente und die gegenüberliegende (5) zur Raumkomponente - aber mit umgekehrtem Vorzeichen.

Ach ja: auch Pipi Langstrumpf hat ganze Generationen der Wirklichkeit näher gebracht, gerade wil bei ihr 2 x 3 = 4 war.

@JosephConrad

Keine Ahnung, was Du willst, Du zitierst eine Aussage von mir, die so richtig ist. Ich kann nichts dafür, wenn Du das so nicht packst, ich habe Dir das mit der Analogie Baum und Peter auf dem Foto erklärt. Der "Umweg" macht die Länge im Minkowski-Raum kürzer und nicht länger, so ist eben die Metrik dieses Raumes. Darum heißt er auch nicht euklidischer Raum, weil da der Umweg die Länge auch eben länger macht.

Gibt Dinge, die lernt man erstmal und nimmt sie als gegeben hin und dann kann man immer noch darüber philosophieren. Hier ist es eben nun mal so, Umwege machen die Länge kürzer, klingt seltsam, ist aber so.

nocheinPoet schrieb:Gibt Dinge, die lernt man erstmal und nimmt sie als gegeben hin und dann kann man immer noch darüber philosophieren. Hier ist es eben nun mal so, Umwege machen die Länge kürzer, klingt seltsam, ist aber so.

Sag ich doch, die längere Linie in der Zeichnung hat die kürzere Eigenzeit. Das im euklidischen "Längere" ist hier eben intiutiv.

JosephConrad schrieb:

nocheinPoet schrieb:Gibt Dinge, die lernt man erstmal und nimmt sie als gegeben hin und dann kann man immer noch darüber philosophieren. Hier ist es eben nun mal so, Umwege machen die Länge kürzer, klingt seltsam, ist aber so.

Sag ich doch, die längere Linie in der Zeichnung hat die kürzere Eigenzeit.

Nein, sagst Du, ist aber falsch, und ich sage genau das nicht. Mich zu zitieren und dann zu schreiben, ja genau das sagst Du doch auch so, ist nur noch trollen.

Ich sage, die kürzere Weltlinie hat auch die geringere Eigenzeit. Das war meine Aussage, die war richtig.

Und es bringt nichts zu schwurbeln, ja aber wenn ich die ausmesse, dann ist die grafische Länge aber länger, dass macht so viel Sinn wie zu sagen, ja aber wenn ich Peter auf dem Foto ausmesse, ist er größer als der Baum. Ist er nicht, es geht um Physik. Das also nun grafisch auszumessen, oder hier nun noch eine "grafische" Länge einzubringen, ist destruktiv, dass erklärt nichts, sondern macht es im Gegenteil unverständlicher.

Es soll ja gerade begriffen werden, dass es einen elementaren Unterschied in der Metrik gibt, dass die Minkowski-Metrik eben sich genau in dem Punkt unterscheidet von der euklidischen Metrik.

Eine Minkowski-Länge nun euklidisch auszumessen, ist so sinnvoll, wie eine Strecke in Litern zu messen. :D

nocheinPoet schrieb:Ich sage, die kürzere Weltlinie hat auch die geringere Eigenzeit. Das war meine Aussage, die war richtig.

Nein, Du sagst Umwege machen die Länge kürzer. Einen Umweg kannst Du grafisch nur durch eine längere krumme Linie, o.ä. ausdrücken. Deshalb werden die Zeichnungen ja auch so so gemacht. Dann wird erklärt, dass die Summe der Minkowski-Längen dieser Linien dennoch kürzer ist, als die der geraden Weltlinie, da es sich um raumzeitliche Linien handelt. Alles verständlich. Wenn Du es nicht stehen lassen kannst, dann versuche mit Deiner Art der Pädagogik die Welt zu erklären.

JosephConrad schrieb:

nocheinPoet schrieb:Ich sage, die kürzere Weltlinie hat auch die geringere Eigenzeit. Das war meine Aussage, die war richtig.

Nein, Du sagst Umwege machen die Länge kürzer.

Doch, ich sage beides, soll ich Dir das zigmal zitieren? Der Umweg macht die Länge kürzer, die der Weltlinie. Also hat die kürzere Weltlinie die geringere Eigenzeit. Soll ich es Dir vor jodeln? :D

---

JosephConrad schrieb:Einen Umweg kannst Du grafisch nur durch eine längere krumme Linie, o.ä. ausdrücken. Deshalb werden die Zeichnungen ja auch so so gemacht.

Falsch, das gilt so nur für einen euklidischen Raum, also eine euklidische Metrik. Noch mal, Du verwechselst hier Perspektive mit Physik. Du kommst mit "es sieht doch aber so aus ...", irrelevant, kann man ansprechen, ist aber so wie Du es formulierst dann falsch.

Es gibt auch keinen Sinn, dass ist so sinnvoll wie zu sagen, ja auf dem Foto sieht Peter aber größer als der Baum aus. Ja, ist so, kann sogar so gemessen werden, ist aber physikalisch irrelevant. Denn physikalisch ist Peter nicht größer als der Baum, also bringt so eine Aussage genau nichts.

---

JosephConrad schrieb:Dann wird erklärt, dass die Summe der Minkowski-Längen dieser Linien dennoch kürzer ist, als die der geraden Weltlinie, da es sich um eine raumzeitliche Linie handelt. Alles verständlich. Wenn Du es nicht stehen lassen kannst, dann versuche mit Deiner Art der Pädagogik die Welt zu erklären.

Unfug, ich hatte eine richtige Aussage gemacht, die wurde als falsch bezeichnet und dann wurde eine falsche Aussage gemacht. Ich habe belegt, meine Aussage ist richtig, die andere falsch. Dass hat Dir nicht geschmeckt und Du musst Dich nun einfach einmischen, und weil ich auch Dir auf den Sack gehe, springst Du nun einfach dem anderen zur Seite.

Wenn die Aussage gewesen wäre, also mir gegenüber, ja die Weltlinie mit der geringeren Eigenzeit ist kürzer als die mit mehr Eigenzeit, weil sich das so aus der Minkowski-Metrik ergibt, aber wenn man es so als Grafik sieht, dann schaut die kürzere Weltlinie doch immer länger als die längere Weltlinie aus. Oder so was in der Richtung, hätte ich dem zugestimmt.

Es ist ja so, und ich habe auch schon eingeräumt, ich hätte darauf ruhig mal hinweisen können.

Und es geht hier um Physik, nicht Pädagogik, aber inzwischen wird das eh mehr ein soziales Experiment. :D

nocheinPoet schrieb:Und es geht hier um Physik, nicht Pädagogik, aber inzwischen wird das eh mehr ein soziales Experiment.

Ich belasse den Aspekt jetzt hier. Deine Erklärungen erinnern mich aber oft daran:

JosephConrad schrieb:Ich belasse den Aspekt jetzt hier. Deine Erklärungen erinnern mich aber oft daran: ...

Klar, wer sachlich argumentativ nicht punkten kann, der geht eben ad hominem, ich sage ja, es wird ein soziales Experiment. Du kannst einfach nicht damit umgehen, dass ich widerspreche und das immer und immer wieder. Ist ja auch echt böse und gemein von mir, und da Du nun sachlich gar nichts liefern kannst, muss Du versuchen mich anders zu diskreditieren, und wenn es nur mit einem Meme ist. :D

Das sagt mehr über Dich, als über mich aus. Denn mir ist es egal, was Du glaubst, über Physik und auch über mich, ich schreibe zur Sache und habe die Dinge nur richtig physikalisch widergegeben, aber vermutlich, weil ich eben ich bin, und es da dann doch noch den Faktor der Sympathie gibt, kann man das so nicht hinnehmen, da muss einfach gegengehalten werden.

Und nebenbei, ich habe nur einen Realschulabschluss, da ist nicht mal ein Abitur in der Tasche. :D

nocheinPoet schrieb:Und nebenbei, ich habe nur einen Realschulabschluss, da ist nicht mal ein Abitur in der Tasche. :D

Aber immerhin bist Du auch noch der Bruder vom lieben Gott: "der liebe Gott weiss alles, sein Bruder weiss alles besser." ;)

@JosephConrad

Ach was, ich bin sicherlich eigen, pedantisch, gehe anderen schnell auf die Nüsse, wirke arrogant und wie ein ätzender Klugscheißer. Ist so, Mimik ist schwer schriftlich zu vermitteln, ich krieche nicht, halte nicht mein Maul, und dann gibt es eben was drauf. Ich kann Dir aber sagen, ich sehe das alles ganz locker, ich sitze hier nicht mit Schaume vor dem Mund und der Geifer tropft aus dem Mundwinkel.

Es ist schade, dass hier das nicht mehr so auf der Sachebene geht, wie früher in diesem Bereich. Ist aber eben wohl die TikTok Generation, die Zeiten ändern sich. Früher war Physik für mehr User interessant, heute ist es recht Banane. Kann ich mit leben, ist eben wie es ist. ;)

nocheinPoet schrieb:Es ist schade, dass hier das nicht mehr so auf der Sachebene geht, wie früher in diesem Bereich. Ist aber eben wohl die TikTok Generation, die Zeiten ändern sich. Früher war Physik für mehr User interessant, heute ist es recht Banane. Kann ich mit leben, ist eben wie es ist. ;)

Sei doch nicht gleich so fatalistisch, du weisst doch alles recht gut, was ich kritisierte war ja nur das, was Du selbst geschrieben hast (eigen, pedantisch, anderen schnell auf die Nüsse, arrogant, ätzender Klugscheißer) und noch nicht einmal in dieser Intensität. Beleidigen will ich Dich pers. jedenfalls nicht. Ich bin vielleicht älter als Du.

Die Ursprungfrage war ja:

kaktuss schrieb am 11.12.2025:Eine bewegte Uhr geht langsamer als eine unbewegte.
Für eine bewegte Person vergeht die Zeit langsamer relativ zu einer unbewegten Person.
Die bewegte Person nimmt die Zeit aber normal schnell wahr, friert also nicht ein...
Nun die Uhr aus Satz 1 oben friert aber ein, also geht wirklich langsamer.

Kann mir das bitte mal jemand erklären ?

Aber irgendwie ist hier im Thread fast niemand mehr übrig. Und verstehe das bitte nicht falsch: vielleicht braucht es ja nur ein wenig Fuzzy-Logik statt binärer Logik?

nocheinPoet schrieb:Unfug, ich habe das hier, wie mit Zitaten nun belegt, mehrfach angesprochen, erklärt, Quellen dazu genannt. Ich habe immer wieder auf die Relativität der Gleichzeitigkeit (RdG) verwiesen. Nebenbei hat das keiner sonst hier getan, gab doch einige "Erklärungen", warum meckerst Du da nicht mal herum? Oder noch besser, erkläre es doch einfach selber mal so richtig gut.

Du hast das mit Zitaten belegt. Aber es steht eben nicht in dem Text, den ich zitiert habe. Dort steht einfach nur eine Schlussfolgerung, die falsch ist.

nocheinPoet schrieb:Eine Uhr ist nur fiktiv verdinglicht, für die Erklärungen, sie zeigt an einem Ort die Koordinatenzeit an

Nö. Sie zeigt immer die Eigenzeit an. Und sie ist nicht zwingend fiktiv verdinglicht, sondern i.d.R. auch im Gedankenexperiment ein "Ding", sonst müssten wir bspw. nicht über einen langsamen Uhrentransport für die Synchronisation nachdenken. Mindestens jedoch ist eine Uhr in der SRT ein tatsächlicher physikalischer Prozess wie z.B. eine Schwingungsfrequenz und nicht irgendetwas vollkommen fiktives.

nocheinPoet schrieb:Weil vor dem Start v=0\color{#f0e0d0}\mathrm{v = 0}v=0 ist, hängen t′\color{#f0e0d0}\mathrm{t'}t′ und t\color{#f0e0d0}\mathrm{t}t durch t′=t\color{#f0e0d0}\mathrm{t' = t}t′=t zusammen, daher ist Gleichzeitigkeit in beiden Systemen dieselbe.

Ich habe den Eindruck, dass du da ein grundlegendes Verständnisproblem hast. Nehmen wir deine isolierte Aussage, und nur auf genau diese habe ich mich bezogen (und nicht auf das halbe Dutzend anderer Stellen, die du zitiert hast). Und die ist einfach falsch. Zwei Raumschiffe fliegen aufeinander zu, bremsen ab, und befinden sich danach in einem gemeinsamen Ruhesystem. Willst du ernstaft behaupten, dass deren Uhren plötzlich synchron laufen?

Aber auch bei deinen konkreten Vorgaben gibt es ein grundlegendes Problem mit deiner Aussage: Vor dem Start mag sie korrekt sein. Aber mit dem Start ist eine Beschleunigung verbunden, wodurch die Uhren sofort desynchronisiert werden. Konstruiere das mal so, dass keine Desynchronisation stattfindet. Bin gespannt.

nocheinPoet schrieb:Was zu belegen wäre, bisher hast Du Dich zweimal geirrt. Zwei Aussagen von Dir waren einfach falsch, eine habe ich eben ja abgearbeitet, eine gestern und eine hab ich noch gar nicht aufgegriffen.

Alle Aussagen von mir sind richtig.

nocheinPoet schrieb:Blödsinn, Sehen hat was mit Licht zu tun, wenn also geschrieben wird "von der Erde aus sehen", kommen da oft Lichtlaufzeiten rein, die da echt nichts verloren haben. Da gibt es dann auch Fragen wie, ja aber der Planet ist doch 4 Lj weit weg, dann kann doch keiner was auf der Erde da sehen, also nicht bevor das Licht vom Planeten bis zur Erde geflogen ist.

Gibt es solche Fragen? Man muss sich einfach darauf verständigen, die Lichtlaufzeiten außer Acht zu lassen. Ist hier nach meiner Erinnerung auch so passiert. Davon abgesehen kann der Inertialbeobachter tatsächlich alles sehen, wenn man sich bspw. das Szenario mit den Kameras anschaut. Zwar auch erst dann, wenn ihn die Daten erreichen. Allerdings speichern die Kameras die Timestamps, sodass er nicht mal rechnen muss, sondern einfach ablesen kann.

nocheinPoet schrieb:Nein, dass fragst Du jetzt, nachdem ich Dir aufgezeigt habe, dass meine Aussage richtig ist, und Deine falsch. Nun willst Du das relativieren und im Nachhinein noch eine Frage davor bauen.

Quark. Auch die Linien, die du ins Minkowski-Diagramm zeichnest, werden "Weltlinie" genannt. Mag ungenau sein, ist aber so, und wird sogar in mindestens einer der von dir verlinkten Quellen so gemacht:

Es [das Minkowski-Diagramm] stellt die Raumzeit in einem Inertialsystem dar, in dem der bisherige gemeinsame Wohnort in Ruhe ist. Er entspricht der (rot dargestellten) Weltlinie des zuhause bleibenden Bruders. Die Weltlinie der Schwester ist in blau eingezeichnet: Im Ereignis A trennt sie sich von ihrem Bruder, fährt zunächst mit Geschwindigkeit v nach rechts, kehrt im Ereignis M um, fährt mit derselben Geschwindigkeit v wieder zurück und trifft im Ereignis B wieder zuhause ein.

Quelle: https://homepage.univie.ac.at/franz.embacher/SRT/Zwillingsparadoxon.html

Und die werden dann halt mit dem Lineal gemessen und es entsteht die exakt umgekehrte Sitution wie beim Berechnen von Δτ.

nocheinPoet schrieb:Wollen wir es einfach mal ganz nett, nur unpräzise nennen. Fakt ist, alle Uhren, ruhend oder bewegt, synchronisiert oder auch nicht, befinden sich im selben Inertialsystem. Dein "dann" nach der Aussage, sie müssten erst synchronisiert werden, impliziert hier, sie würden sich sonst nicht im selben Inertialsystem befinden können. Das ist aber Unfug, wie definieren einfach eine Inertialsystem S und darin "befinden" sich alle Uhren, die ruhenden, die bewegten, die synchronisierten und die nicht synchronisierten. Ist doch gar keine Problem.

Alles kann mit allen Koordinatensystemen beschrieben werden, das ist korrekt, sonst wären sie ja nicht gleichberechtigt. Ein Inertialsystem wird allerdings durch Körper aufgespannt, die zueinander ruhen und deren Uhren synchron laufen. Alles, was diese Bedigung nicht erfüllt, befindet sich nicht in dem Inertialsystem. Mir ist diese Formulierung genau genug.

JosephConrad schrieb:Aber irgendwie ist hier im Thread fast niemand mehr übrig.

Also ich lese nach wie vor interessiert mit. Großes Kino.
Für mich die Erkenntnis das das was ich 50 Jahre über das Thema zu wissen glaubte eine Geschichte von der Sorte war die Terry Pratchett mal "Lügen für Kinder" genannt hat. Vereinfacht bis zum Gehtnichtmehr und wichtige Fakten weggelassen. Aber der einzige Weg sich dem Thema zu nähern und das Problem zu verstehen ohne sich mit einer Geometrie zu befassen wo Umwege kürzer sind. Und deshalb die Pippi-Langstrumpf-Rechnung plötzlich stimmt.
Und die Erkenntnis das auch "Wahrheit" über die hier erbittert gestritten wird ähnlich wie die Zeit verd.. relativ sein kann.
Und noch was: Ich hatte vor einiger Zeit hier mal gefragt was den eigentlich für die Zeitverkürzung verantwortlich ist:
Geschwindigkeit
Beschleunigung
Gravitation
Ein Zusammenwirken der obengenannten Faktoren oder
Was ganz anderes
In Wiki-Artikel über das Zwillingsparadoxon meint man: "Die Geschwindigkeit und die Dauer der Reise"

Wikipedia: Zwillingsparadoxon

Zwischendurch hat man sich aber auch "Was ganz anderes" einfallen lassen:
"ist für den reisenden Zwilling die zurückgelegte Strecke kürzer als die Strecke, die der daheimgebliebene Zwilling in seinem Bezugssystem beobachtet."

Ich nehme mal an dass das der "kürzere Umweg" ist über den in dieser Diskussion heute diskutiert wurde.
Was stimmt den nun?
Kann man sagen das durch den Flug mit relativistischer Geschwindigkeit sich die Strecke verkürzt oder ist das eine neue "Lüge für Kinder".