Existiert eine Erklärung für das Noether-Theorem,
die keine Kopfschmerzen bereitet? Alle einfachen Beschreibungen, die man im Internet findet, auch das von mir weiter oben, bleiben weitgehend auf dem Level von Hamilton und Lagrange aus dem 19. Jahrhundert. Wenn man Bewegungsgleichungen so umformen kann, dass absolute Koordiantenangaben nicht nötig sind, dann kann man dadurch die elementaren Erhaltungsgrößen herleiten. Sobald man es aber etwas genauer wissen will, landet man gleich bei Eichsymmetrien und Quantenfeldgleichungen mit einem mathematischen Overkill. Schauder.
Es gibt irgendwo dazwischen allerdings auch eine sehr anschauliche Darstellung für den Kern des Noether-Theorems, also für genau den Zusammenhang zwischen Translationssymmetrien und Erhaltungsgrößen, der von Emmy Noether 1918 mathematisch begründet wurde. Es handelt sich um den "picture proof" von Richard Feynman, siehe erstes Bild. Es findet sich in dem Link auf Seite 105, wobei man die vorhergehenden Kapitel über die Symmetrien ebenfalls gelesen haben sollte. Es ist alles relativ einfaches, gut verständliches Englisch ->
https://www.ling.upenn.edu/~kroch/courses/lx550/readings/feynman1-4.pdfEin Objekt legt in einem gegebenen Zeitraum die Bahn AB zurück. Nach dem Prinzip der kleinsten Wirkung (genauer: Prinzip der stationären Wirkung) sind kleine Variationen dieser Bahn möglich. Es kann also auch eine Zitterbewegung um AB herum geben, bei der die physikalische Größe der Wirkung unverändert bleibt. Die theoretische Zitterbewegung kann man dann idealisiert durch ihre Komponenten darstellen. Daraus ergibt sich einerseits die Strecke CD, die parallel zu AB verläuft und in den physikalischen Eigenschaften, insbesondere der Wirkung, identisch ist. Alle Bewegungen quer dazu werden an den Enden zu AC und DB zusammengefasst. AC und DB sind entgegengesetzt gleich und heben sich daher gegenseitig auf. Das alles folgt aus dem Prinzip der stationären Wirkung.
Die Verschiebungen AC und DB werden als unendlich klein angenommen. Da CD mit AB identisch ist, kann von CD aus um ein weiteres unendlich kleines Stück weiter verschoben werden und dann immer so weiter. Und aus unendlich vielen unendlich kleinen Verschiebungen lässt sich dann eine beliebig große Strecke zusammensetzen. So folgt aus dem Prinzip der stationären Wirkung und den daraus abgeleiteten Eigenschaften eines physikalischen System in seiner unendlich nahen Umgebung, dass dessen physikalische Eigenschaften auch am anderen Ende des Universums gelten müssen.
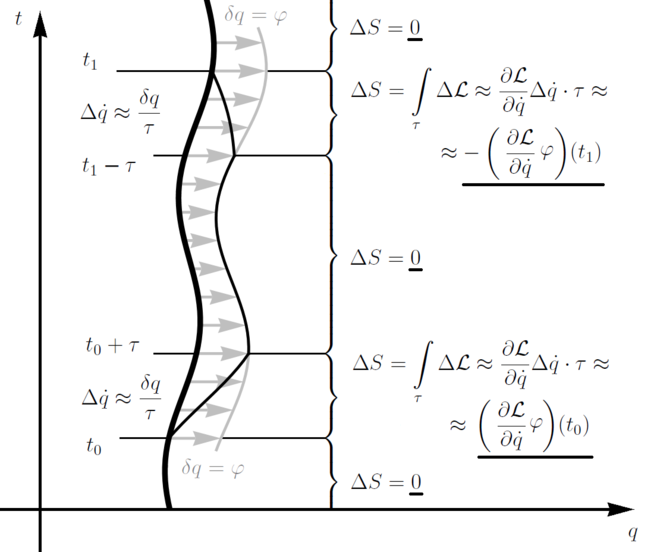
In einem Physikforum habe ich den Einwand gelesen, dass bei Feynman die Strecken AC und DB waagerecht verlaufen, was einem unendlich großen Impuls entsprechen würde. Diese Strecken repräsentieren jedoch Komponenten der Wirkung und in Bezug darauf entspricht waagerecht dem Impuls, während senkrecht für die Energie stehen würde. Im englischen Eintrag der Wikipedia für das Noether-Theorem wurde das vorsorglich abgeändert, siehe zweites Bild. Die abgeschrägten Schlenker muss man sich allerdings unendlich kurz vorstellen, weshalb es letztlich keinen Unterschied bedeutet.
In der Abhandlung von Emmy Noether geht es weit darüber hinaus um physikalische Systeme, die aus beliebig vielen Objekten bestehen können. Und es kann sich in beliebig vielen Dimensionen abspielen. In der Anwendung üblicherweise Flächen, die von Feldern durchdrungen werden. Und in den Gleichungen dürfen beliebig viele Potenzen und Ableitungen vorkommen. Sie war wirklich sehr gründlich.
Das Noether-Theorem war dann Jahrzehnte in der Versenkung verschwunden und kamm erst allmählich in die Wahrnehmung zurück, nachdem es 1971 ins Englische übersetzt worden war. Richard Feynman hat das Noether-Theorem bei seinem picture proof von 1965 also mit einiger Wahrscheinlichkeit gar nicht gekannt. Er hatte vermutlich eher das Pfadintegral im Sinn, das in seinem Vortrag allerdings ebenfalls nicht genannt wurde.
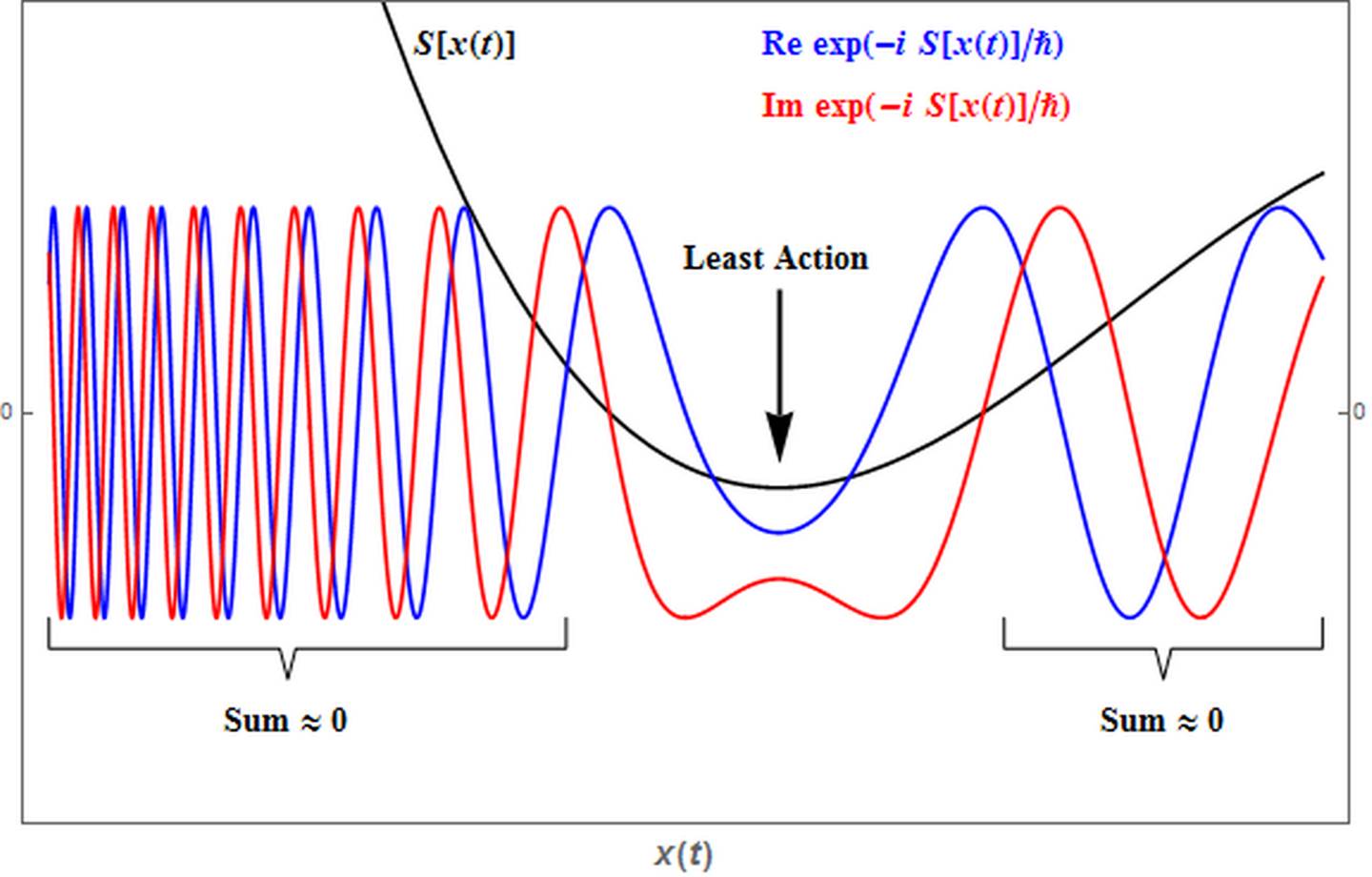
Für Feynman geht es nicht um die Abkoppelung von CD, sondern um die gesamte Bahn ACDB, die für ihn eine reale physikalische Bedeutung hat. Auch die physikalische Größe der Wirkung besitzt eine Wellennatur. Daraus folgt, dass Objekte theoretisch zunächst einmal beliebige Bahnen haben können. Je weiter abseits solche Bahnen liegen, umso mehr treffen dort unterschiedliche Phasen aufeinander, die sich gegenseitig auslöschen, siehe drittes Bild. Was übrig bleibt ist dann ein Bündel von Bahnen um den klassischen Weg eines Objektes herum. Dieses Bündel von Bahnen entspricht im Sinne der Quantenphysik den Aufenthaltswahrscheinlichkeiten des Objektes.
Feynman stellt dazu fest, dass der Zusammenhang zwischen den Symmetrien und den Erhaltungsgrößen nur dann gegeben ist, wenn das Prinzip der stationären Wirkung gilt. Und dieses Prinzip gilt, weil es aus der Quantenphysik folgt.
realradioactiveman