Siegelschild schrieb:Könntest du bitte das mit der blauen Fläche in der Grafik etwas einfacher erklären? In der ersten Grafik kommt das blaue und in der zweiten geht es vom \color{#f0e0d0}\mathrm{E_{00}} Punkt nach links. Damit ist der Astronaut gemeint.
Gerne, doch kurz angemerkt, ich hatte ja gesagt, wir interessieren uns erstmal nur für die linke Grafik. Es macht Sinn - wirklich - erstmal die Dinge zu verstehen, die ich gerade erkläre, die anderen Dinge erkläre ich dann danach. Wenn die ersten verstanden sind. Das baut alles aufeinander auf. Es macht auch wenig Sinn in der Schule das Mathematikbuch zu Beginn gleich zum Ende zu blättern und sich zu fragen, was das nur alles ist. Ich sage nicht, dass ich das nicht so gemacht habe, aber ist ja meine Baustelle.
Neugierde ist dennoch total toll und bewundernswert.
Dann blättern wir eben mal vor, ich zeige jetzt beide großen Grafiken, aus denen die beiden einzelnen Teile geschnitten sind. Ich sage aber hier schon, es wird Euch erschlagen. Und ich beantworte danach auch einfach und klar Deine Fragen.
Nur damit es hier schon gesagt wurdeWer richtig gut aufpasst, wird erkennen, dass in der Grafik für die Bezeichnung der Zeitachse \color{#f0e0d0}\mathrm{ct} steht. Man würde aber wohl nur \color{#f0e0d0}\mathrm{t}
erwarten. Man macht das aber oft, dass man die Zeit noch eben mit der Lichtgeschwindigkeit \color{#f0e0d0}\mathrm{v = c = 1} multipliziert.
Wenn man eine Geschwindigkeit mit einer Zeit multipliziert, bekommt man eine Länge.
Also, wenn wenn ein Photon sich genau 1 s lange mit c bewegt, dann hat es die Strecke 1 Ls zurückgelegt (eine Lichtsekunde). Warum die das machen? Damit man dann auf beiden Achsen nur Abstände hat, beide Einheiten sind dann auf der Raum- und auf der Zeitachse eben 'Ls' also Lichtsekunde.
Und ja, bei mir in der Grafik steht aber für die Zeit weiter hin 's' und nicht 'Ls' und das müsste schon richtig Ls sein. Ich habe die Grafik über die Zeit entwickelt, es sind wohl über 50 einzelne Ebenen und auch viele Ebenen-Gruppen. Als kleiner Monk und Perfektionist braucht es viel Zeit, die ganzen Einheiten noch mal anzupassen, würde wohl 5 h dauern. Und, es könnte nun auch einige verwirren, warum die Zeit nun mit einer Längeneinheit angegeben wird. Da kann ich einfacher sagen, ignoriert mal das c bei ct, das ist eh nur 1.
Ich schreibe das hier nur, damit nicht nachher wer kommt, und sagt, ja die Einheiten sind ja alle bei den Zeiten falsch, ja ist richtig, weiß ich.
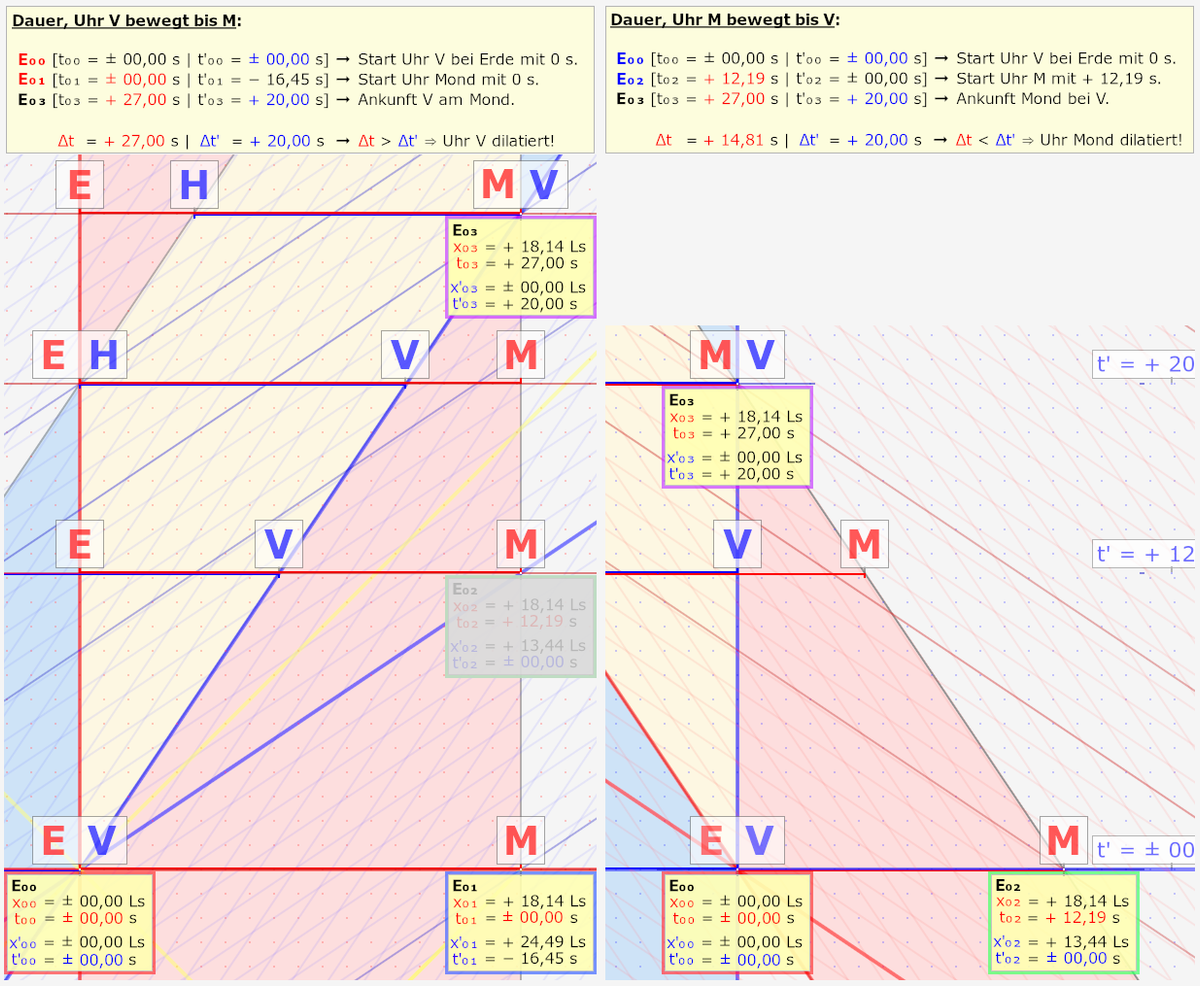
Wenn man die Grafiken richtig groß sehen will, rechte Maustaste und dann "Bild in in neuem Tab öffnen". Wir sehen ein Minkowski-Diagramm. Das gezeigte Ruhesystem ist
\color{#f0d0e0}\mathrm{S} und in rot. Wir haben nach oben die
\color{#f0d0e0}\mathrm{ct} Achse für die Zeit und von links nach rechts die
\color{#f0d0e0}\mathrm{x} Achse.
Sucht - wer es denn will - zuerst mal das Koordinatenkreuz, die Achsen, der Nullpunkt/Ursprung ist ja schon mit
\color{#f0e0d0}\mathrm{E_{00}} bekannt. Das Treffen von einer Uhr auf der Erde
\color{#f0d0e0}\mathrm{E} und einer Uhr
\color{#d0e0f0}\mathrm{V} vorne im Raumschiff.
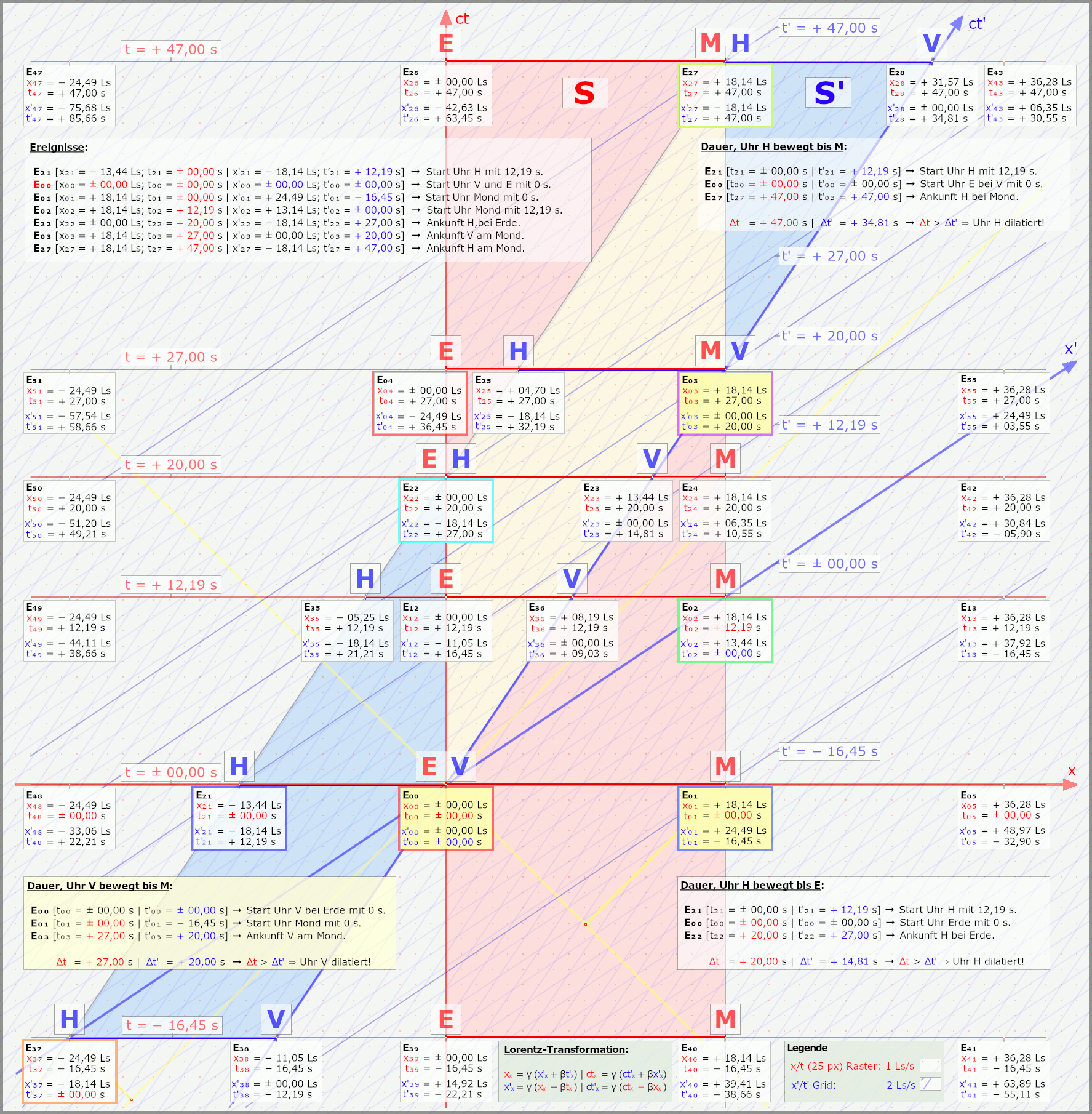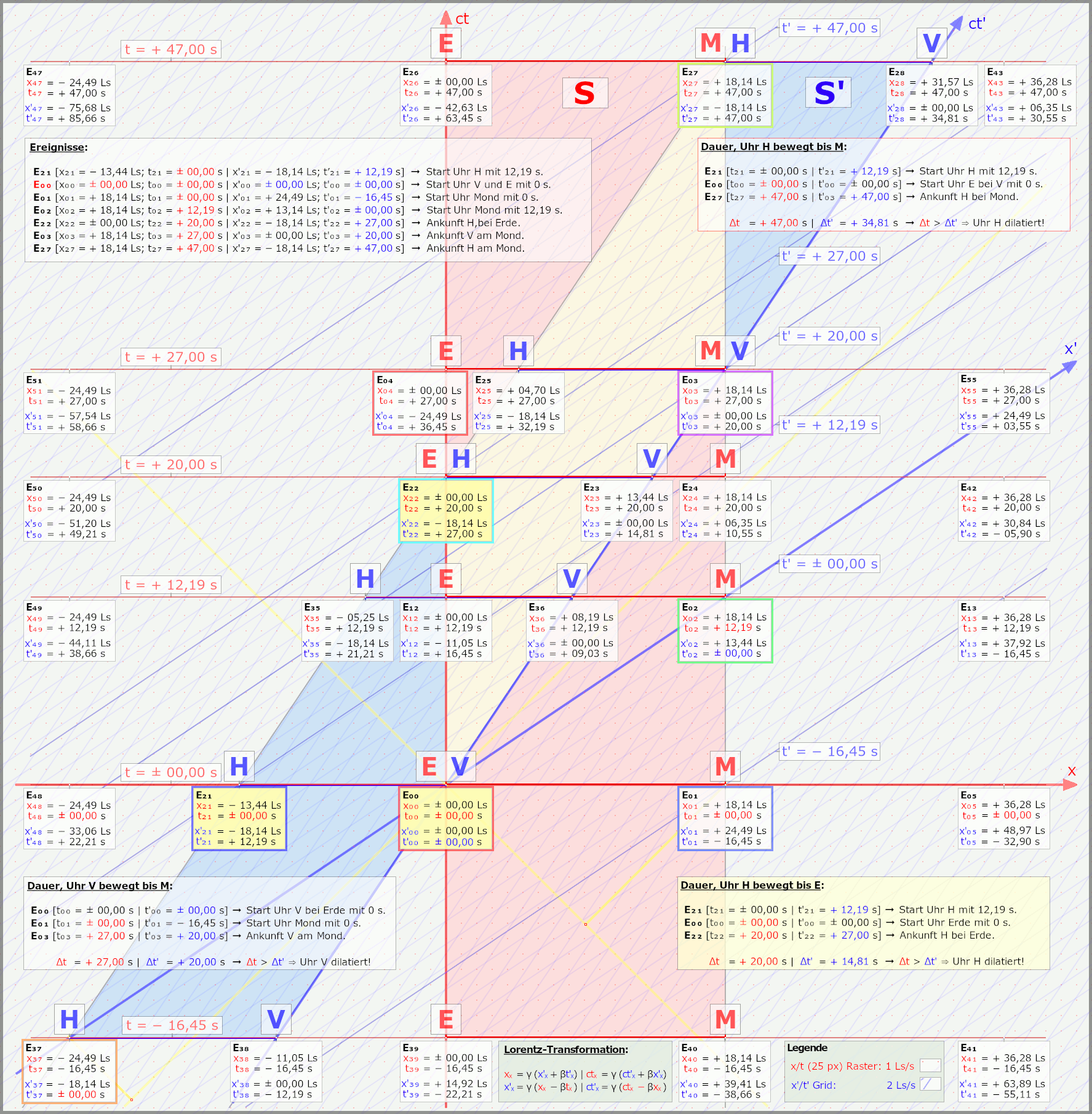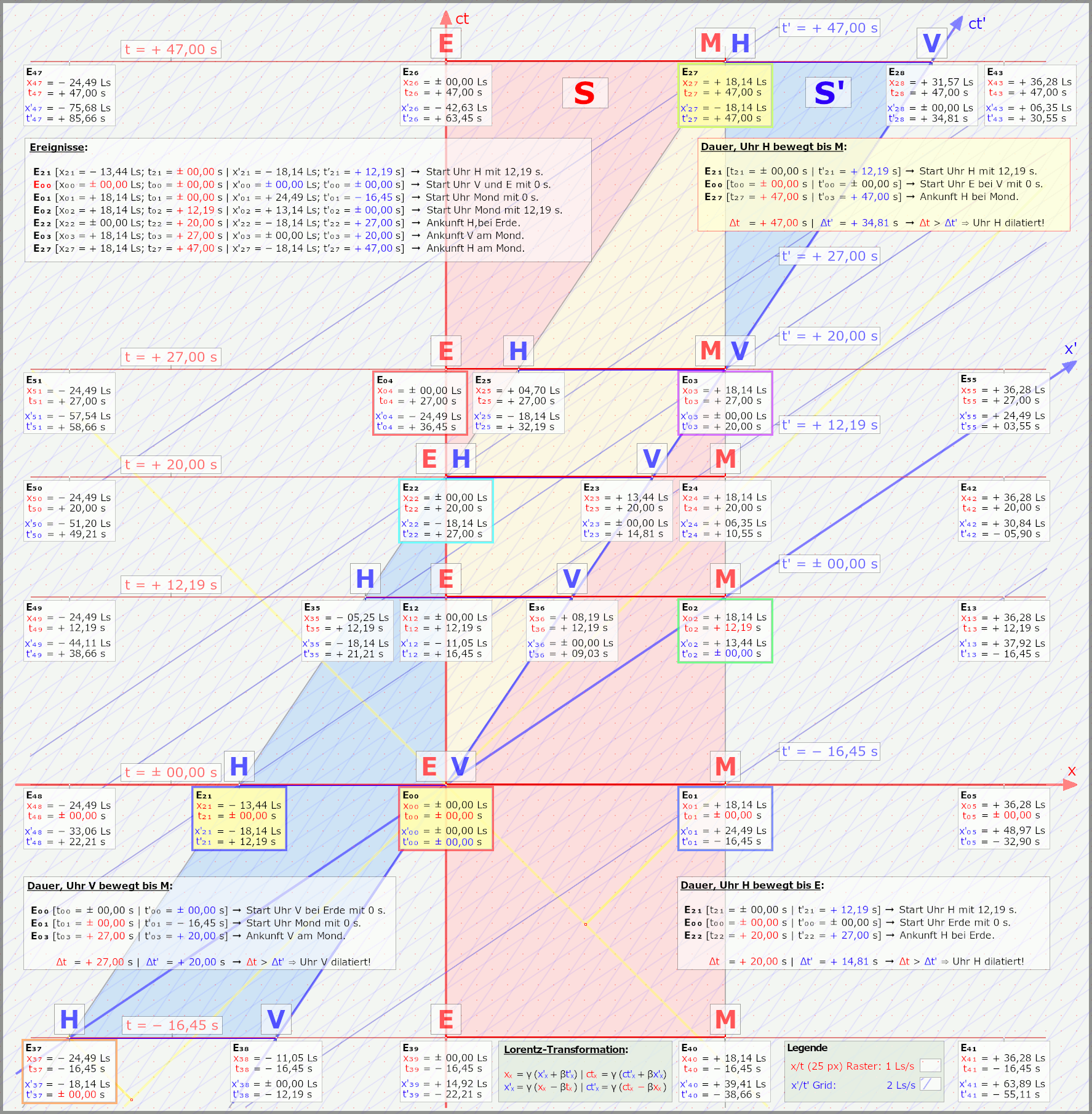Nun zu der blauen und roten Fläche:
Bleiben wir mal bei
\color{#f0e0d0}\mathrm{E_{00}}, da sehen wir die Erde zum Zeitpunkt
\color{#f0d0e0}\mathrm{t_{00}=0\hspace{1px}s}. Liegt damit genau auf der
\color{#f0d0e0}\mathrm{x} und
\color{#f0d0e0}\mathrm{ct} Achse, die sich an diesem Raumzeitpunkt schneiden. Verfolgen wir nun die Erde durch die Zeit auf der
\color{#f0d0e0}\mathrm{ct} Achse nach oben.
Wir sehen weitere Ereignisse, da ist eben wer auf der Erde bei einer Uhr und liest die immer ab:
\color{#f0e0d0}\mathrm{E_{00}}\hspace{1px}:\hspace{5px} \color{#f0d0e0}\mathrm{t_{00}=\pm 00,00\hspace{1px}s}\hspace{5px}|\hspace{5px}\mathrm{x_{00}=\pm 00,00\hspace{1px}Ls} \color{#f0e0d0}\mathrm{E_{12}}\hspace{1px}:\hspace{5px} \color{#f0d0e0}\mathrm{t_{12}=+ 12,19\hspace{1px}s}\hspace{5px}|\hspace{5px}\mathrm{x_{12}=\pm 00,00\hspace{1px}Ls} \color{#f0e0d0}\mathrm{E_{22}}\hspace{1px}:\hspace{5px} \color{#f0d0e0}\mathrm{t_{22}=+ 20,00\hspace{1px}s}\hspace{5px}|\hspace{5px}\mathrm{x_{22}=\pm 00,00\hspace{1px}Ls} \color{#f0e0d0}\mathrm{E_{04}}\hspace{1px}:\hspace{5px} \color{#f0d0e0}\mathrm{t_{04}=+ 27,00\hspace{1px}s}\hspace{5px}|\hspace{5px}\mathrm{x_{04}=\pm 00,00\hspace{1px}Ls} \color{#f0e0d0}\mathrm{E_{26}}\hspace{1px}:\hspace{5px} \color{#f0d0e0}\mathrm{t_{26}=+ 47,00\hspace{1px}s}\hspace{5px}|\hspace{5px}\mathrm{x_{26}=\pm 00,00\hspace{1px}Ls} Die Uhr wird fünfmal abgelesen. Und wir sehen,
die Erde ruht. Sie bewegt sich nicht und bleibt immer am selben Ort, genau auf der Zeitachse.
Darum gilt für alle Ereignisse auf der Erde:
\color{#f0d0e0}\mathrm{x_{xx}=\pm 00,00\hspace{1px}Ls}
Nun schauen wir mal weiter nach rechts da haben wir den Mond (M):
\color{#f0e0d0}\mathrm{E_{02}}\hspace{1px}:\hspace{5px} \color{#f0d0e0}\mathrm{t_{02}=\pm 00,00\hspace{1px}s}\hspace{5px}|\hspace{5px}\mathrm{x_{02}=+ 18,14\hspace{1px}Ls} Auch der wandert durch die Zeit, bewegt sich parallel zur Erde nach oben. Wir finden da weitere Ereignisse, die immer gleichzeitig zu denen auf der Erde sind. Ich schreibe nun nicht auch noch alle diese Ereignisse hier hin.
Erde und Mond bewegen sich auf
Weltlinie. Und Beide Linien spannen nun eine Weltfläche auf, in rot dargestellt.
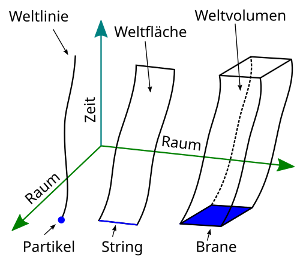
Die blaue Fläche (in meinen Grafiken) ist auch eine Weltfläche, die zwischen Uhr hinten (H) und Uhr vorne (V) der bewegten Rakete liegt. Wir betrachten eigentlich ja auch erstmal nur V auf der Reise von der Erde zum Mond.
Die beiden Weltflächen schneiden sich nun und die Schnittfläche habe ich leicht gelb dargestellt.
Siegelschild schrieb:Aber warum kommt die in dem linken Koordinatensystem von links zu Punkt \color{#f0e0d0}\mathrm{E_{00}}?
Nun sollte es klar sein, weil die Rakete im System bewegt ist, und damit ist die Weltfläche auch schräge. Beide Weltflächen treffen bei
\color{#f0e0d0}\mathrm{E_{00}} aufeinander.
Und wer jetzt auch noch die andere Grafik für die Szene sehen will, wo die Rakete in S' ruht und Erde/Mond bewegt sind, der klickt hier
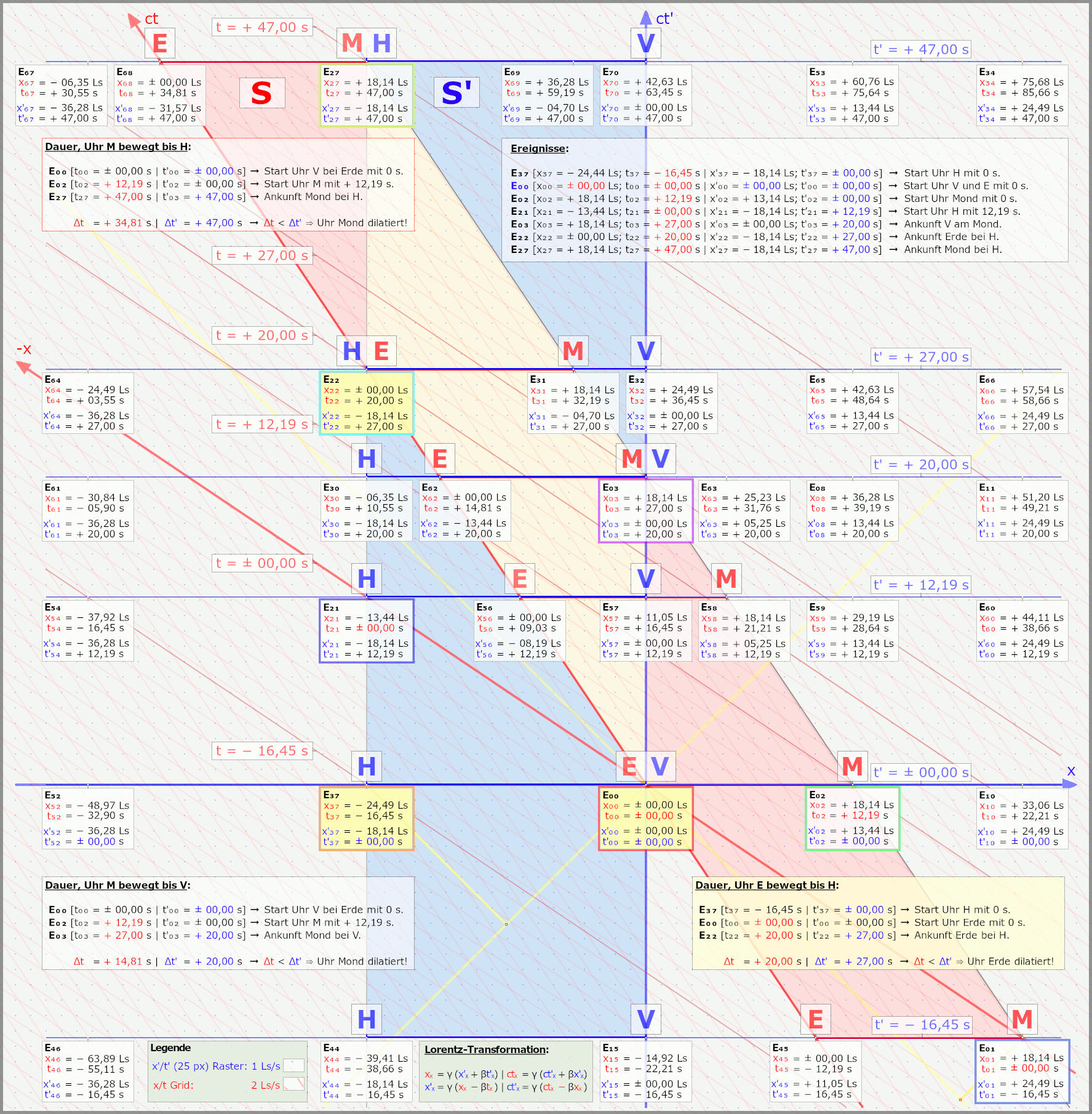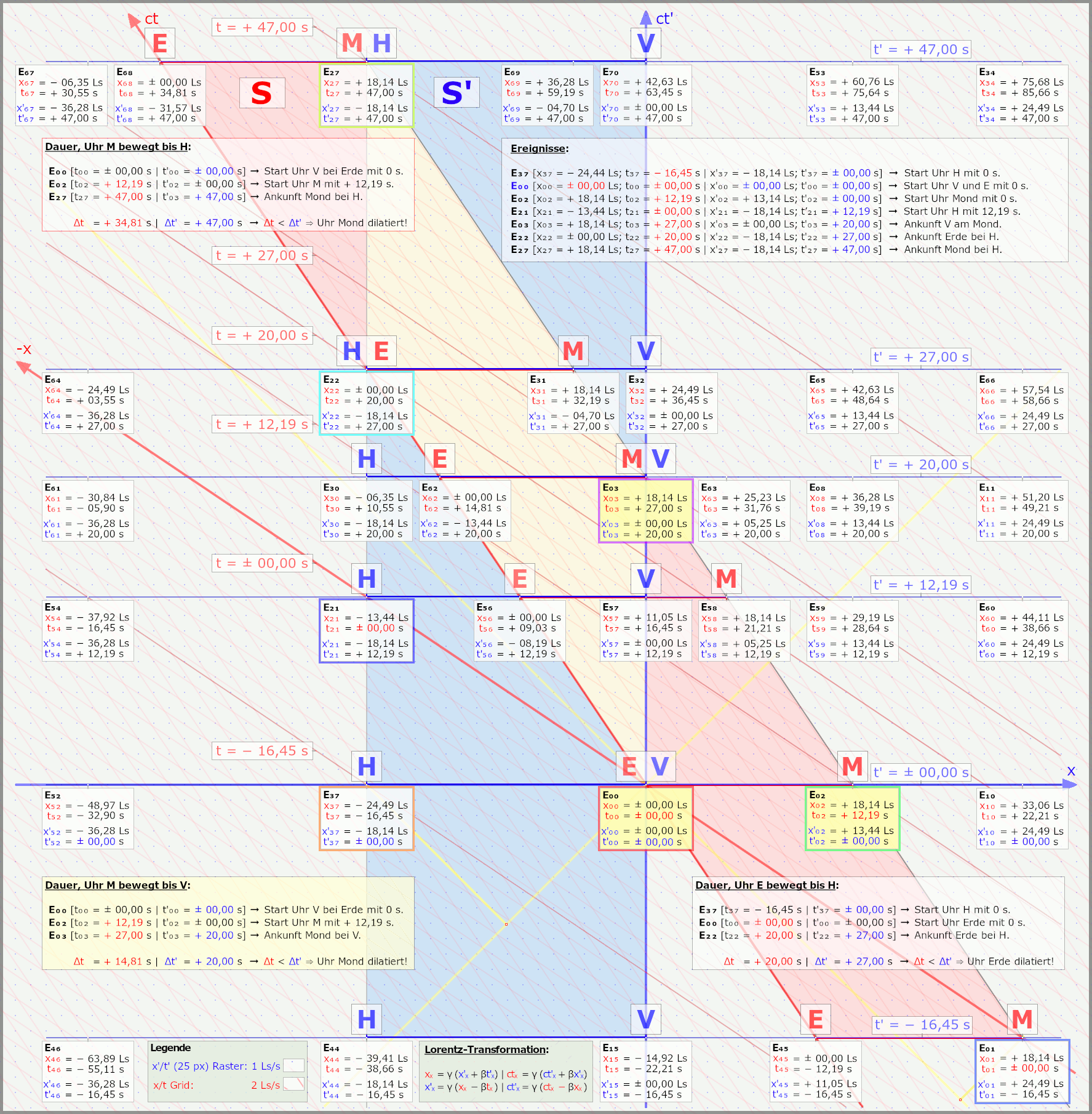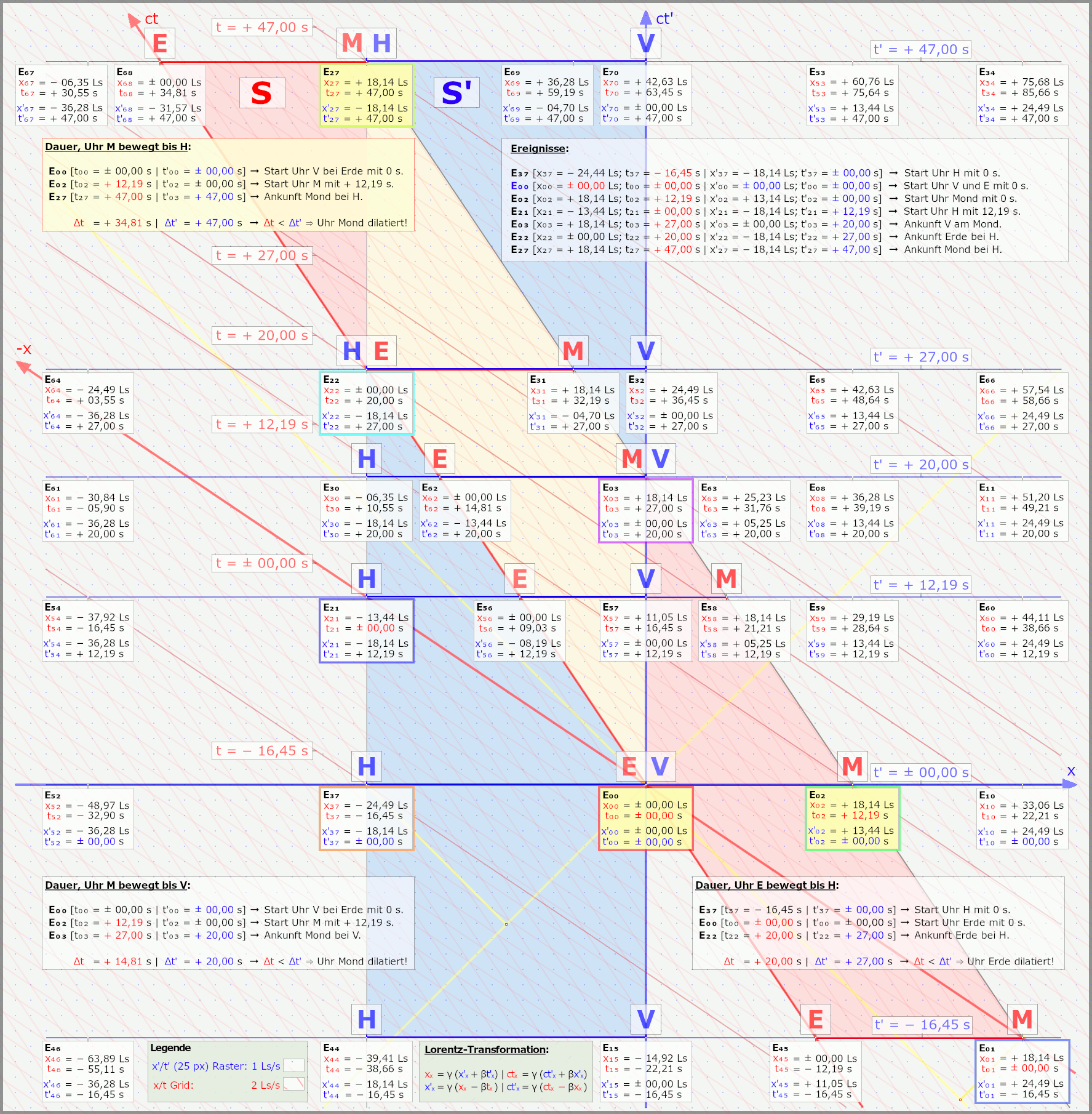
Ich werde die Grafik hier aber erstmal nicht weiter im Spoiler erklären, nur für jene, die gerne mehr sehen wollen und selber grübeln.
Siegelschild schrieb:Und warum geht die blaue Fläche in dem zweiten Koordinatensystem der selben Grafik auf der rechten Seite nach links?
Weil die rechte Seite ein Ausschnitt aus dem anderen Minkowski-Diagramm ist, das im Spoiler, und wenn Du da schaust, siehst Du, es geht da gar nicht nach links, sieht nur so aus, wegen der Schnittfläche. In Wirklichkeit geht die blaue Fläche da einfach nur gerade nach oben, ist eben die Weltfläche vom Raumschiff und das ruht im Ruhesystem S', das System mit den blauen Koordinatenachsen.
Siegelschild schrieb:Eine letzte Sache muss ich noch zu deiner 3.en Grafik sagen. Es wäre vielleicht hilfreich gewesen einen dicken schwarzen Strich zwischen beide Koordinatensystemen zu setzen. Ich hatte erst beim 4.en lesen des Textes verstanden das es 2 Koordinatensysteme in einer Grafik sind.
Ja, man hätte beide Teile besser abgrenzen können. Und so oder so, sind es in jedem Teil zwei Koordinatensysteme. Wir haben immer zwei, ein rotes und ein blaues Koordinatensystem. Links ist das System S in rot das Ruhesystem und System S' in blau das bewegte System. und auf der rechten Seite ist das blaue System S' das Ruhesystem und S das rote System eben bewegt. Und ja, die Achsen von dem bewegten System sind jeweils immer schräge, auf der linken Seite die beiden fetten blauen Linien, auf der einen bewegt sich ja auch V. Das ist die Zeitachse im blauen System.
Siegelschild schrieb:Noch eine Frage zum Abschluss. Warum um alles in der Welt steckst du 240 h in eine Grafik?
Ich musste mich eh mit den Funktionen des Grafikprogramms auseinandersetzten und ich habe ja nicht nur die Grafik erstellt, sondern dazu auch eine Tabelle in Excel mit allen Koordinatenwerten berechnet. Es begann mit dem Uhrenparadoxon, ich wollte mein Verständnis der SRT noch mal wieder vertiefen. Ich habe solche Grafiken - nicht ganz so professionell - schon mal vor über zehn Jahren erstellt, auch hier im Forum gezeigt.
Wenn man nicht als Physiker arbeitet, sondern als Berater und Programmierer, dann geht Verständnis der Dinge in zehn Jahren schon mal verloren. Ich möchte aber nichts verlieren, sondern mein Wissen und Verständnis erweitern, also aufbauen. Dafür braucht es Training.
So, noch mal ganz allgemein:
Ich befürchte, das hier war etwas zu viel, aber ich wurde ja gefragt. Es wäre einfacher, wirklich, wenn wir die Dinge so angehen, wie ich sie erkläre. Ich hatte ja
nur zwei einfache Ereignisse benannt, nur die linke Seite auf der Grafik, nur die Reise der Uhr V von der Erde zum Mond. Die geht über eine bestimmte Strecke und dauert eine bestimmte Zeit.
Und weil ich nicht einfach nur Zeit verbrennen will, in dem ich neue Grafiken erstelle, und dann hier nur den Alleinunterhalter mache, hab ich eine Grafik genommen, die ich eben schon habe. Wenn man sich das anschaut, was ich beschrieben habe, dann passt das schon. Es bringt kaum was, es sei denn man ist Autodidakt und bringt sich alles selbst bei, hier die Dinge anzugehen, die noch gar nicht erklärt sind. Wenn dann lasst uns das doch Schritt für Schritt machen.
Auch
wäre ich echt erfreut, wenn Ihr Euch mal den Fragen widmet, ist keine Pflichtübung, aber
es wäre für mich hilfreich, damit ich weiß, was verstanden wurde, und was noch nicht.
Und ich werde hier nicht weiter machen, wenn es kein gemeinsames Projekt wird.
Ich habe die Grafiken, wenn es hier was bringt, ich kann alles ausblenden, nur die Achsen anzeigen, nur das einer oder andere Ereignis, nur die Weltflächen, nur Erde, nur Mond. Ich kann eine Animation machen, wo das Diagramm Stück für Stück aufgebaut wird. Nur mach ich das nicht einfach aus Langweile, ich mache mir gerne auch die Arbeit, und investiere die Zeit, wenn es etwas bringt.
