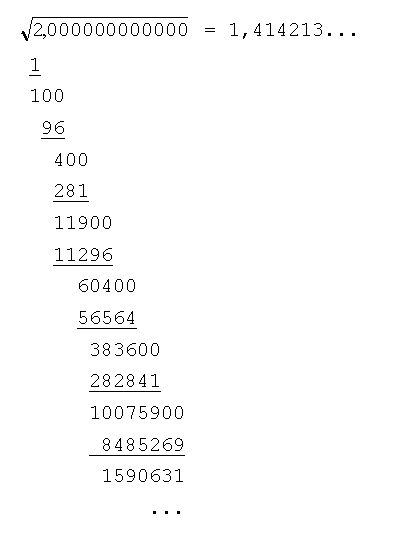PI..unedlich und nicht periodisch!..oder?

@Cyrk
"Ja, ich meinte ob man sie überhaupt ziehen kann..."

Natuelrich kann man sie ziehen

Die Wurzel aus 2 kann man auch ziehen

"Weil die Würzel von 2 geht ja z.B nich ohne einen gerundeten Wert zu verwenden..."

Natuelrich geht die ohne einen Gerundeten Wert.

Nur wenn du Wurzel 2 als dezimalzahl schreibst dann musst du wohl nach irgendeiner endlichesn Stelenzahl aufhoeren sprich runden.

Und das trifft genau so auch auf die wurzel der anderen von dir genannten zahlen zu...

Im Uebrigen

Wirzel(20)= 2 mal Wurzel (5)
Wurzel(200)= 10 mal Wurzel (2)
Wurzel (2000)= 50 mal Wurzel(5)
usw usw

Also wenn man Wurzel 2 und Wurzel 5 kennt kann man die anderen sehr bequem durch Multiplikation berechnen...

@Bright2

Ja, das wusste ich... aber die Frage ist nun ob es Das selbe Problem auch bei den Zahlen 20, 200, 2000, 20000 [...] gibt

Also ob die Zahl die aus Wurzel-20 rauskommt ebenfalls unendlich ist

@Bright2
Als Bruch ganzer zahlen... Meine Fresse sonst kannst du auch gleich alles als sich selbst durch eins schreiben und frohlocken das es jetzt ein Bruch ist

@JPhys

Ja genau das mein ich...
Ich will sie in Dezimalen haben...

Es ist doch so das man aus z.B. 5 eine exakte Wurzel (In Dezimalstellen) ziehen kann, auch wenn sie angenommen 130 Stellen nach dem Komma hatt.

Doch bei der 2 Gibt es doch das Problem das ähnlich wie bei Pi die Nachkommastellen niemals enden, oder ?!

@Cyrk
Es ist doch so das man aus z.B. 5 eine exakte Wurzel (In Dezimalstellen) ziehen kann, auch wenn sie angenommen 130 Stellen nach dem Komma hatt.

Nein ist es nicht

Die Wurzel einer ganzen Zahl ist entweder ganz oder irrational...

Wenn es bei einer ganzen Zahl auch nur eine Nachkomma stelle gibt gibt es unendlich viele von ihnen...

"Doch bei der 2 Gibt es doch das Problem das ähnlich wie bei Pi die Nachkommastellen niemals enden, oder ?!"

Wie gesagt das Problem gibt es bei JEDER ganzen zahl die nicht eine quadratzahl ist
mit quadratzahl meine ich 1 ,4 ,9 , 16 usw

Warum ist das so?

Weil das quadrat einer zahl mit x Nachkomma stellen immer 2x nachkomma stellen hat.
Durch Quadrieren wird die Zahl von Nachkommastellen NIE kleiner....

Wieso? ganz einfach die letzte NAchkommastelle koennte eine 1 sein dann wird das Quadrat eine 1 in der 2x ten Stelle habe
sie koennte eine 2 sein dann wir das quadrat eine 4 in der 2x ten stelle haben

bei einer 3 eine 9
bei einer 4 eine 6
bei einer 5 eine 5
bei einer 6 eine 6
bei einer 7 eine 9
bei einer 8 eine 4
bei einer 9 eine1

Du siehst in keinem Fall einen 0

Also hat jedes Audrat einer zahl mit endlich vielen NAchkommer Stellen immer mehr NAchkomma stellen als die Zahl ...

Probier es aus einfach mal schriftlich multiplizieren du wirst feststellen fuer die letzte NAchkommastelle spielt nur die letzte Anchkommastelle eine Role sonst nichts...

OK die Rechtschreibung wir langsam ein Problem

Also hat jedes Quadrat einer Zahl mit endlich vielen Nachkommastellen immer mehr Nachkomma stellen als die Zahl ...

Probier es aus einfach mal schriftlich multiplizieren und du wirst feststellen, fuer die letzte Nachkommastelle spielt nur die letzte Nachkommastelle eine Rolle. Sonst nichts...

@Cyrk

Cyrk schrieb:Doch bei der 2 Gibt es doch das Problem das ähnlich wie bei Pi die Nachkommastellen niemals enden, oder ?!

Hier liegt die Problematik in den Nachkommastellen.
Bei 1, 414213... mal sich selbst, ergibt dies 1,999998409369
Dieser hintere Teil ...8409369 wird in die Teilbarkeit wohl unendlich bleiben.

@JPhys
*grübel... Ja stimmt eigendlich...
Ich bin denoch davon überzeugt dass das irgen ein Rätsel ist das man aus 2 nicht eine vollständige Wurzel (Zahl mit x nachkommastellen) ziehen kann, ohne x nur in Zahlen zu definieren

Wenn das bei alle auser den Quadratzahlen so ist, wo ist dan die Besonderheit?

Mom ich suchs mal kurz raus, muss doch hier i wo sein =/
(Saustall lässt grüßen ^^)




@DonFungi
Das mein ich, bei anderen Zahlen ist es doch nicht so oder ? also ich mein jetzt nichtquadratzahlen...

Puhhh ich finds nich...
Es stand in einem -Welt der Wunder- Heft

Kann mir jem helfen ?

@Cyrk


Ich glaub da steht wo was von Dezimal und Bruch. Was darüber hinaus geht, hat da so seine Probleme.

Bei Wurzel 2 gilt als Rechnung „ mal sich selbst“ eine andere Regel.
Da 1 x 1 = 1 ergibt, wird somit das gewünschte Ergebnis nicht erzielt.
Wir wollen ja das Quadrat und nicht ne Multiplikation..

Wir können im Kopf selbst nachvollziehen wie sich 1, 1 / 1,2 / 1,3 ........ mal sich selbst verhält.


1,2 x 1,2 = 1,44
1,3 x 1,3 = 1,69 usw.

1,1 x 1,1 = 1,1 + 0,11 = 1,21

1,2 x 1,2 = 1,2 + (2 x 0,12) = 1,44
1,3 x 1,3 = 1,3 + (3 x 0,13) = 1,69
1,4 x 1,4 = 1,4 + (4 x 0,14) = 1,96

1,5 x 1,5 = 1,5 + (5 x 0,15) = 2,25 = zu viel!

Und so wird es logisch weshalb Wurzel 2 eine 1,4 ...... Stelle ist.


Es ist halt so in der Mathematik, dass es Zahlen gibt, die beim Teilen zu keinem Ende kommen.

Bei Pi wird sich der Errechnete Kreis, rein Mathematisch gesehen, nicht schliessen. Aber wir können uns annähern und sagen, hier ist Schluss.